【第14回】元東大教員から学ぶリアルタイムシステム「Deferrable Server」

こういった私から学べます．

前回を読んでいない方はこちらからどうぞ．

リアルタイムシステムの記事一覧はこちらからどうぞ．

リアルタイムシステムで使われているリアルタイムOSは，主にC言語で書かれています．

私にC言語の無料相談をしたいあなたは，公式LINE「ChishiroのC言語」の友だち追加をお願い致します．

私のキャパシティもあり，一定数に達したら終了しますので，今すぐ追加しましょう！

独学が難しいあなたは，元東大教員がおすすめするC言語を学べるオンラインプログラミングスクール5社で自分に合うスクールを見つけましょう．後悔はさせません！

Deferrable Server（DS）

Deferrable Server（DS）はStrosninderらにより提案された非周期タスクの平均の応答性を向上する非周期サーバです．

PSと同様に，DSは非周期タスクを実行するために（普通は最高優先度を持つ）周期タスクを生成します．

しかし，PSとは異なり，非周期サーバの呼び出し時に非周期タスクがない場合，DSは非周期サーバの容量を保持します．

サーバの容量は周期の終わりまで保持します．

なので，サーバの容量が枯渇しない限り，非周期タスクはいつでも同じ非周期サーバの優先度で実行できます．

非周期サーバの周期の最初に，サーバの容量は満タンまで補給されます．

\(\tau_i\)：タスク	\(C_i\)：最悪実行時間	\(T_i\)：周期
\(\tau_1\)	1	4
\(\tau_2\)	2	6
\(\tau_s\)（非周期タスク）	2（非周期サーバの容量）	5（非周期サーバの周期）

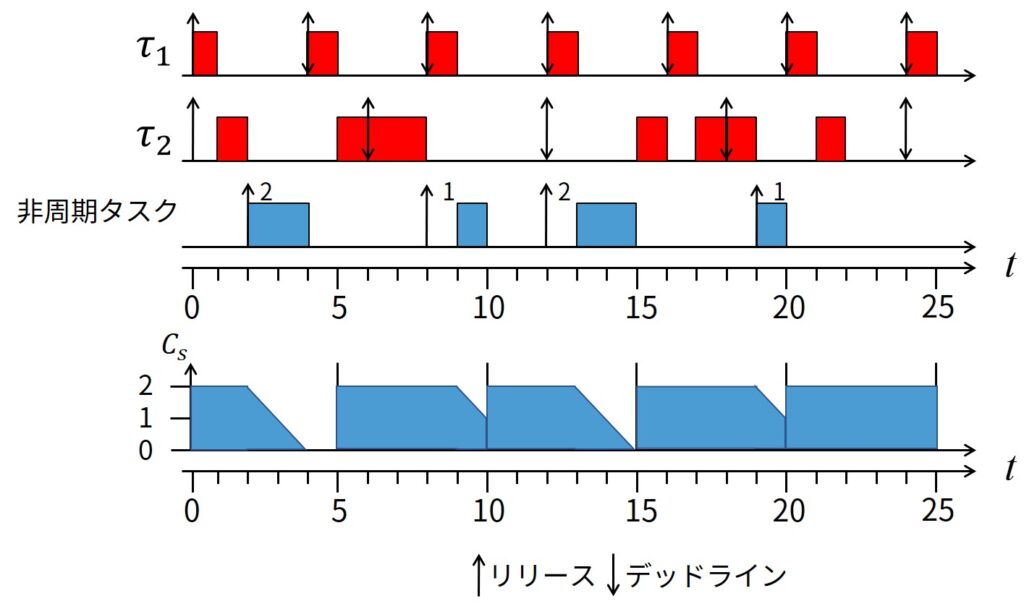
上図に示すように，DSは前回のPSの場合と同じ周期タスクセットと非周期サーバ（\(C_s=2\)，\(T_s=5\)）を持ちます．

• 時刻\(t=1\)：タスク\(\tau_1\)が終了した時に非周期タスクがない場合，CPUはタスク\(\tau_2\)を割り当てます．
  しかし，DSの容量は周期タスクに使わずに，将来の非周期タスクに使われます．
• 時刻\(t=2\)：最初の非周期タスクが到着し，すぐにその非周期タスクを実行開始します．
• 時刻\(t=4\)：容量がなくなり，次の周期まで実行できなくなります．
• 時刻\(t=5\)：容量\(C_s\)は満タンまで補給され，次の到着まで待機します．
• 時刻\(t=8\)：次の非周期タスクが到着しましたが，最高優先度の\(\tau_1\)が実行中なのですぐには実行できずに待機状態になります．

DSは必要になるまで容量を確保しているので，PSより非周期タスクの応答性が高くなります．

より短い応答時間は周期タスクの中でDSを最高優先度にすれば実現できます．

\(\tau_i\)：タスク	\(C_i\)：最悪実行時間	\(T_i\)：周期
\(\tau_1\)	2	8
\(\tau_2\)	3	10
\(\tau_s\)（非周期タスク）	2（非周期サーバの容量）	6（非周期サーバの周期）

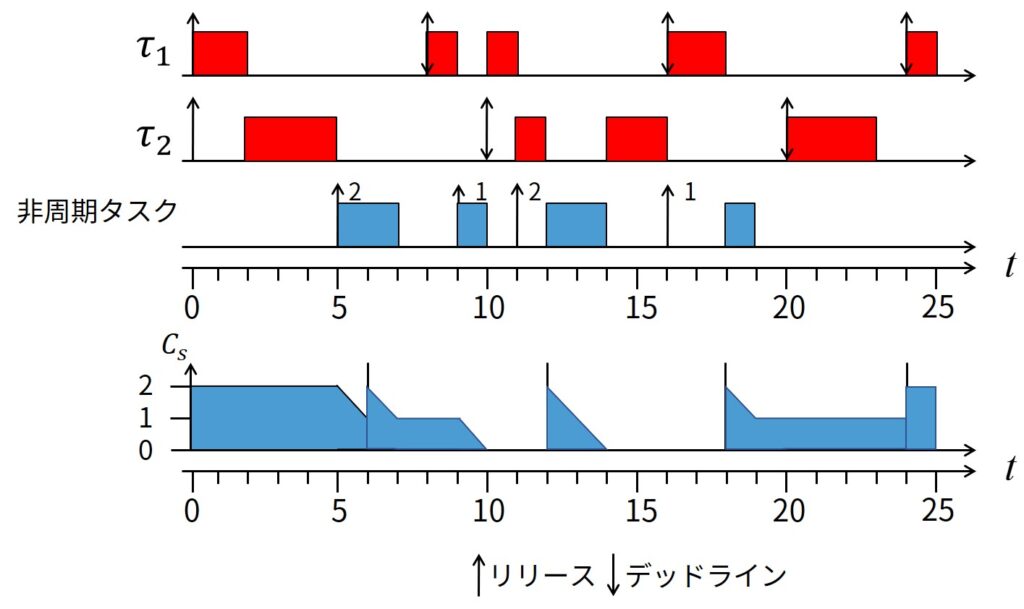
上図にDSが高優先度の例を示します．

• 時刻\(t=9\)：\(C_s=0\)かつ\(T_s < T_1\)なので，2番目の非周期タスクはタスク\(\tau_1\)をプリエンプションします．
• 時刻\(t=10\)：2番目の非周期の実行が完了し，容量を完全に消費して空になります．
• 時刻\(t=11\)：3番目の非周期タスクが到着した時，容量\(C_s=0\)なので，次の非周期サーバの周期の最初（時刻\(t=12\)）まで遅延します．
• 時刻\(t=12\)：非周期サーバの周期の最初になり容量が満タンまで補給されたので，2番目の非周期タスクを実行します．
• 時刻\(t=14\)：3番目の非周期の実行が完了し，容量を完全に消費して空になります．
• 時刻\(t=16\)：4番目の非周期タスクが到着しますが，容量が空なので，同様の処理になります．

DSのスケジュール可能性解析

RMに関連するあらゆるスケジュール可能性解析では，周期タスクは自分自身で実行を延期できないという想定に基づいています．

しかし，最高優先度タスクが実行可能状態であれば実行しなければなりません．（「想定A5：タスクはI/O処理などで自分自身を中断できない．」）

DSはこの想定を違反していることが簡単にわかります．

実際，先程のDSが高優先度の例の図では，DSは最高優先度で実行可能状態にも関わらず，時刻\(t=0\)で実行していません．

DSは時刻\(t=5\)に最初の非周期タスクが到着するまで実行を遅延します．

もし周期タスクがすぐに実行できた時に実行を遅延した場合，低優先度タスクはタスクセットがスケジュール可能な場合でもデッドラインミスする可能性があります．

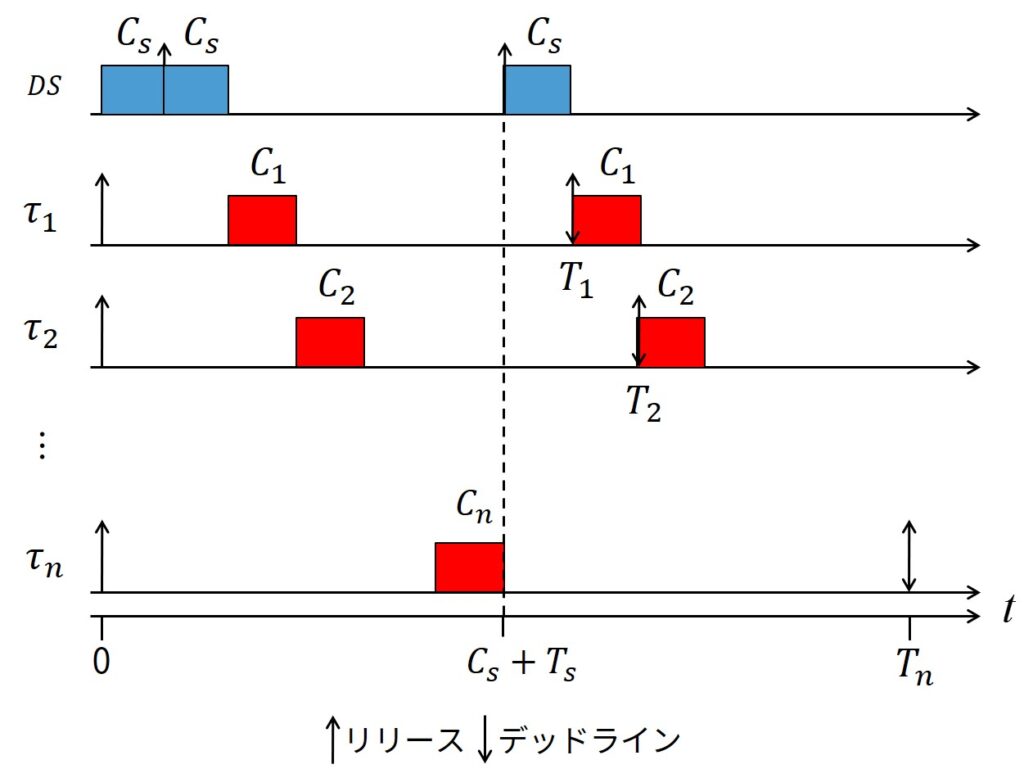
同じ周期と最悪実行時間で周期タスクとDSの実行を比較する例を示します．

この例の周期タスクセットは2つのタスクから構成されています．

タスク\(\tau_1\)，\(\tau_2\)は同じ最悪実行時間（\(C_1=C_2=2\)）を持ち，異なる周期（\(T_1=4\)，\(T_2=5\)）を持ちます．

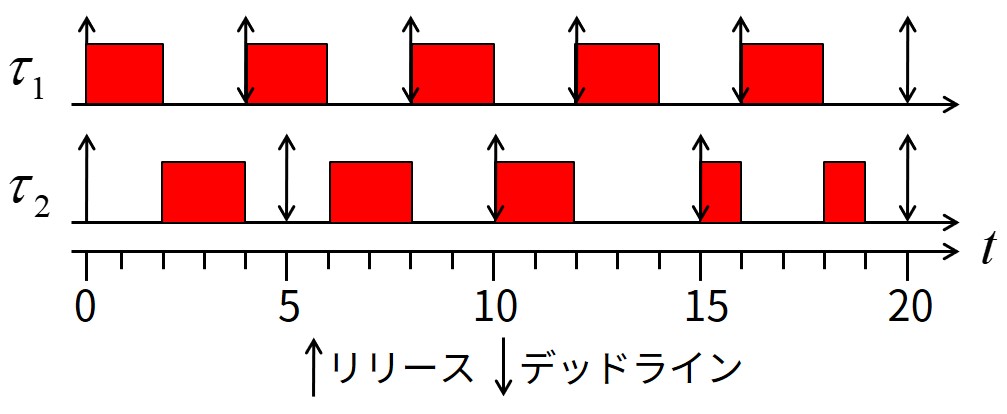
上図は，2つのタスクがRMでスケジュール可能な場合です．

しかし，もしタスク\(\tau_1\)が同じ周期と最悪実行時間（容量）を持つDSに置き換えた場合，低優先度タスク\(\tau_2\)は非周期タスクの到着の順序に依存してデッドラインミスする可能性があります．

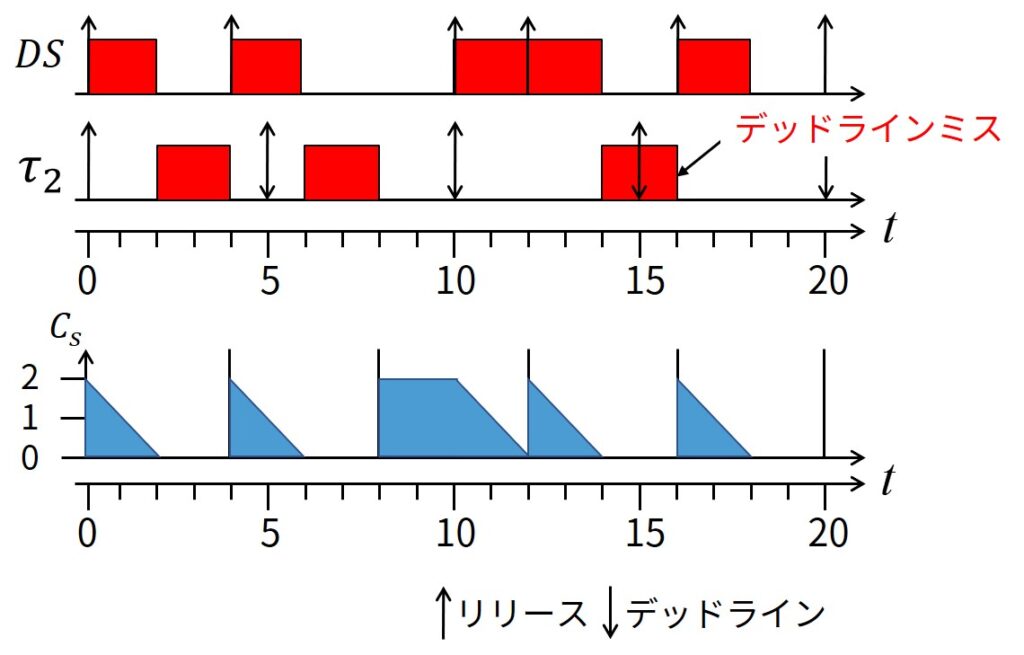
上図は非周期タスクの到着順序により時刻\(t=15\)でタスク\(\tau_2\)がデッドラインミスした例です．

時刻\(t=8\)にDSは普通の周期タスクのように実行せずに，将来の非周期タスクのための容量を確保することが原因で発生しています．

区間\([10, 14)\)における2つの連続した非周期タスクの実行は，タスク\(\tau_2\)をこの区間で実行することを妨害し，デッドラインミスを引き起こします．

DSの侵略的な振る舞いは周期タスクセットのスケジュール可能上限の低下を引き起こします．

DSにおける非周期タスクのCPU利用率

DSを用いた周期タスクセットのスケジュール可能性解析はRMの\(U_{lub}\)の算出における同じ想定から派生します．

\(n\)タスクのスケジュール可能上限の算出を簡略化するためには，タスク間の最悪の関係を決定し，最悪ケースのモデルに対する下限を算出します．

\(n\)個の周期タスクのセット\(\tau_1, ..., \tau_n\)が周期の短い順にソートされ，最高優先度にDSがある場合を考慮します．

周期タスクの最悪条件は，RMのスケジュール可能性解析から派生して，\(T_1 < T_n < 2T_1\)になります．

しかし，DSにより，最悪ケースの派生はRMより複雑になり，3つのケースを解析する必要があります．

分かりやすくするために，1ケースのみ解析します．

より一般的には，DSは最高優先度タスクの周期内に3回実行するかもしれません．

DSが周期の終わりまで実行を遅延し，次の周期の最初に実行する時に，この状況が発生します．

この状況では，下図に示すように，以下のタスクのパラメータでCPUをフル活用します．

\begin{cases}
C_s &=& T_1 - (T_s + C_s) = (T_1 - T_s)/2 \\
C_1 &=& T_2 - T_1 \\
C_2 &=& T_3 - T_2 \\
... \\
C_{n-1} &=& T_n - T_{n-1} \\
C_n &=& T_s - C_s = \sum_{i=1}^{n-1} C_i = (3T_s + T_1 - 2T_n)/2
\end{cases}

合計CPU利用率\(U\)は下式になります．

\begin{eqnarray}
U &=& \frac{C_s}{T_s} + \frac{C_1}{T_1} + ... + \frac{C_n}{T_n} \\
&=& U_s + \frac{T_2 - T_1}{T_1} + ... + \frac{T_n - T_{n-1}}{T_{n-1}} + \frac{3T_s + T_1 - 2T_n}{2T_n} \\
&=& U_s + \frac{T_2}{T_1} + ... + \frac{T_n}{T_{n-1}} + \left( \frac{3T_s}{2T_1} + \frac{1}{2} \right) \frac{T_1}{T_n} - n
\end{eqnarray}

以下を定義します．

\begin{cases}
R_s &=& T_1 / T_s \\
R_i &=& T_{i+1} / T_i \\
K &=& (3T_s/T_1 + 1) / 2
\end{cases}

ここで，以下の関係が導出できます．

$$R_1 R_2 ... R_{n-1} = \frac{T_n}{T_1} $$

CPU利用率は以下のように書き換えられます．

$$U = U_s + \sum_{i=1}^{n-1} R_i + \frac{K}{R_1 R_2 ... R_{n-1}} - n$$

RMで利用した手法により，\(R_i (i = 1, ..., n-1)\)に対して\(U\)を最小化します．

$$\frac{\partial U}{\partial R_i} = 1 - \frac{K}{R_i^2 \left( \prod_{j \neq i}^{n-1} R_j \right)} $$

\(P=R_1 R_2 ... R_{n-1}\)と定義した場合，\(U\)は以下の条件を満たす場合に最小値になります．

\begin{cases}
R_1 P &=& K \\
R_2 P &=& K \\
... \\
R_{n-1} P &=& K
\end{cases}

すなわち，全ての\(R_i\)が同じ値の時になります．

$$R_1 = R_2 = ... = R_{n-1} = K^{1/n}$$

\(U\)から\(R_1, ..., R_{n-1}\)を除去すると，以下になります．

\begin{eqnarray}
U_{lub} - U_s &=& (n - 1) K^{1/n} + \frac{K}{K^{(1-1/n})} - n \\
&=& nK^{1/n} - K^{1/n} + K^{1/n} - n \\
&=& n(K^{1/n} - 1)
\end{eqnarray}

すなわち，\(U_{lub}\)は以下になります．

$$U_{lub} = U_s + n(K^{1/n} - 1)$$

また，\(U_s\)は以下になります．

$$U_s = \frac{C_s}{T_s} = \frac{T_1 - T_s}{2T_s} = \frac{R_s - 1}{2} $$

\(R_s\)は以下になります．

$$R_s = 2(U_s + 1)$$

\(K\)は下式に書き換えられます．

$$K = \left( \frac{3}{2R_s} + \frac{1}{2} \right) = \frac{U_s + 2}{2U_s + 1} $$

したがって，\(U_{lub}\)は下式になります．

$$U_{lub} = U_s + n \left[ \left( \frac{U_s + 2}{2U_s + 1} \right) ^{1/n} - 1 \right]$$

極限\( n \to \infty\)を取ると，\(U_s\)の関数のスケジュール可能上限は下式になります．

$$ \lim_{n \to \infty} U_{lub} = U_s + \ln{\left( \frac{U_s + 2}{2U_s + 1} \right) } \tag{14.1} $$

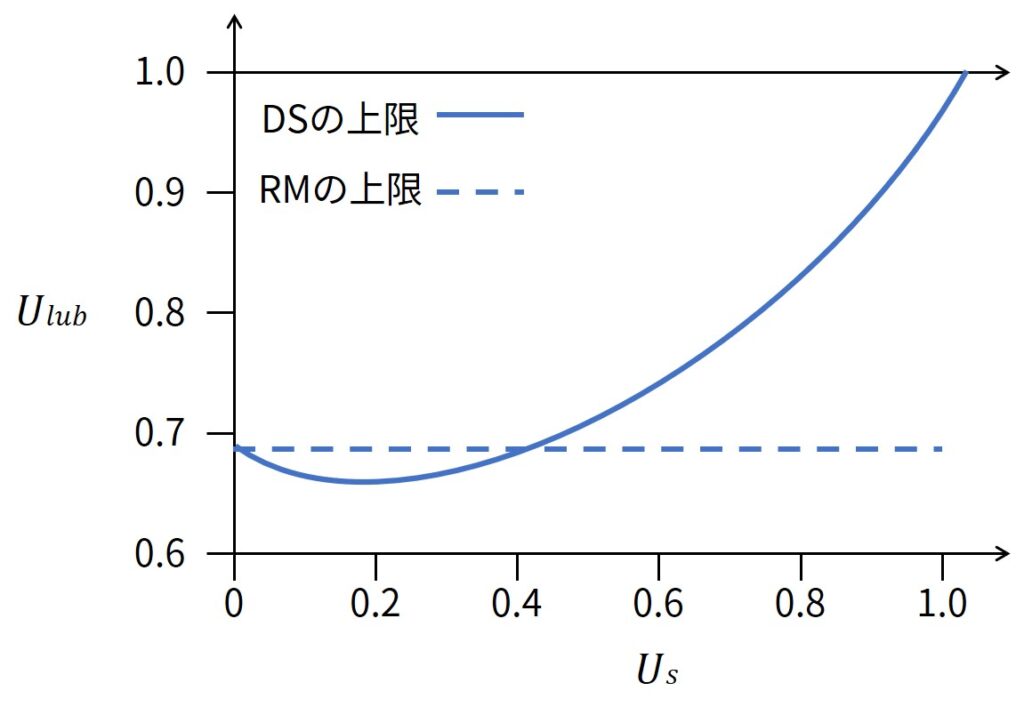
上図に式\((14.1)\)における\(U_s\)の関数を示します．

比較のために，RMのスケジュール可能上限を掲載します．

\(U_s < 0.4\)の場合，DSはRMよりスケジュール可能上限が低くなります．

\(U_s > 0.4\)の場合，DSはRMよりスケジュール可能上限が高くなります．

\(U_s\)に関する式\((14.1)\)から派生して，\(U_{lub}\)の最小値を算出すると以下になります．

$$\frac{\partial U_{lub}}{\partial U_s} = 1 + \frac{(2U_s + 1)}{(U_s + 2)} \frac{(2U_s + 1) - 2(U_s + 2)}{(2U_s + 1)^2} = \frac{2U_s^2 + 5U_s - 1}{(U_s + 2)(2U_s + 1)} $$

\(U_{lub}\)は\(2U_s^2 + 5U_s - 1 = 0\)の時に最小値になります．

※参考までに，2次方程式\(a x^2 + bx + c = 0 \ \ \ (a \neq 0)\)の解は下式になります．

$$x = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a}$$

2次方程式の解の公式を利用すると，\(2U_s^2 + 5U_s - 1 = 0\)の解は下式になります．

$$U_s = \frac{-5 \pm \sqrt{5^2 - 4 \times 2 \times -1}}{4} = \frac{-5 \pm \sqrt{33}}{4} $$

ここで，\(U_s > 0\)なので，\(U_s\)の解は下式になります．

$$U_s = \frac{-5 + \sqrt{33}}{4} $$

したがって，\(U_{lub}\)の最小値は\(U_{lub}^* \simeq 0.652\)になります．

まとめると，CPU利用率\(U_p\)の\(n\)個の周期タスクセットとCPU利用率\(U_s\)の非周期サーバDSがある場合，以下の条件を満たす場合に周期タスクセットのスケジュール可能性はRMで保証されます．

$$U_p \leq n \left( K^{1/n} - 1 \right)$$

ここで，\(K\)は下式になります．

$$K = \frac{U_s + 2}{2U_s + 1} $$

Hyperbolic Boundを利用する場合，DSを持つタスクセットのスケジュール可能性判定テストは以下になります．

$$\prod_{i=1}^n (U_i + 1) \leq \frac{U_s + 2}{2U_s + 1} \tag{14.2}$$

DSにおける最大CPU利用率

PSと同様の手法により，DSのCPU利用率の最大値\(U_s^{max}\)は式\((14.2)\)から簡単に算出できます．

式\((13.5)\)の\(P\)を利用して以下に書き換えられます．

$$P \leq \frac{U_s + 2}{2U_s + 1} $$

すなわち，\(U_s\)は以下になります．

$$U_s \leq \frac{2 - P}{2P - 1} $$

したがって，\(U_s^{max}\)は下式になります．

$$U_s^{max} = \frac{2 - P}{2P - 1} \tag{14.3}$$

\(T_s\)は最短周期\(T_1\)と同じになります．

優先度のタイブレーク方式はサーバの方が優先されますので，DSはRMにより最高優先度で実行されます．

最終的には\(C_s = U_s T_s\)になります．

DSにおける非周期タスクのスケジュール可能性解析

ファーム非周期ジョブのオンライン（実行時）でのリアルタイム性を保証するためには，DSが最高優先度のケースにおける最悪応答時間を見積もる必要があります．

DSは実行時間を保存するので，\(c_s (t)\)を時刻\(t\)における容量の値，\(J_a\)を最悪応答時間\(C_a\)，相対デッドライン\(D_a\)，到着時刻\(t=r_a\)の非周期ジョブとします．

また，時刻\(t=r_a\)には他の非周期タスクが実行を中断していないとします．

もし\(next(r_a) = \left\lceil r_a / T_s \right\rceil T_s\)が時刻\(r_a\)の後に次の非周期サーバが起動する時刻の場合，下図のように以下の2つのケースが発生します．

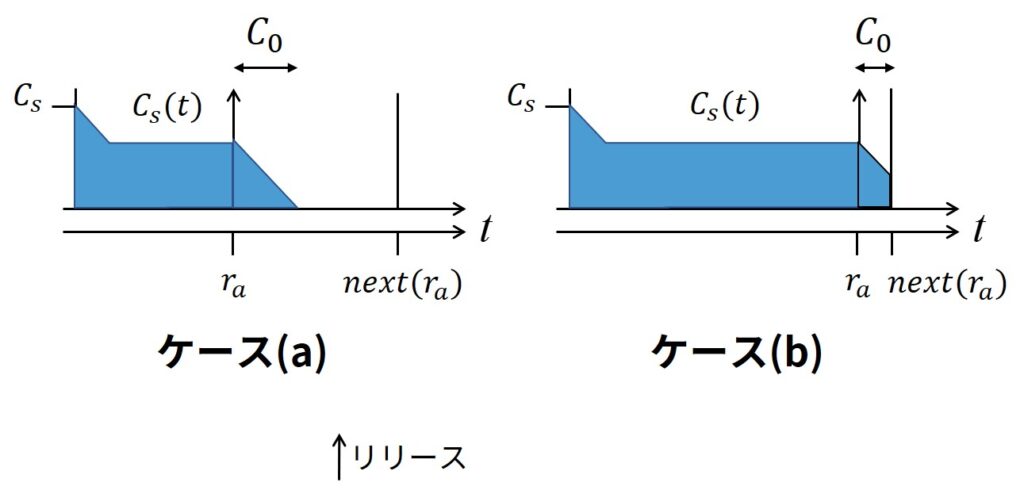
1. ケース(a)：\(c_s (t) \leq next(r_a) - r_a\)の場合．
   このケースでは，非周期サーバの容量が現在の周期で完全に空になります．
   \(J_a\)の部分\(C_0 = c_s(t)\)が現在の非周期サーバの周期で実行します．
2. ケース(b)：\(c_s (t) > next(r_a) - r_a\)の場合．
   このケースでは，周期は非周期サーバの容量が完全に空になる前に終了します．
   \(J_a\)の部分\(C_0 = next(r_a) - r_a\)が現在の非周期サーバの周期で実行します．

一般的には，現在の非周期サーバの周期で実行する部分\(C_0\)は以下と同じです．

$$C_0 = \min \{c_s(t), next(r_a) - r_a\}$$

PSと同じ表記を利用して，以下を定義します．

\begin{cases}
\Delta_a &=& next(r_a) - r_a \\
F_a &=& \left\lceil (C_a - C_0) / C_s \right\rceil - 1 \\
\delta_a &=& C_a - C_0 - F_a C_s
\end{cases}

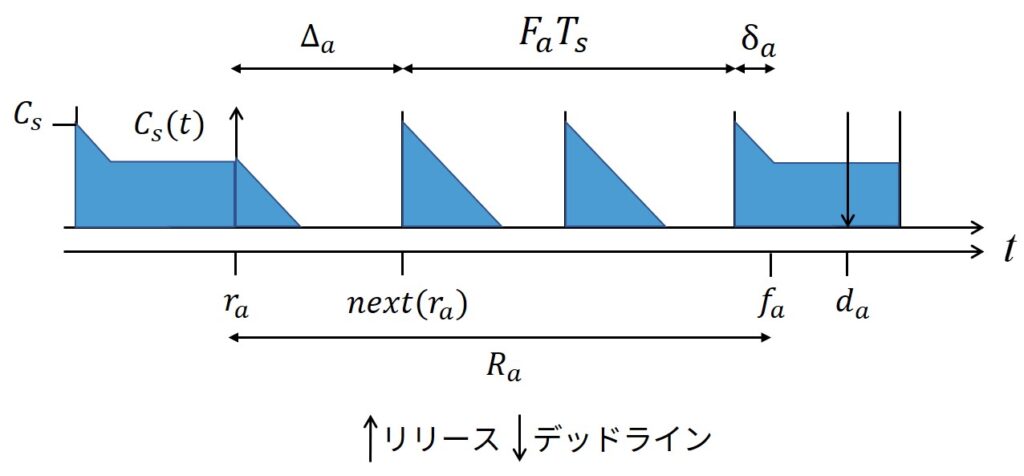
上図によると，ジョブ\(J_a\)の応答時間\(R_a\)は以下のように算出できます．

$$R_a = \Delta_a + F_a T_s + \delta_a$$

また，\(R_a\)は以下のように書き換えられます．

$$R_a = \Delta_a + C_a - C_0 + F_a (T_s - C_s) \tag{14.4}$$

式\((14.4)\)の期間\(F_a (T_s - C_s)\)は実行しない非周期サーバの間隔\(F_a\)と各々のサイズ\((T_s - C_s)\)の積による遅延となります．

そして，非周期ジョブのスケジュール可能性判定テストは，下式が成立する場合においてのみリアルタイム性を保証することができます．

$$R_a \leq D_a$$

まとめ

今回は，非周期サーバDeferrable Server（DS）を紹介しました．

具体的には，以下の内容を解説しました．

• DSの特徴（PSとは異なり，非周期サーバの呼び出し時に非周期タスクがない場合，DSは非周期サーバの容量を保持）
• DSのスケジュール可能性解析
• DSにおける最大CPU利用率
• DSにおける非周期タスクのスケジュール可能性解析

リアルタイムシステムで使われているリアルタイムOSは，主にC言語で書かれています．

私にC言語の無料相談をしたいあなたは，公式LINE「ChishiroのC言語」の友だち追加をお願い致します．

私のキャパシティもあり，一定数に達したら終了しますので，今すぐ追加しましょう！

独学が難しいあなたは，元東大教員がおすすめするC言語を学べるオンラインプログラミングスクール5社で自分に合うスクールを見つけましょう．後悔はさせません！

次回はこちらからどうぞ．