【第13回】元東大教員から学ぶリアルタイムシステム「Polling Server」

こういった私から学べます．

前回を読んでいない方はこちらからどうぞ．

リアルタイムシステムの記事一覧はこちらからどうぞ．

リアルタイムシステムで使われているリアルタイムOSは，主にC言語で書かれています．

私にC言語の無料相談をしたいあなたは，公式LINE「ChishiroのC言語」の友だち追加をお願い致します．

私のキャパシティもあり，一定数に達したら終了しますので，今すぐ追加しましょう！

独学が難しいあなたは，元東大教員がおすすめするC言語を学べるオンラインプログラミングスクール5社で自分に合うスクールを見つけましょう．後悔はさせません！

Polling Server（PS）

非周期タスクの平均応答時間は，非周期サーバを利用することでバックグラウンドスケジューリングより向上することができます．

すなわち，非周期タスクの目的は，非周期タスクを出来る限り速く処理できることです．

周期タスクのように，非周期サーバは周期\(T_s\)，サーバの容量（Capacity/Budget）\(C_s\)（周期タスクの最悪実行時間のようなもの）を持ちます．

一般的には，周期タスクと同じスケジューリング（例：RM，EDF）で非周期サーバをスケジュールします．

非周期サーバが起動した場合，非周期タスクを容量の範囲内で実行します．

非周期サーバ内の非周期タスクの実行順序は，周期タスクのスケジューリングに依存しません．

到着時刻，最悪実行時間，絶対デッドライン，他のパラメータにより非周期タスクをスケジュールします．

Polling Server（PS）は，周期\(T_s\)で起動し，容量\(C_s\)の範囲内で非周期タスクを実行する非周期サーバです．

もし非周期タスクがない場合，PSは次の周期の最初まで実行を延期します．

また，非周期タスク用に確保した非周期サーバの容量は解放し，その時間は周期タスクに割り当てられます．

もし非周期サーバの実行を延期した直後に非周期タスクが到着した場合，非周期サーバの次の周期の最初に容量を補充するまで非周期タスクの実行を待たなければなりません．

\(\tau_i\)：タスク	\(C_i\)：最悪実行時間	\(T_i\)：周期
\(\tau_1\)	1	4
\(\tau_2\)	2	6
\(\tau_s\)（非周期タスク）	2（非周期サーバの容量）	5（非周期サーバの周期）

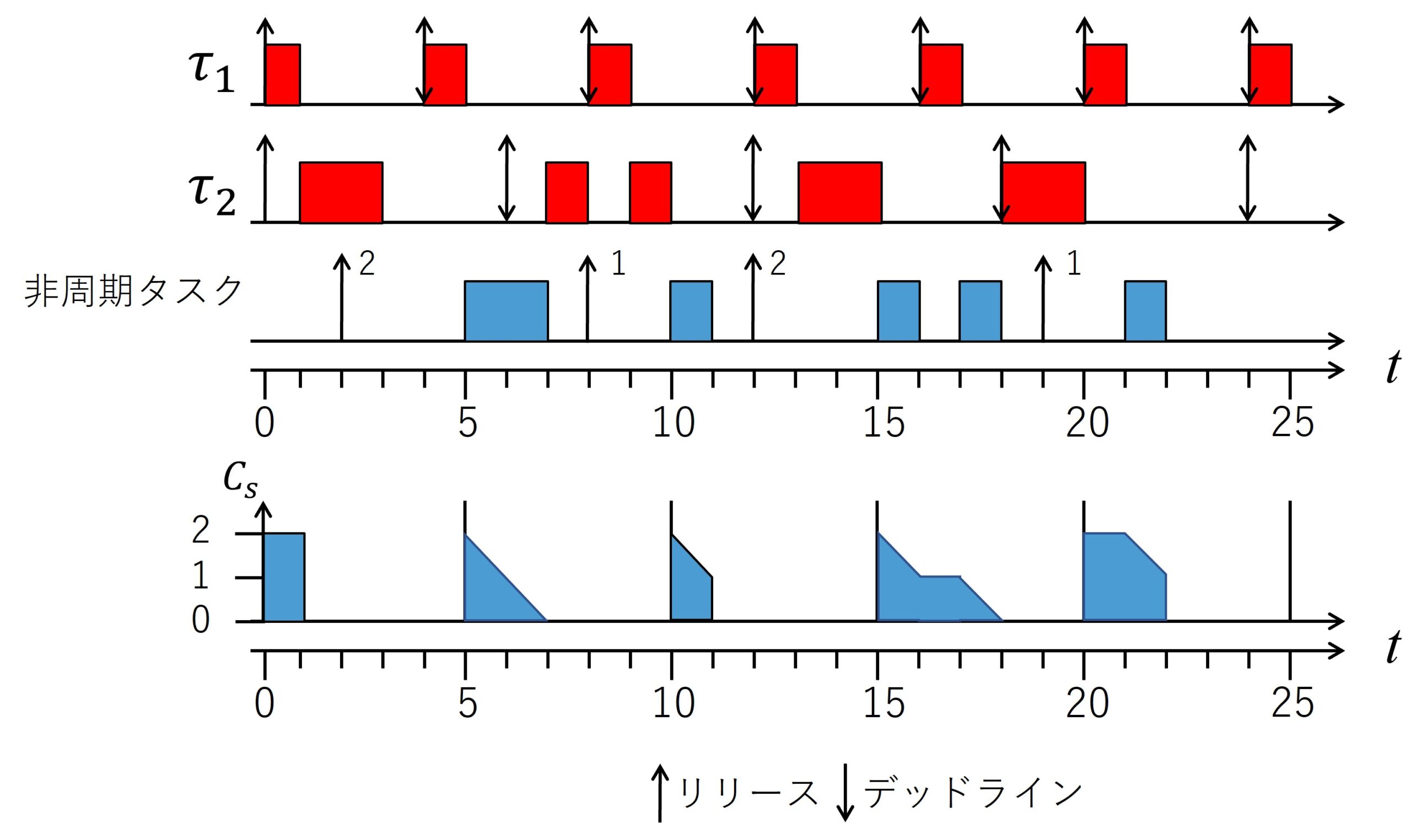
上表に周期タスクと非周期サーバのパラメータ，上図にRMでスケジュールされる非周期サーバPSの例を示します．

非周期タスクは3行目（\(\tau_2\)の下），非周期サーバPSの容量の関数は4行目に示します．

非周期タスクの矢印の右側にある数字は非周期タスクの実行時間を示します．

PSは，周期\(T_s = 5\)，容量\(C_s = 2\)なので，周期タスクと比較して中間の優先度（タスク\(\tau_1\)より低くタスク\(\tau_2\)より高い優先度）を持ちます．

• 時刻\(t=0\)：CPUはタスク\(\tau_1\)（RMスケジュールの最高優先度）を実行します．
• 時刻\(t=1\)：タスク\(\tau_1\)は実行終了し，CPUは非周期サーバを割り当てます．
  しかし，非周期タスクがないので，非周期サーバの実行は次の周期まで延期し，その容量は周期タスクに利用されます．
• 時刻\(t=2\)：非周期タスクが到着しますが，非周期サーバの実行は次の周期の開始時刻\(t=5\)まで実行を延期しなければなりません．
• 時刻\(t=5\)：非周期サーバの容量が満タン（\(C_s=2\)）まで供給し非周期タスクが終了するまで実行します．
  非周期サーバの容量が全部消費された場合，他の非周期タスクは，この周期では実行できません．
• 時刻\(t=10\)：次の非周期タスクは同様に実行しますが，サーバの容量は\(C_s=2\)の半分しか使わず，残り半分は非周期タスクがないので破棄します．
• 時刻\(t=16\)：3番目の非周期タスクはタスク\(\tau_1\)によりプリエンプションされますが，サーバの容量は保持したままになります．
• 時刻\(t=17\)：3番目の非周期タスクの残りを実行します．
• 時刻\(t=19\)：4番目の非周期タスクが到着しますが，非周期サーバの容量がないので次の周期の開始時刻\(t=20\)まで延期します．
• 時刻\(t=20\)：非周期サーバが起動しますが，タスク\(\tau_1\)の方が優先度が高いので，実行可能状態になります．
• 時刻\(t=21\)：タスク\(\tau_1\)が終了し，非周期サーバが非周期タスクを実行します．

PSのスケジュール可能性解析

RMによるハード周期タスクとPSによるソフト非周期タスクのスケジュール可能性を解析します．

周期タスクのスケジュール可能性解析は，周期実行するPSの干渉時間を算出することで保証することができます．

非周期サーバの干渉時間の最大値は，同じ周期タスクのパラメータ（周期\(T_s\)，最悪実行時間\(C_s\)）を持つ場合です．

実際，非周期サーバの周期\(T_s\)中に容量\(C_s\)分，非周期タスクを実行します．

PSのCPU利用率は\(U_s=C_s/T_s\)になり，\(n\)タスクで合計CPU利用率\(U_p\)の周期タスクセットと合せたスケジュール可能性解析は以下を満たす場合に保証できます．

$$U_p + U_s \leq U_{lub} (n + 1)$$

もし非周期サーバを含む周期タスクがRMによりスケジュールされる場合，スケジュール可能性判定テストは下式になります．

$$\sum_{i=1}^n \frac{C_i}{T_i} + \frac{C_s}{T_s} \leq (n + 1) [2^{1/(n+1)} - 1]$$

PSは複数個生成され，異なる非周期タスクを並行に実行できることに注意して下さい．

例えば，高優先度の非周期サーバは重要な非周期タスク，低優先度の非周期サーバは重要でない非周期タスクを扱うために利用できます．

一般的には，\(m\)個の非周期サーバと\(n\)個の周期タスクは以下の条件を満たす場合にRMでスケジュール可能になります．

$$U_p + \sum_{j=1}^m U_{s_j} \leq U_{lub} (n + m)$$

より正確なスケジュール可能性判定テストは，LiuとLaylandのスケジュール可能上限と同じ方法（PSを最高優先度タスクとみなす方法）で導出することができます．

算出を簡略化するためには，タスク間の最悪の関係を決定し，最悪ケースに対する下限を算出します．

\(n\)個の周期タスク\(\tau_1, ..., \tau_n\)は周期の短い順にソートされ，最高優先度でPSが動作するとします．

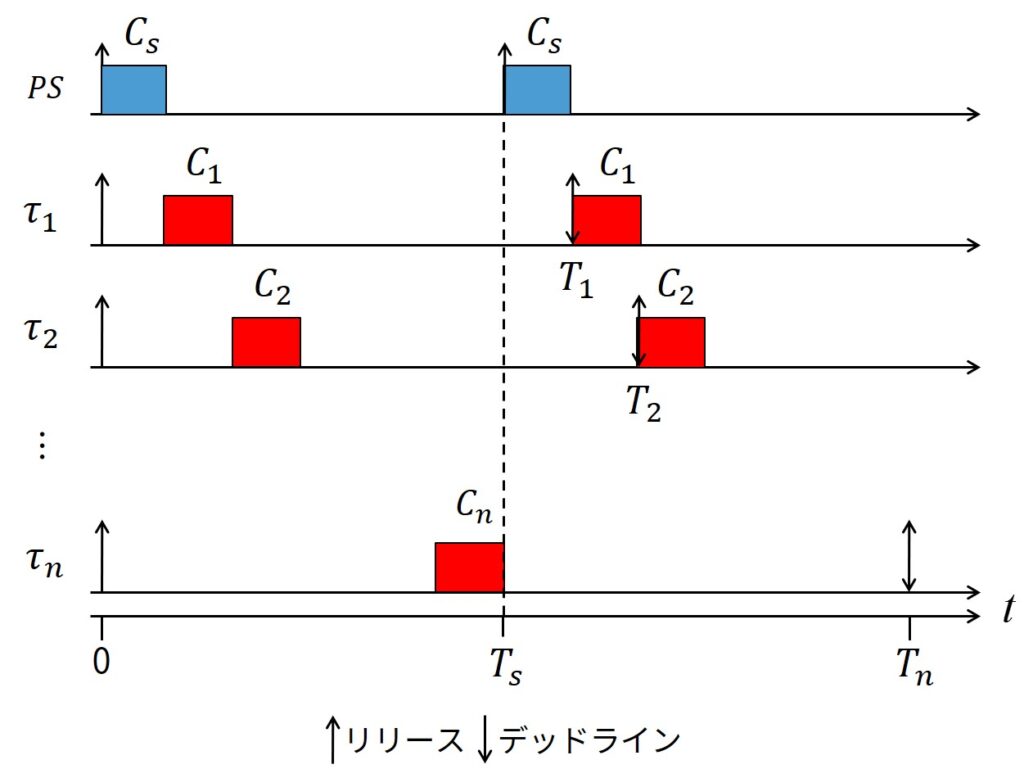
上図に周期タスクがCPUをフル活用する最悪ケースを示します．

周期タスクは以下のパラメータになります．

\begin{cases}
C_s = T_1 - T_s \\
C_1 = T_2 - T_1 \\
C_2 = T_3 - T_2 \\
... \\
C_{n-1} = T_n - T_{n-1} \\
C_n = T_s - C_s - \sum_{i=1}^{n-1} C_i = 2T_s - T_n
\end{cases}

合計CPU利用率は以下になります．

\begin{eqnarray}
U &=& \frac{C_s}{T_s} + \frac{C_1}{T_1} + ... + \frac{C_n}{T_n} \\
&=& U_s + \frac{T_2 - T_1}{T_1} + ... + \frac{T_n - T_{n-1}}{T_{n-1}} + \frac{2T_s - T_n}{T_n} \\
&=& U_s + \frac{T_2}{T_1} + ... + \frac{T_n}{T_{n-1}} + \left( \frac{2T_s}{T_1} \right) \frac{T_1}{T_n} - n
\end{eqnarray}

以下を定義します．

\begin{cases}
R_s &=& T_1/T_s \\
R_i &=& T_{i+1}/T_i \\
K &=& 2T_s/T_1 = 2/R_s
\end{cases}

以下が導出されます．

$$R_1 R_2 ... R_{n-1} = \frac{T_n}{T_1}$$

合計CPU利用率は以下になります．

$$U = U_s + \sum_{i=1}^{n-1} R_i + \frac{K}{R_1 R_2 ... R_{n-1}} - n$$

RMで利用した方法により，\(R_i (i = 1, ..., n-1)\)に対して\(U\)の最小値を算出します．

$$\frac{\partial U}{\partial R_i} = 1 - \frac{K}{R_i^2 \left(\prod_{j \neq i}^{n-1} R_j \right)}$$

\(P=R_1 R_2 ... R_{n-1}\)と定義すると，\(U\)は以下の時に最小値になります．

\begin{cases}
R_1 P = K \\
R_2 P = K \\
... \\
R_{n-1} P = K
\end{cases}

すなわち，全ての\(R_i\)が同じ値を持つ下式になります．

$$R_1 = R_2 = ... = R_{n-1} = K^{1/n}$$

\(R_i\)を消去すると，下式に展開されます．

\begin{eqnarray}
U_{lub} - U_s &=& (n - 1)K^{1/n} + \frac{K}{K^{(1 - 1/n)}} - n \\
&=& nK^{1/n} - K^{1/n} + K^{1/n} - n \\
&=& n(K^{1/n} - 1)
\end{eqnarray}

すなわち，下式になります．

$$U_{lub} = U_s + n (K^{1/n} - 1) \tag{13.1}$$

ここで，\(U_s\)は下式になります．

$$U_s = \frac{C_s}{T_s} = \frac{T_1 - T_s}{T_s} = R_s - 1$$

\(R_s\)は以下になります．

$$R_s = (U_s + 1)$$

\(K\)は以下のように書き換えられます．

$$K = \frac{2}{R_s} = \frac{2}{U_s + 1}$$

最終的に下式が導出されます．

$$U_{lub} = U_s + n \left[ \left( \frac{2}{U_s + 1} \right)^{1/n} - 1 \right]$$

式\((13.1)\)の極限（\(n \to \infty\)）をとると，\(U_s\)の関数としてのスケジュール可能上限は下式になります．

$$\lim_{n \to \infty} U_{lub} = U_s + \ln{(K)} = U_s + \ln{\left( \frac{2}{U_s + 1} \right)} \tag{13.2}$$

\(n\)個の周期タスクセットとPSのCPU利用率がそれぞれ\(U_p\)と\(U_s\)の場合，RMスケジューリングにおける周期タスクのスケジュール可能性解析は以下を満たす場合に保証されます．

$$U_p + U_s \leq U_s + n \left( K^{1/n} - 1 \right)$$

すなわち，下式になります．

$$U_p \leq n \left[ \left( \frac{2}{U_s + 1} \right)^{1/n} - 1 \right] \tag{13.3}$$

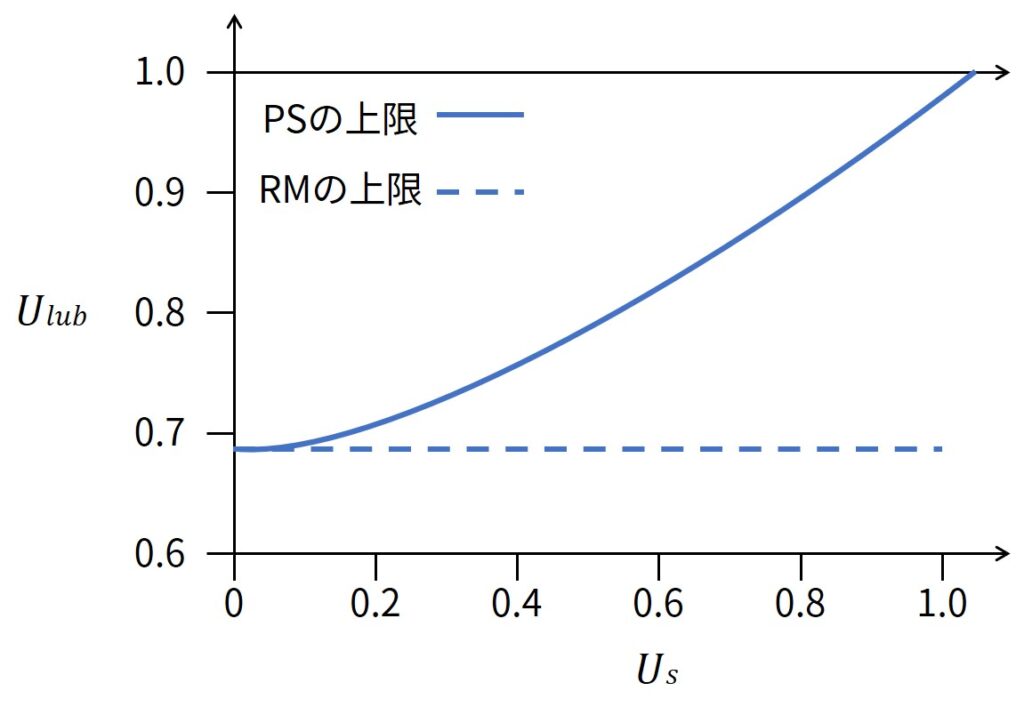
上図に式\((13.2)\)における\(U_s\)の関数を示します．

比較のために，RMのスケジュール可能上限も入れてあります．

式\((13.3)\)のスケジュール可能性判定テストは，周期タスクのように振る舞う全ての非周期サーバにも有効なことに注意して下さい．

Hyperbolic Boundを利用する場合，PSにおけるタスクセットのスケジュール可能性判定テストは，下式になります．

$$ \prod_{i=1}^n (U_i + 1) \leq \frac{2}{U_s + 1} \tag{13.4}$$

最終的には，PSが最高優先度における周期タスク\(\tau_i\)の応答時間\(R_i\)は以下の漸化式になります．

$$R_i = C_i + \left\lceil \frac{R_i}{T_s} \right\rceil C_s + \sum_{j=1}^{i-1} \left\lceil \frac{R_i}{T_j} \right\rceil C_j$$

PSにおける最大CPU利用率

周期タスクセットにおいて，スケジュール可能な非周期サーバのパラメータ（\(C_s\)と\(T_s\)）はどのように算出するのでしょうか？

最初に，タスクセットのスケジュール可能性を保証できる非周期サーバのCPU利用率\(U_s^{max}\)を算出します．

応答時間は天井関数（Ceiling Function）があるので，扱いが難しいです．

なので，式\((13.3)\)より厳密な式\((13.4)\)のHyperbolic Boundから\(U_s^{max}\)を算出します．

まず，\(P\)を以下に定義します．

$$ P \stackrel{\mathrm{def}}{=} \prod_{i=1}^n (U_i + 1) \tag{13.5}$$

タスクセットのスケジュール可能性において，式\((13.4)\)により，以下が成立しなければなりません．

$$P \leq \frac{2}{U_s + 1} $$

すなわち，下式が成立します．

$$U_s \leq \frac{2 - P}{P}$$

したがって，\(U_s^{max}\)は下式になります．

$$U_s^{max} = \frac{2 - P}{P}$$

\(U_s\)は\(U_s^{max}\)以下でなければなりません．

\(U_s\)において，同じCPU利用率で無限の\((C_s, T_s)\)の組合せがあります．

なので，非周期タスクの応答性を向上する\((C_s, T_s)\)の組合せをどのように選んだら良いのでしょうか？

簡単な方法は，非周期サーバに最高優先度を割り当てることです．

つまり，RMスケジューリングでは最短周期を割り当てます．

しかし，短い周期\(T_s\)は小さい容量\(C_s\)になり，結果として非周期タスクの実行において高いフラグメンテーション（高いオーバヘッド）を引き起こしますので，\(T_s < T_1\)の場合はあまり役に立ちません．

したがって，周期タスクや非周期サーバ間の優先度のタイブレーク方式は，非周期サーバを優先します．

なので，非周期サーバの最高優先度は\(T_s=T_1\)で実現でき，その容量は\(C_s = U_s T_s\)になります．

PSにおける非周期タスクのスケジュール可能性解析

絶対デッドラインによるファーム非周期タスクのオンライン（実行時）でのリアルタイム性を保証するためには，PSにより扱われる非周期タスクのジョブの応答時間を見積もる必要があります．

このためには，1つの非周期ジョブ\(J_a\)が時刻\(r_a\)に到着し，最悪実行時間\(C_a\)，絶対デッドライン\(D_a\)の場合を考慮します．

最悪の場合において，非周期ジョブは多くとも実行前に非周期サーバの1周期待つ可能性があります．

もし\(C_a \leq C_s\)ならば，非周期ジョブは非周期サーバの2周期以内に必ず終了します．

すなわち，下式が成立する場合にリアルタイム性を保証できます．

$$2T_s \leq D_a$$

任意の最悪実行時間において，非周期ジョブは非周期サーバの\( \left \lceil C_a / C_s \right \rceil \)周期以内に必ず終了します．

すなわち，下式が成立する場合にリアルタイム性を保証できます．

$$T_s + \left\lceil \frac{C_a}{C_s} \right\rceil T_s \leq D_a$$

非周期サーバが周期内に実行が終了する場合を考慮していないので，このスケジュール可能性判定テストは十分条件です．

必要十分条件のスケジュール可能性判定テストは，周期タスクの中でPSが最高優先度（最短周期）の場合に導出できます．

この場合，非周期サーバは周期の最初にいつも実行します．

非周期タスクの終了時刻は，正確に見積もることができます．

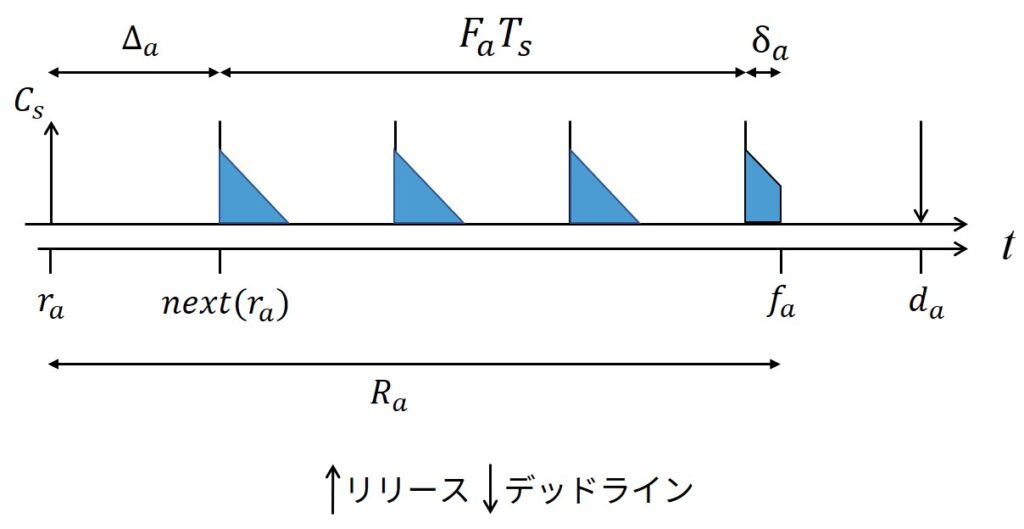
上図に示すように，下式を定義します．

\begin{eqnarray}
F_a &\stackrel{\mathrm{def}}{=}& \left\lceil \frac{C_a}{C_s} \right\rceil - 1 \\
next(r_a) &\stackrel{\mathrm{def}}{=}& \left\lceil \frac{r_a}{T_s} \right\rceil T_s
\end{eqnarray}

非周期ジョブ\(J_a\)の初期遅延は，\(\Delta_a = next(r_a) - r_a\)になります．

\(F_a C_s\)は非周期サーバの周期\(F_a\)内に\(J_a\)により消費される合計時間です．

なので，次の非周期サーバの周期で消費できる残り実行時間は下式になります．

$$\delta_a = C_a - F_a C_s$$

結果として，応答時間\(R_a\)は下式に算出できます．

$$R_a = \Delta_a + F_a T_s + \delta_a$$

また，応答時間\(R_a\)は下式のように書き換えられます．

$$R_a = \Delta_a + C_a + F_a (T_s - C_s) \tag{13.6}$$

式\((13.6)\)の期間\(F_a (T_s - C_s)\)は実行しない非周期サーバの間隔\(F_a\)と各々のサイズ\((T_s - C_s)\)の積による遅延となります．

そして，非周期ジョブのスケジュール可能性判定テストは，下式が成立する場合においてのみリアルタイム性を保証することができます．

$$R_a \leq D_a$$

まとめ

今回は，非周期サーバPolling Server（PS）を紹介しました．

具体的には，以下の内容を解説しました．

• PSの特徴
• PSのスケジュール可能性解析
• PSにおける最大CPU利用率
• PSにおける非周期タスクのスケジュール可能性解析

非周期サーバPSの重要なポイントは，周期タスクのように振る舞うことで，周期タスクのスケジュール可能性解析や応答時間解析を応用できることです．

今回の記事を読んで頂いた方は，LiuとLaylandのモデルの理解も深まったと思います．

リアルタイムシステムで使われているリアルタイムOSは，主にC言語で書かれています．

私にC言語の無料相談をしたいあなたは，公式LINE「ChishiroのC言語」の友だち追加をお願い致します．

私のキャパシティもあり，一定数に達したら終了しますので，今すぐ追加しましょう！

独学が難しいあなたは，元東大教員がおすすめするC言語を学べるオンラインプログラミングスクール5社で自分に合うスクールを見つけましょう．後悔はさせません！

次回はこちらからどうぞ．