【第9回】元東大教員から学ぶリアルタイムシステム「Deadline Monotonicスケジューリング」

こういった私から学べます．

前回を読んでいない方はこちらからどうぞ．

リアルタイムシステムの記事一覧はこちらからどうぞ．

リアルタイムシステムで使われているリアルタイムOSは，主にC言語で書かれています．

私にC言語の無料相談をしたいあなたは，公式LINE「ChishiroのC言語」の友だち追加をお願い致します．

私のキャパシティもあり，一定数に達したら終了しますので，今すぐ追加しましょう！

独学が難しいあなたは，元東大教員がおすすめするC言語を学べるオンラインプログラミングスクール5社で自分に合うスクールを見つけましょう．後悔はさせません！

Deadline Monotonic（DM）スケジューリング

Deadline Monotonic（DM）スケジューリングは，絶対デッドラインの早いタスクに高い優先度を割り当てる固定優先度スケジューリングです．

RMやEDFは，第5回リアルタイムシステムで紹介した想定A1，A2，A3，A4に依存したスケジューリングです．

※想定A1，A2，A3，A4は以下になります．

A1：周期タスク\(\tau_i\)のジョブは一定の周期で起動する．2つの連続した起動の間の間隔\(T_i\)はタスクの周期である．

A2：全ての周期タスク\(\tau_i\)のジョブは同じ最悪実行時間\(C_i\)を持つ．

A3：全ての周期タスク\(\tau_i\)のジョブは同じ相対デッドライン\(D_i\)を持ち，周期\(T_i\)と同じである．

A4：タスクセット\(\Gamma\)にある全ての周期タスクは独立している．すなわち，タスク間の依存関係やリソース制約がない．

https://hiroyukichishiro.com/real-time-systems-vol5/

具体的には，想定A3は想定デッドラインと周期が同じであることを課します．

リアルタイムアプリケーションでは，この条件が必ずしも正しいとは限りません．

想定A3を緩めることで，より柔軟なモデルを提供することができます．

例えば，ジッタや起動の制約で，周期より応答時間を短くすることを要求するタスクを扱うことができます．

DMの優先度割り当ては，固定優先度スケジューリングにおいて「周期と相対デッドラインが同じ」という制約を緩めます．

1982年にLeungとWhiteheadがRMの拡張として相対デッドラインが周期より短い（Constrained Deadline）DMを提案しました．

特に，各々の周期タスク\(\tau_i\)は以下の4つのパラメータから構成されています．

• \(\Phi_i\)：位相
• \(C_i\)：最悪実行時間
• \(D_i\)：相対デッドライン
• \(T_i\)：周期

これらのパラメータは，以下の関係にあります．

\begin{cases}
C_i \leq D_i \leq T_i \\
r_{i,k} = \Phi_i + (k - 1) T_i \\
d_{i,k} = r_{i,k} + D_i
\end{cases}

上式を図で表すと，下図になります．

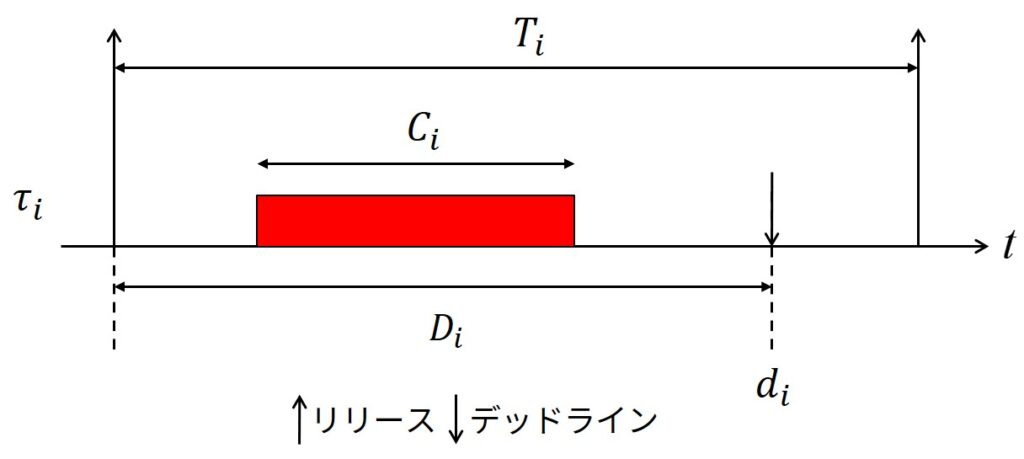
DMによると，各々のタスク\(\tau_i\)は相対デッドライン\(D_i\)の短い順に高い優先度\(P_i\)を割り当てます．

相対デッドラインは一定なので，DMは固定優先度スケジューリングです．

RMと同様に，DMはプリエンプティブ（横取り可能）なので，現在実行しているタスクは新しく到着した短い相対デッドライン（高い優先度）のタスクにプリエンプション（横取り）されます．

DMスケジューリングは最適です．

すなわち，あらゆる固定優先度スケジューリングでスケジュール可能なタスクセットは，DMでスケジュール可能です．

DMのスケジュール可能性解析

相対デッドラインが周期より短いタスクセットのスケジュール可能性は，タスクの周期を相対デッドラインに変換した下記のCPU利用率をベースにしたテストで保証することができます．

$$\sum_{i=1}^n \frac{C_i}{D_i} \leq n (2^{1/n} - 1)$$

しかし，このスケジュール可能性判定テストは，CPUのワークロード（処理の負荷）を過大評価しているので，とても悲観的です．

悲観的なスケジュール可能性判定テストを厳密にするためには，以下の点に注目します．

• 最悪のCPU時間の要求は，全てのタスクが同時にリリースした時に発生します．つまり，クリティカルインスタントの時です．
• 各々のタスク\(\tau_i\)において，最悪実行時間の合計と高優先度タスクの干渉（プリエンプション）は，相対デッドライン\(D_i\)以下でなければなりません．

タスクは相対デッドラインの短い順になることを想定しています．つまり，下式の関係になります．

$$ i < j \Leftrightarrow D_i < D_j$$

DMのスケジュール可能性判定テストは，下式になります．

$$\forall i : 1 \leq i \leq n \ \ C_i + I_i \leq D_i$$

ここで，\(I_i\)はタスク\(\tau_i\)の干渉時間です．

干渉時間\(I_i\)は相対デッドライン\(D_i\)以前の全ての高優先度タスクの最悪実行時間の合計になります．

$$ I_i = \sum_{j=1}^{i-1} \left\lceil \frac{D_i}{T_j} \right\rceil C_j$$

このスケジュール可能性判定テストは十分条件で，タスクセットのスケジュール可能性を保証する必要条件ではありません．

タスク\(\tau_i\)の干渉時間\(I_i\)は，タスク\(\tau_i\)が各々の高優先度タスク\(\tau_j\)により\(\lceil D_i/T_j \rceil\)回干渉されることを想定して算出するからです．

しかし，下図のように，実際のタスク\(\tau_i\)の干渉時間は，早く終了することがあるので，\(I_i\)より短くなることがあります．

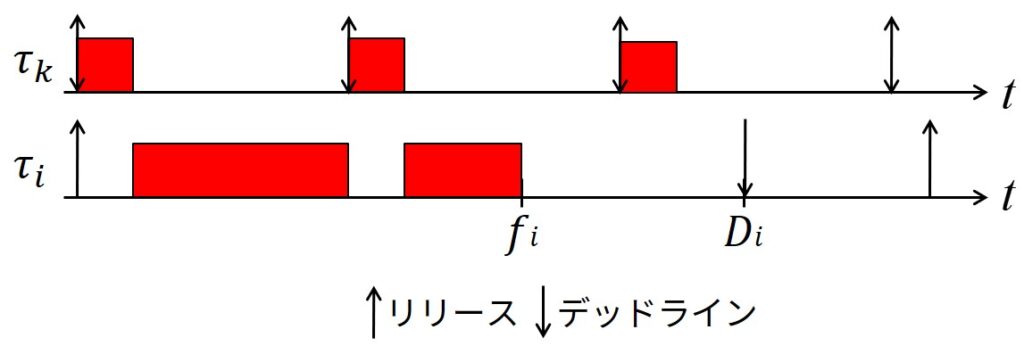
DM向けスケジュール可能性判定テストの必要十分条件を見つけるためには，高優先度タスクの正確な干渉時間をタスク毎に算出しなければなりません．

一般的に，この方法はタスク\(\tau_i\)は相対デッドライン\(D_i\)までのスケジュールの構築が必要なので，非常に計算コストが高いです．

Audsleyらは周期タスクの正確な干渉時間を算出する効果的な方法を提案し，DMのスケジュール可能性判定テストの必要十分条件になる応答時間解析（RTA：Response Time Analysis）を導きました．

応答時間解析（RTA：Response Time Analysis）

Audsleyらにより提案された応答時間解析によると，周期タスク\(\tau_i\)の最長応答時間\(R_i\)は，クリティカルインスタント（タスクの応答時間が最大値になる時刻）の時に算出できます．

高優先度タスクによるタスク\(\tau_i\)の干渉時間\(I_i\)の合計は下式になります．

$$R_i = C_i + I_i$$

ここで，\(I_i\)は下式になります．

$$I_i = \sum_{j=1}^{i-1} \left\lceil \frac{R_i}{T_j} \right\rceil C_j$$

したがって，\(R_i\)は下式になります．

$$R_i = C_i + \sum_{j=1}^{i-1} \left\lceil \frac{R_i}{T_j} \right\rceil C_j \tag{9.1}$$

\(R_i\)は式\((9.1)\)の両辺にあるので，シンプルな解法はありません．

タスク\(\tau_i\)の最悪応答時間は式\((9.1)\)を満たす\(R_i\)の最小値になります．

しかし，間隔\([0, D_i)\)のサブセットのみがスケジュール可能性判定テストに必要なことに注意して下さい．

実際，タスク\(\tau_i\)の干渉時間は高優先度タスクのリリースした時のみ増えます．

表記を簡略化するために，\(R_i^{(k)}\)を\(R_i\)の\(k\)番目の推定，\(I_i^{(k)}\)を間隔\([0, R_i^{(k)})\)におけるタスク\(\tau_i\)の干渉時間と置くと，下式になります．

$$I_i^{(k)} = \sum_{j=1}^{i-1} \left\lceil \frac{R_i^{(k)}}{T_j} \right\rceil C_j$$

\(R_i\)の算出は以下の3つの手順になります．

応答時間\(R_i\)の算出方法

応答時間\(R_i\)の算出方法を紹介します．

step
1

反復は，\(R_i^{(0)} = \sum_{j=1}^i C_j\)から開始します．これはタスク\(\tau_i\)が終了可能な最初の時点です．

step
2

間隔\([0, R_i^{(k)})\)における実際の干渉\(I_i^k\)は，式\((9.1)\)により算出されます．

step
3

もし\(I_i^{(k)} + C_i = R_i^{(k)}\)ならば，\(R_i^{(k)}\)はタスク\(\tau_i\)の最悪応答時間になります．

すなわち，\(R_i = R_i^{(k)}\)になります．そうでなければ次の推定は以下になります．

$$R_i^{(k+1)} = I_i^{(k)} + C_i$$

この反復はステップ2から継続します．

\(R_i\)が算出された場合，タスク\(\tau_i\)のスケジュール可能性は\(R_i \leq D_i\)の場合のみ保証されます．

DMのスケジュール例

スケジュール可能性判定テストを明らかにするためには，下表の周期タスクセットを考慮しましょう．

このタスクセットは時刻\(t=0\)で同時に全てのタスクが起動します．

\(\tau_i\)：タスク	\(C_i\)：最悪実行時間	\(T_i\)：周期	\(D_i\)：相対デッドライン
\(\tau_1\)	1	4	3
\(\tau_2\)	1	5	4
\(\tau_3\)	2	6	5
\(\tau_4\)	1	11	10

タスク\(\tau_4\)のスケジュール可能性を保証するためには，\(R_4\)を算出し，\(R_4 \leq D_4\)であることを保証しなければなりません．

DMにより生成されるスケジュール例と算出のステップを下図に示します．

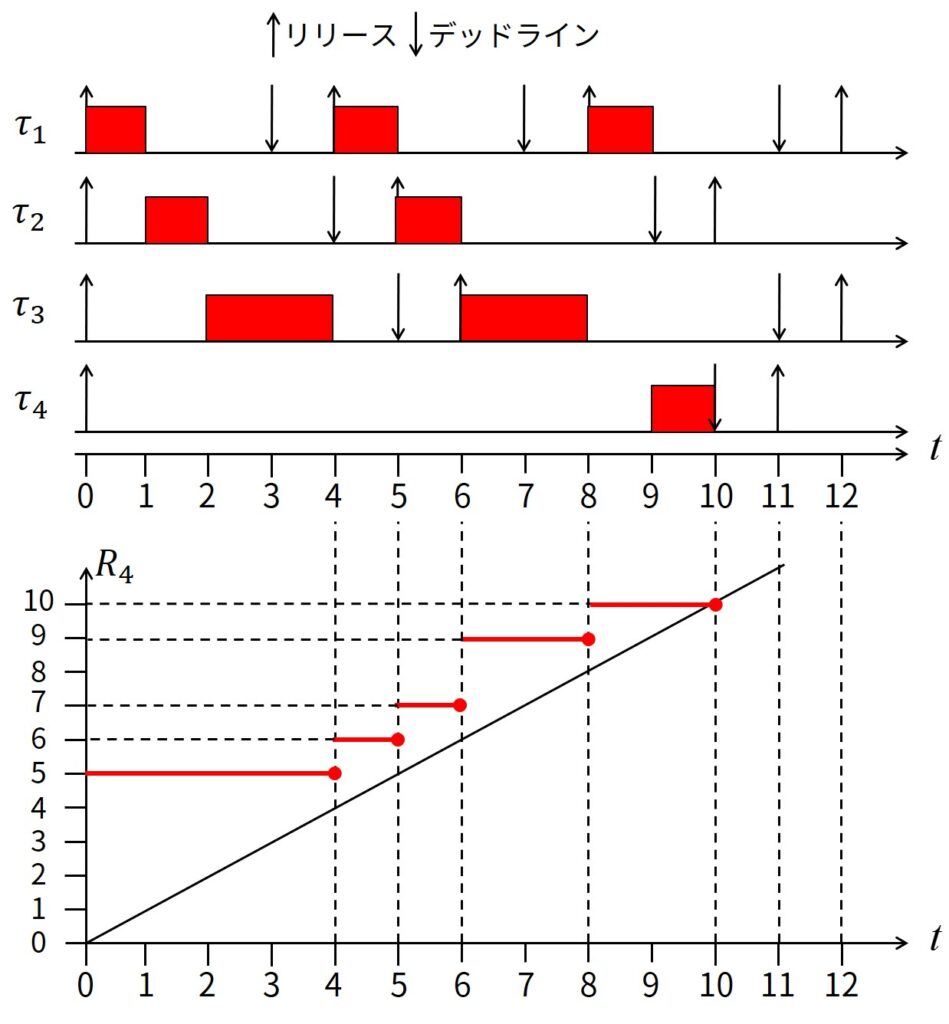
step
0

$$R_4^{(0)} = \sum_{i=1}^4 C_i = 5$$

\(I_4^{(0)} = 5\)かつ\(I_4^{(0)} + C_4 > R_4^{(0)}\)なので，\(\tau_4\)は\(R_4^{(0)}\)で終了しません．

step
1

$$R_4^{(1)} = I_4^{(0)} + C_4 = 6$$

\(I_4^{(1)} = 6\)かつ\(I_4^{(1)} + C_4 > R_4^{(1)}\)なので，\(\tau_4\)は\(R_4^{(1)}\)で終了しません．

step
2

$$R_4^{(2)} = I_4^{(1)} + C_4 = 7$$

\(I_4^{(2)} = 8\)かつ\(I_4^{(2)} + C_4 > R_4^{(2)}\)なので，\(\tau_4\)は\(R_4^{(2)}\)で終了しません．

step
3

$$R_4^{(3)} = I_4^{(2)} + C_4 = 9$$

\(I_4^{(3)} = 9\)かつ\(I_4^{(3)} + C_4 > R_4^{(3)}\)なので，\(\tau_4\)は\(R_4^{(3)}\)で終了しません．

step
4

$$R_4^{(4)} = I_4^{(3)} + C_4 = 10$$

\(I_4^{(4)} = 9\)かつ\(I_4^{(4)} + C_4 = R_4^{(4)}\)なので，\(\tau_4\)は\(R_4 = R_4^{(4)} = 10\)で終了します．

\(R_4 \leq D_4\)なので，\(\tau_4\)はデッドラインまでにスケジュール可能です．

もし\(R_i \leq D_i\)が全てのタスクで成立する場合，タスクセットはDMでスケジュール可能です．

C言語によるスケジュール可能性テストのコードは以下になります．

qsort関数の使い方を知りたいあなたはこちらからどうぞ．

上記のアルゴリズムは，準多項式の計算量になります．

実際，全体のタスクセットは保証には計算量\(\mathcal{O}(nN)\)のステップが必要です．

ここで，\(n\)はタスク数，\(N\)は71～73行目のループの回数を表します．

\(N\)は\(n\)に直接は依存しませんが，周期の関係に依存します．

実行結果は以下になります．

DMのスケジュール例のタスクセットを入力したところ，正しくスケジュール可能性を判定できていることがわかります（Feasibleと表示）．

ワークロード解析

他の固定優先度スケジューリングのスケジュール可能性判定テストの必要十分条件はLehoczkyらにより提案されました．

このテストは，下記のLevel-iワークロードのコンセプトに基づいています．

定義9.1：Level-iワークロード\(W_i (t)\)は，タスク\(\tau_i\)とタスク\(\tau_i\)より高優先度の全てのタスク\(\tau_h (優先度：P_h > P_i)\)が間隔\([0, t)\)に必要な累積した最悪実行時間である．

周期タスクのセットにおいて，Level-iワークロードは下式で算出できます．

$$W_i(t) = C_i + \sum_{h: P_h > P_i} \left\lceil \frac{t}{T_h} \right\rceil C_h \tag{9.2}$$

このテストは，以下の定理で証明されています．

定理9.1：完全にプリエンプティブ可能な周期タスクセットは，以下の条件を満たす場合においてのみスケジュール可能である（証明は省略）．

$$\forall i = 1, ..., n\ \ \ \exists t \in [0, D_i): W_i(t) \leq t \tag{9.3}$$

BiniとButtazzoは，以下のTesting Set（\(\cal TS_i\)）に対して，式\(（9.3）\)がチェックしなければならない条件を制限する手法を「Schedulability Analysis of Periodic Fixed Priority Systems」で提案しました．

$$ \cal TS_i \stackrel{\mathrm{def}}{=} P_{i-1} (D_i)$$

\(\cal P_i(t)\)は，以下の繰り返し表現で定義します．

\begin{cases}
P_0 (t) &=& \{t\} \\
P_i (t) &=& P_{i-1} \left( \left\lfloor \frac{t}{T_i} \right\rfloor T_i \right) \cup P_{i-1} (t)
\end{cases}

スケジュール可能性判定テストは，以下の定理で表現されます．

定理9.2：完全にプリエンプティブ可能な周期タスクは以下の条件を満たす場合においてのみ固定優先度スケジューリングでスケジュール可能である（証明は省略）．

$$\forall i = 1, …, n\ \ \ \exists t \in {\cal TS_i}: W_i(t) \leq t \tag{9.4}$$

式\((9.4)\)の利点は，より簡潔な条件のセットで公式化できることです．

また，Hyperplanesテストという効果的な十分条件のテストを導出しました．

このテストは準多項式の計算量が必要ですが，平均処理時間は応答時間解析より短くなります．

さらには，このテストの斬新な機能は，タスクの受け入れ率と計算量を釣り合わせるパラメータを使って調整できることです．

※タスクの受け入れ率とは，多数を追加した新しいタスクセットがスケジュール可能であれば受け入れます．そうでなければ，タスクの受け入れを拒否します．

調整可能な特性は，以下のケースで重要になります．

• 準多項式のテストの処理の負荷が高く，高いCPU利用率を利用できない場合．
• 正確なテストによるオーバヘッドがオンラインのアドミッションコントロール（タスク受け入れテスト）に対してあまりにも高すぎる場合．

まとめ

今回は，Deadline Monotonic（DM）スケジューリングを解説しました．

具体的には，以下の内容を解説しました．

• DMは相対デッドラインの早いタスクに高い優先度を割り当て
• DMは相対デッドラインが周期より短い場合に最適な固定優先度スケジューリング
• DMのスケジュール可能上限\(\sum_{i=1}^n C_i / D_i \leq n (2^{1/n} - 1)\)
• DMのスケジュール可能性解析の必要十分条件は応答時間解析（RMにも適用可能）
• DMのワークロード解析は受け入れ率と計算量を調整可能

DMで登場した応答時間解析は有名な手法なので，是非きちんと理解しましょう！

次回は相対デッドラインが周期より短いEarliest Deadline First（EDF）スケジューリングを説明します．

リアルタイムシステムで使われているリアルタイムOSは，主にC言語で書かれています．

私にC言語の無料相談をしたいあなたは，公式LINE「ChishiroのC言語」の友だち追加をお願い致します．

私のキャパシティもあり，一定数に達したら終了しますので，今すぐ追加しましょう！

独学が難しいあなたは，元東大教員がおすすめするC言語を学べるオンラインプログラミングスクール5社で自分に合うスクールを見つけましょう．後悔はさせません！

次回はこちらからどうぞ．