【第10回】元東大教員から学ぶリアルタイムシステム「相対デッドラインが周期より短いEDFスケジューリング」

こういった私から学べます．

前回を読んでいない方はこちらからどうぞ．

リアルタイムシステムの記事一覧はこちらからどうぞ．

リアルタイムシステムで使われているリアルタイムOSは，主にC言語で書かれています．

私にC言語の無料相談をしたいあなたは，公式LINE「ChishiroのC言語」の友だち追加をお願い致します．

私のキャパシティもあり，一定数に達したら終了しますので，今すぐ追加しましょう！

独学が難しいあなたは，元東大教員がおすすめするC言語を学べるオンラインプログラミングスクール5社で自分に合うスクールを見つけましょう．後悔はさせません！

相対デッドラインが周期より短いEarliest Deadline First（EDF）スケジューリング

Earliest Deadline First（EDF）スケジューリングで相対デッドラインが周期より短い場合は，Processor Demandによりスケジュール可能性を解析することができます．

Processor DemandはBaruahらにより提案されました．

Processor Demand

一般的には，区間\([t_1, t_2)\)におけるタスク\(\tau_i\)のProcessor Demandは処理時間\(g_i(t_1, t_2)\)になります．

処理時間\(g_i(t_1, t_2)\)は，タスク\(\tau_i\)が区間\([t_1, t_2)\)に起動して，この区間内に終了するために必要な長さで，下式になります．

$$g_i(t_1, t_2) = \sum_{r_{i,k} \geq t_1, \ d_{i,k} \leq t_2} C_i$$

全体のタスクセットにおいて，\([t_1, t_2)\)のProcessor Demandは下式になります．

$$g(t_1, t_2) = \sum_{i=1}^n g_i(t_1, t_2)$$

次に，タスクセットのスケジュール可能性は，あらゆる区間においてProcessor DemandがCPUの利用可能な時間を超えない場合においてのみ保証されます．

すなわち，下式を満たす場合においてのみ保証されます．

$$\forall t_1, t_2 \ \ \ g(t_1, t_2) \leq (t_2 - t_1)$$

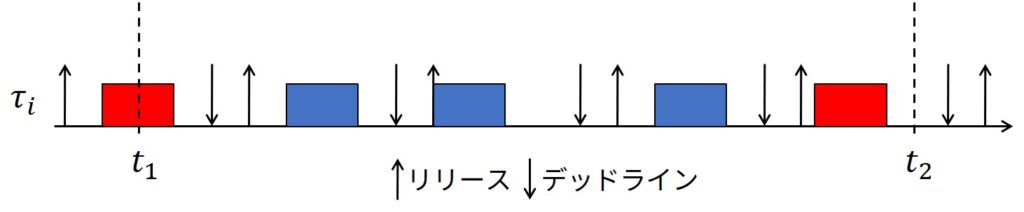
上図によると，区間\([t_1, t_2)\)におけるタスク\(\tau_i\)のジョブ数は下式になります．

$$\eta_i (t_1, t_2) = \max \left\{ 0, \left\lfloor \frac{t_2 + T_i - D_i - \Phi_i}{T_i} \right\rfloor - \left\lceil \frac{t_1 - \Phi_i}{T_i} \right\rceil \right\}$$

区間\([t_1, t_2)\)におけるProcessor Demandは下式になります．

$$g(t_1, t_2) = \sum_{i=1}^n \eta_i (t_1, t_2) C_i$$

もし相対デッドラインが周期より短いか同じで，周期タスクが全て時刻\(t=0\)に同時に起動する場合（全てのタスクの位相\(\Phi_i = 0\)の場合），区間\([0, L)\)におけるProcessor Demandに含まれるジョブ数は下式になります．

$$\eta_i (0, L) = \left\lfloor \frac{L + T_i - D_i}{T_i} \right\rfloor $$

区間\([0, L)\)におけるProcessor Demandは下式になります．

$$g(0, L) = \sum_{i=1}^n \left\lfloor \frac{L + T_i - D_i}{T_i} \right\rfloor C_i $$

関数\(g(0, L)\)はDemand Bound Function（DBF）と呼ばれます．

$${\sf dbf} (t) \stackrel{\mathrm{def}}{=} \sum_{i=1}^n \left\lfloor \frac{t + T_i - D_i}{T_i} \right\rfloor C_i $$

相対デッドラインが周期より短いか同じ場合の周期タスクセットは，以下の条件を満たす場合においてのみEDFでスケジュール可能です．

$$\forall t > 0 \ \ \ {\sf dbf}(t) \leq t \tag{10.1}$$

タスクの相対デッドラインが周期と同じ場合，Processor Demandによるスケジュール可能性判定テストは，スケジュール可能上限の1（100%）になります．

この結果は，JeffayとStoneにより以下の定理で証明されています．

定理10.1：相対デッドラインが周期と同じタスクセットは以下の条件を満たす場合においてのみスケジュール可能である．

$$\forall L > 0 \ \ \ \sum_{i=1}^n \left\lfloor \frac{L}{T_i} \right\rfloor C_i \leq L \tag{10.2}$$

証明：この定理は，LiuとLaylandのスケジュール可能上限と同様であることを示すことで証明できます．

$$U = \sum_{i=1}^n \frac{C_i}{T_i} \leq 1 \tag{10.3}$$

式\((10.3) \Rightarrow (10.2)\)は，\(U \leq 1\)の場合，全ての\(L (L \geq 0)\)において以下を満たすことで証明できました．

$$ L \geq UL = \sum_{i=1}^n \left( \frac{L}{T_i} \right) C_i \geq \sum_{i=1}^n \left\lfloor \frac{L}{T_i} \right\rfloor C_i $$

式\((10.3) \Leftarrow (10.2)\)の証明は，対偶である式\(\lnot (10.3) \Rightarrow \lnot (10.2)\)を示します．

すなわち，\(U > 1\)かつ\(L \geq 0\)で式\((10.2)\)が成立しないことを示します．

\(U > 1\)の場合，\( L = H = \operatorname{lcm}(T_1, ..., T_n)\)により下式になるので，対偶を証明できました．

$$H < HU = \sum_{i=1}^n \left( \frac{H}{T_i} \right) C_i = \sum_{i=1}^n \left\lfloor \frac{H}{T_i} \right\rfloor C_i$$

□

テスト区間の削減によるProcessor Demandの改良

式\((10.1)\)のスケジュール可能性判定テストは，検証しなければならない間隔の数を減らすことで簡略化できます．

まずは，以下の2つを調査します．

1. もしタスクが周期的で時刻\(t=0\)で同時に起動する場合，スケジュールはハイパーピリオド\(H\)毎に繰り返します．
   この場合，式\((10.1)\)は\(L\)の値が\(H\)以下の場合のみ検証する必要があります．
2. \(g(0, L)\)は，\(L\)が大きくなって絶対デッドライン\(d_k\)以上になるが，次の絶対デッドライン\(d_{k+1}\)未満になるステップ関数である．
   すなわち，\(L = d_k\)において\(g(0, L) < L\)が成立する場合，全ての\(L\)において\(d_k \leq L < d_{k+1}\)も成立する．
   結果として，式\((10.1)\)は\(L\)の値が絶対デッドラインと同じであるかどうかのみ検証すれば良いことがわかります．

テストポイントの数は下式により減らすことができます．

$$\left\lfloor \frac{L + T_i - D_i}{T_i} \right\rfloor \leq \left( \frac{L + T_i - D_i}{T_i} \right)$$

また，\(G(0, L)\)を定義します．

$$G(0, L) = \sum_{i=1}^n \frac{L + T_i - D_i}{T_i} C_i = \sum_{i=1}^n \frac{T_i - D_i}{T_i} C_i + \frac{L}{T_i} C_i$$

\(G(0, L)\)により，下式の関係になります．

$$\forall L > 0, \ \ \ g(0, L) \leq G(0, L)$$

ここで\(G(0, L)\)は下式のように表せます．

$$G(0, L) = \sum_{i=1}^n (T_i - D_i) U_i + LU$$

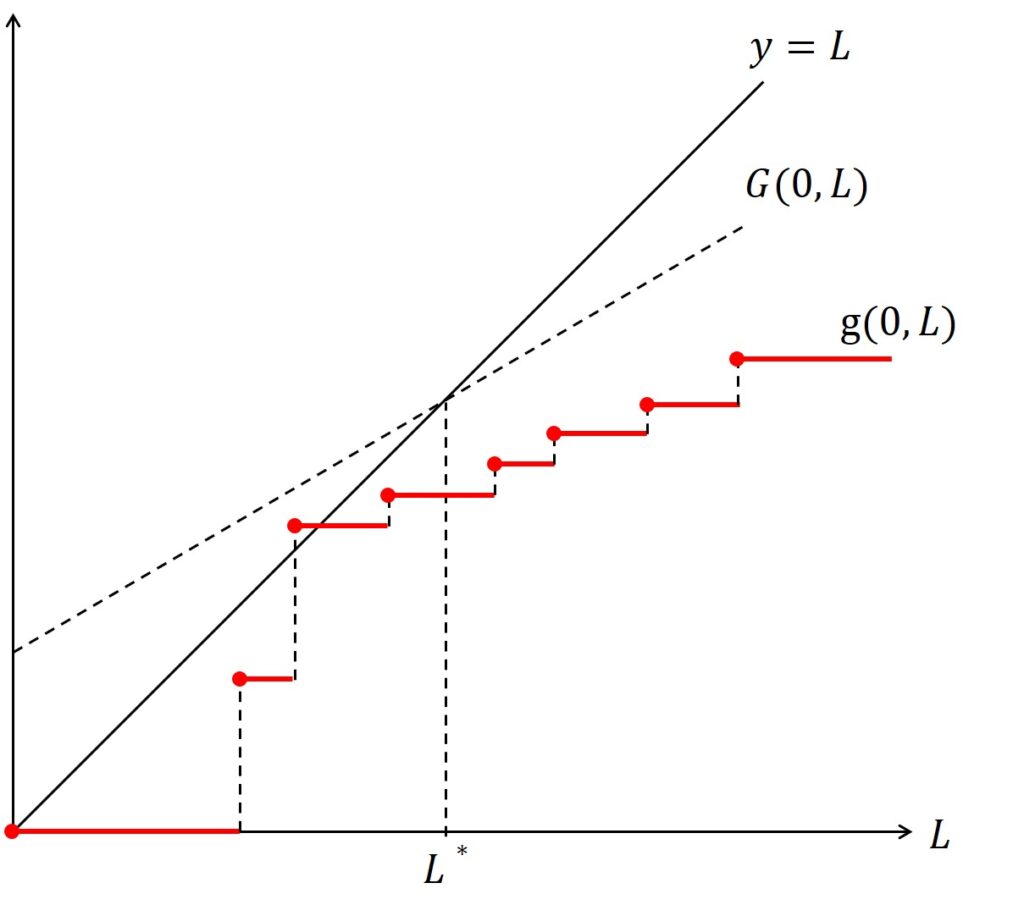
上図によると，\(G(0, L)\)は勾配\(U\)による直線とする\(L\)の関数になります．

もし\(U < 1\)の場合，どの\(G(0, L) = L\)においても\(L=L^*\)となる値が存在します．

明らかに，全ての\(L \geq L^*\)において，\(g(0, L) \leq G(0, L) \leq L\)になりますので，スケジュール可能性が保証できます．

結果として，\(L \geq L^*\)において，式\((10.1)\)を検証する必要はありません．

\(L^*\)の値は\(G(0, L^*)\)になる時刻です．すなわち，下式が成立する場合です．

$$\sum_{i=1}^n (T_i - D_i) U_i + L^* U = L^*$$

上式は下式に変形できます．

$$L^* = \frac{\sum_{i=1}^n (T_i - D_i) U_i}{1 - U} $$

タスクセットは少なくとも最大相対デッドライン\(D_{max}\)までにテストしなければならないことを考慮すると，式\((10.1)\)は以下の定理に組み合わせることができます．

定理10.2：相対デッドラインが周期より短いか同じ周期タスクセットは\(U < 1\)かつ以下の条件を満たした場合においてのみEDFでスケジュール可能になる．

$$\forall t \in {\cal D} \ \ \ {\sf dbf}(t) \leq t \tag{10.4}$$

ここで，\(\cal D\)は下式になります．

$${\cal D} = \{ d_k : d_k \leq \min[H, \max(D_{max}, L^*)] \}$$

\(L^*\)は下式になります．

$$L^* = \frac{\sum_{i=1}^n (T_i - D_i) U_i}{1 - U} $$

\(\tau_i\)：タスク	\(C_i\)：最悪実行時間	\(D_i\)：相対デッドライン	\(T_i\)：周期
\(\tau_1\)	2	4	6
\(\tau_2\)	2	5	8
\(\tau_3\)	3	7	9

上表のタスクセットを使ってProcessor Demandを説明します．

これらの相対デッドラインが周期より短い3つの周期タスクはEDFでスケジュールできることが保証されています．

パラメータ\(U\)，\(L^*\)，\(H\)は下式で算出できます．

$$U = \frac{2}{6} + \frac{2}{8} + \frac{3}{9} = \frac{11}{12} $$

$$L^* = \frac{\sum_{i=1}^n (T_i - D_i) U_i}{1 - U} = 25$$

$$H = \operatorname{lcm}(6, 8, 9) = 72$$

式\((10.4)\)は25未満のあらゆるデッドラインでテストしなければなりません．

チェックポイントのセットは\({\cal D} = \{ 4, 5, 7, 10, 13, 16, 21, 22\}\)になります．

下表にテストの結果を示します．

\(L\)	\(g(0, L)\)	テストの結果
4	2	OK
5	4	OK
7	7	OK
10	9	OK
13	11	OK
16	16	OK
21	18	OK
22	20	OK

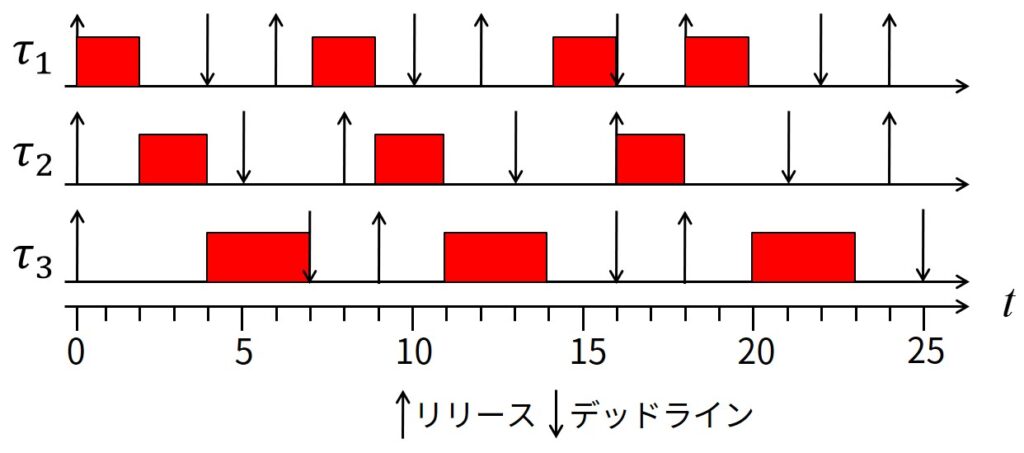
下図に上記のタスクセットをEDFでスケジュールする例を示します．

まとめ

今回は，相対デッドラインが周期より短いEarliest Deadline First（EDF）スケジューリングを解説しました．

具体的には，以下の内容を解説しました．

• Processor Demand
• テスト区間の削減によるProcessor Demandの改良

次回はRMとEDFの比較を説明します．

リアルタイムシステムで使われているリアルタイムOSは，主にC言語で書かれています．

私にC言語の無料相談をしたいあなたは，公式LINE「ChishiroのC言語」の友だち追加をお願い致します．

私のキャパシティもあり，一定数に達したら終了しますので，今すぐ追加しましょう！

独学が難しいあなたは，元東大教員がおすすめするC言語を学べるオンラインプログラミングスクール5社で自分に合うスクールを見つけましょう．後悔はさせません！

次回はこちらからどうぞ．