【日本語訳】NeurIPS（旧NIPS）の論文「Generative Adversarial Networks」【GANs，敵対的生成ネットワーク】【イアン・グッドフェロー】

こういった悩みにお答えします．

こういった私から学べます．

AIのプログラミング言語「C++/Python言語」を学べるおすすめのWebサイトを知りたいあなたはこちらからどうぞ．

独学が難しいあなたは，AIを学べるオンラインプログラミングスクール3社で自分に合うスクールを見つけましょう．後悔はさせません！

国内・海外のAIエンジニアのおすすめ求人サイトを知りたいあなたはこちらからどうぞ．

国内・海外のプロンプトエンジニアのおすすめ求人サイトを知りたいあなたはこちらからどうぞ．

NeurIPS（旧NIPS）の論文「Generative Adversarial Networks」の日本語訳を紹介します．

イアン・グッドフェローによる敵対的生成ネットワーク（GANs：Generative Adversarial Networks）がわかります．

引用数64,000以上のスター論文です！

※図表を含む論文の著作権はGenerative Adversarial Networksの著者に帰属します．

Generative Adversarial Networksの目次は以下になります．

• Abstract
• 1章：Introduction
• 2章：Related work
• 3章：Adversarial nets
• 4章：Theoretical Results
• 5章：Experiments
• 6章：Advantages and disadvantages
• 7章：Conclusions and future work
• Acknowledgments
• References

Generative Adversarial Networksを解説しつつ，私の考えも語ります．

Generative Adversarial Networksの概要と私の日本語訳は以下になります．

We propose a new framework for estimating generative models via adversarial nets, in which we simultaneously train two models:
我々は，2つのモデルを同時に訓練する敵対的ネットワークを介して生成モデルを推定する新しいフレームワークを提案する．

a generative model G that captures the data distribution, and a discriminative model D that estimates the probability that a sample came from the training data rather than G.
すなわち，データ分布を捉える生成モデルGと，サンプルがGではなく訓練データから得られたものである確率を推定する識別モデルDである．

The training procedure for G is to maximize the probability of D making a mistake.
Gの訓練手順は，Dが誤りを犯す確率を最大化することである．

This framework corresponds to a minimax two-player game.
このフレームワークはミニマックス2人ゲームに相当する．

In the space of arbitrary functions G and D, a unique solution exists, with G recovering the training data distribution and D equal to 1/2 everywhere.
任意の関数GとDの空間において，ユニークな解が存在し，Gは訓練データ分布を回復し，Dはどこでも1/2に等しい．

In the case where G and D are defined by multilayer perceptrons, the entire system can be trained with backpropagation.
GとDが多層パーセプトロンで定義される場合，システム全体をバックプロパゲーションで訓練することができる．

There is no need for any Markov chains or unrolled approximate inference networks during either training or generation of samples.
訓練中もサンプル生成中も，マルコフ連鎖や展開されない近似推論ネットワークは必要ない．

Experiments demonstrate the potential of the framework through qualitative and quantitatively evaluation of the generated samples.
生成されたサンプルの定性的・定量的評価を通じて，このフレームワークの可能性を実験により実証する．

https://papers.nips.cc/paper_files/paper/2014/hash/5ca3e9b122f61f8f06494c97b1afccf3-Abstract.html

私の日本語訳の注意点は以下になります．

• 概要は英語と日本語を両方掲載しましたが，本文は私の日本語訳のみを掲載していること（英語で読みたいあなたは原文を読みましょう！）
• 基本的には原文の直訳ですが，わかりにくい箇所は意訳や説明を追加している箇所があること
• 原文の「Acknowledgements」（謝辞）は省略していること
• 本文中に登場する表記「[2]」などは参考文献ですので，興味がある方は本記事の参考文献を参照されたいこと

それでは，Generative Adversarial Networksの本文を読みすすめましょう！

1章：Introduction（はじめに）

深層学習は，自然画像，音声を含むオーディオ波形，自然言語コーパスの記号など，人工知能アプリケーションで遭遇する種類のデータ上の確率分布を表現する，豊かで階層的なモデル[2]を発見することが期待されている．

これまでのところ，ディープラーニングにおける最も顕著な成功は，識別モデル，通常は高次元の豊富な感覚入力をクラスラベルにマッピングするモデルに関わっている[14, 20]．

これらの顕著な成功は，主にバックプロパゲーションとドロップアウトアルゴリズムに基づくものであり，特に勾配が良好な区分的線形ユニット[17, 8, 9]を使用している．

深層生成モデルは，最尤推定や関連戦略で発生する多くの難解な確率的計算を近似することが困難であることや，生成コンテキストで区分的線形ユニットの利点を活用することが困難であることから，あまり大きな影響を及ぼしていない．

我々は，これらの困難を回避する新しい生成モデル推定手順を提案する．

※すべてのコードとハイパーパラメータはhttps://www.github.com/goodfeli/adversarialにある．

提案された敵対的ネットワークのフレームワークでは，生成モデルは敵対者と対戦する．

識別モデルは，サンプルがモデル分布のものかデータ分布のものかを判断することを学習する．

生成モデルは，偽札を作り，それを発見されずに使用しようとする偽造者のチームに似ていると考えることができる．

一方，識別モデルは，偽札を発見しようとする警察に似ている．

このゲームにおける競争は，偽造品が真正品と見分けがつかなくなるまで，両チームを駆り立てて方法を改善させる．

このフレームワークにより，多くの種類のモデルや最適化アルゴリズムに対応した訓練アルゴリズムを得ることができる．

本論文では，生成モデルがランダムなノイズを多層パーセプトロンに通すことでサンプルを生成し，識別モデルも多層パーセプトロンである場合の特別なケースを探索する．

この特別なケースを敵対的ネットワークと呼ぶ．

この場合，非常に成功しているバックプロパゲーションとドロップアウトのアルゴリズム[16]だけを用いて両方のモデルを訓練し，順伝播だけを用いて生成モデルからサンプルを抽出することができる．

近似推論やマルコフ連鎖は必要ない．

2章：Related work（関連研究）

最近まで，深層生成モデルに関するほとんどの研究は，確率分布関数のパラメトリックな仕様を提供するモデルに焦点を当てていた．

このモデルは，対数尤度を最大化することで学習することができる．

このモデルでは，おそらく最も成功しているのはディープ・ボルツマン・マシン（Deep Boltzmann Machine）[25]である．

このようなモデルは一般的に難解な尤度関数を持つため，尤度勾配に対して多くの近似を必要とする．

このような困難さが，尤度を明示的に表現しないが，所望の分布からサンプルを生成することができる「生成機械」を開発する動機となった．

生成確率ネットワーク[4]は，ボルツマンマシンに必要な多数の近似ではなく，厳密なバックプロパゲーションで訓練できる生成マシンの一例である．

本研究では，生成確率ネットワークで使用されるマルコフ連鎖を排除することで，生成マシンの考え方を拡張する．

我々の研究は，次のような観測を利用することで，生成過程を通して微分をバックプロパゲートする．

$$\lim_{\sigma \to 0} \nabla_x \mathbb{E}_{\epsilon \sim N(0, \sigma^2, I)} f(x + \epsilon) = \nabla_x f(x)$$

KingmaとWelling[18]とRezendeら[23]がより一般的な確率的バックプロパゲーション規則を開発し，有限分散を持つガウス分布をバックプロパゲートし，平均だけでなく共分散パラメータまでバックプロパゲートすることを可能にしていたことを，我々はこの研究を開発した時点では知らなかった．

これらのバックプロパゲーションルールにより，この研究でハイパーパラメータとして扱った，生成器の条件付き分散を学習することができる．

KingmaとWelling[18]とRezendeら[23]は，変分オートエンコーダ（VAEs：Variational AutoEncoders）を訓練するために確率的バックプロパゲーションを使用している．

敵対的生成ネットワークと同様に，変分オートエンコーダは，微分可能な生成器ネットワークと第2のニューラルネットワークをペアにしている．

敵対的生成ネットワークとは異なり，VAEにおける第2のネットワークは，近似推論を行う認識モデルである．

GANは可視ユニットを介して微分する必要があるため，離散データをモデル化できないが，VAEは隠れユニットを介して微分する必要があるため，離散潜在変数を持つことができない．

VAE類似のアプローチは他にも存在するが[12, 22]，我々の手法との関連性は低い．

これまでの研究では，判別基準を用いて生成モデルを学習するアプローチも取られてきた[29, 13]．

これらのアプローチでは，深い生成モデルには困難な基準を使用している．

これらの方法は，確率を下界にする変分近似を使用して近似することができない確率の比を含むため，ディープラーニングのモデルで近似することさえ困難である．

ノイズ対比推定（NCE：Noise-Contrastive Estimation）[13]は，固定ノイズ分布からデータを識別するためにモデルを有用にする重みを学習することによって，生成モデルを訓練する．

以前に訓練したモデルをノイズ分布として使用することで，品質が向上する一連のモデルを訓練することができる．

これは，敵対的ネットワークゲームで用いられる形式的な競争と同様の精神を持つ非公式な競争メカニズムとして見ることができる．

NCEの主な限界は，その「識別器」がノイズ分布とモデル分布の確率密度の比によって定義されるため，両方の密度を評価し，バックプロパゲートする能力を必要とすることである．

いくつかの先行研究は，2つのニューラルネットワークを競合させるという一般的な概念を用いている．

最も関連性の高い研究は予測可能性最小化[26]である．

予測可能性最小化では，ニューラルネットワークの各隠れユニットが，他のすべての隠れユニットの値が与えられたときにその隠れユニットの値を予測する第2のネットワークの出力と異なるように訓練される．

この作業は予測可能性最小化とは3つの重要な点で異なる．

1. この作業では，ネットワーク間の競争が唯一の訓練基準であり，ネットワークを訓練するにはそれだけで十分である．予測可能性最小化は，ニューラルネットワークの隠れユニットが他のタスクを達成する間，統計的に独立であることを促す正則化に過ぎない．主要な訓練基準ではない．

2. 競合の性質が異なる．予測可能性最小化では，2つのネットワークの出力が比較され，一方のネットワークは出力を類似させようとし，もう一方は出力を相違させようとする．問題の出力は単一のスカラーである．GANsでは，一方のネットワークが別のネットワークの入力として使用されるリッチで高次元のベクトルを生成し，もう一方のネットワークが処理方法を知らない入力を選択しようとする．

3. 学習プロセスの仕様が異なる．予測可能性の最小化は，最小化すべき目的関数を持つ最適化問題として記述され，学習は目的関数の最小値に近づく．GANsは最適化問題ではなくミニマックスゲームに基づいており，一方のエージェントが最大化，他方のエージェントが最小化を目指す価値関数を持つ．ゲームは，一方のプレイヤーの戦略に関しては最小，他方のプレイヤーの戦略に関しては最大となる鞍点で終了する．

敵対的生成ネットワークは，「敵対的な例」[28]という関連概念と混同されることがある．

敵対的な例とは，データに似ていながら誤分類された例を見つけるために，分類ネットワークへの入力に対して直接勾配ベースの最適化を用いて発見された例のことである．

敵対的な例は生成モデルを訓練するメカニズムではないので，これは今回の研究とは異なる．

その代わりに，敵対的な例は主に，ニューラルネットワークが興味深い振る舞いをすることを示すための分析ツールであり，2つの画像の違いが人間の観察者には知覚できないにもかかわらず，高い信頼性で自信を持って異なる分類をすることがよくある．

このような敵対的な例が存在することは，敵対的生成ネットワークの訓練が非効率的である可能性を示唆している．

なぜなら，このような例は，最新の識別ネットワークに，人間が知覚できるクラスの属性を模倣することなく，自信を持ってクラスを認識させることが可能であることを示しているからである．

3章：Adversarial nets（敵対的ネットワーク）

敵対的モデリングのフレームワークは，モデルが両方とも多層パーセプトロンの場合に適用するのが最も簡単である．

データxに対する生成器の分布\(p_g\)を学習するために，入力ノイズ変数\(p_z(z)\)に対する事前分布を定義し，データ空間へのマッピングを\(G(z; \theta_g)\)として表現する．

ここでGは，パラメータ\(\theta_g\)を持つ多層パーセプトロンで表される微分可能な関数である．

また，1つのスカラーを出力する第2の多層パーセプトロン\(D(x; \theta_d)\)を定義する．

\(D(x)\)はxが\(p_g\)ではなくデータに由来する確率を表す．

Dは訓練例とGからのサンプルの両方に正しいラベルを割り当てる確率を最大化するように訓練する．

同時にGを\(\log(1 - D(G(z)))\)を最小化するように訓練する．

言い換えると，DとGは，価値関数\(V(G, D)\)を持つ以下の2人ミニマックスゲームを行う．

\begin{eqnarray}
\underset{G}{\min} \underset{D}{\max} V(D, G) = \mathbb{E}_{x \sim p_{data}(x)} [\log D(x)] + \mathbb{E}_{z \sim p_z(z)} [ \log(1 - D(G(z)))] \tag{1} \end{eqnarray}

次の章では，敵対的ネットワークの理論的な分析を行い，GとDに十分な容量が与えられたとき，つまりノンパラメトリック極限において，訓練基準によってデータ生成分布を回復できることを示す．

このアプローチの，より形式的でなく，より教育的な説明については，図1を参照されたい．

実際には，反復的な数値的アプローチを使ってゲームを実装しなければならない．

訓練の内部ループでDを完了まで最適化することは計算上不可能であり，有限のデータセットではオーバーフィッティングになる．

その代わりに，Dを最適化するkステップとGを最適化する1ステップを交互に繰り返す．

この結果，Gが十分にゆっくり変化する限り，Dは最適解の近くに維持される．

この手順をアルゴリズム1に正式に示す．

実際には，式1はGがうまく学習するのに十分な勾配を提供しないかもしれない．

学習の初期，Gが貧弱なとき，Dは高い信頼性でサンプルを拒絶することができる．

なぜなら，訓練データとは明らかに異なるからである．

この場合，\(\log (1 - D(G(z)))\)は飽和する．

\(\log (1 - D(G(z)))\)を最小化するようにGを訓練するのではなく，\(\log D(G(z))\)を最大化するようにGを訓練することができる．

この目的関数は，GとDのダイナミクスの固定点は同じになるが，学習の初期にはるかに強い勾配を提供する．

4章：Theoretical Results（理論的結果）

生成器Gは，\(z \sim p_z\)のときに得られるサンプルG(z)の分布として，暗黙的に確率分布\(p_g\)を定義する．

従って，十分な容量と訓練時間が与えられれば，アルゴリズム1が\(p_{data}\)の良い推定量に収束することを望む．

本章の結果はノンパラメトリックな設定で行われる．

例えば，確率密度関数の空間における収束を研究することで，容量が無限のモデルを表現する．

4.1節で，このミニマックスゲームが\(p_g = p_{data}\)に対して大域的最適値を持つことを示す．

そして4.2節で，アルゴリズム1が式1を最適化し，望ましい結果を得ることを示す．

4.1節：Global Optimality of \(p_g = p_{data}\)（\(p_g = p_{data}\)の大域的最適性）

まず，任意の生成器Gに対する最適な識別器Dを考える．

命題1：Gが固定されている場合，最適識別器Dは次のようになる．

$$ D_G^* (x) = \frac{p_{data}(x)}{p_{data}(x) + p_g(x)} \tag{2}$$

証明：識別器Dの訓練基準は，任意の生成器Gが与えられたとき，次の量\(V(G, D)\)を最大化することである．

\begin{eqnarray}
V(G, D) &=& \int_x p_{data}(x) \log (D(x))dx + \int_z p_z (z) \log (1 - D(g(z))) dz \\
&=& \int_x p_{data}(x) \log (D(x)) + p_g(x) \log (1 - D(g(x)) dx
\end{eqnarray}

任意の\((a, b) \in \mathbb{R}^2 \setminus \{0, 0\}\)に対して，関数\(y \rightarrow a \log(y) + b \log(1 - y)\)は [0, 1] において\(\frac{a}{a+b}\)で最大となる．

識別器は，\(Supp(p_{data}) \cup Supp(p_g) \)の外側で定義する必要はないため，証明は終了する．□

Dの訓練目的関数は，条件付き確率\(P(Y = y|x)\)を推定する対数尤度の最大化と解釈できることに注意されたい．

ここで，Yはxが\(p_{data}\)（y=1）か\(p_g\)（y=0）かを示す．

式1のミニマックスゲームは次のように定式化できる．

\begin{eqnarray}
C(G) &=& \underset{D}{\max} V(G, D) \\
&=& \mathbb{E}_{x \sim p_{data}} [\log D_G^* (x)] + \mathbb{E}_{z \sim p_z} [\log (1 - D_G^* (G(z)))] \\
&=& \mathbb{E}_{x \sim p_{data}} [\log D_G^* (x)] + \mathbb{E}_{x \sim p_g} [\log (1 - D_G^* (x))] \\
&=& \mathbb{E}_{x \sim p_{data}} \left[\log \frac{p_{data}(x)}{p_{data}(x) + p_g(x)} \right] + \mathbb{E}_{x \sim p_g} \left[ \log \frac{p_g(x)}{p_{data}(x) + p_g(x)} \right] \tag{3} \\
\end{eqnarray}

定理1：仮想訓練基準C(G)の大域的最小値は，\(p_g = p_{data}\)の場合にのみ達成される．

そのとき，\(C(G) = - \log 4\)になる．

証明：\(p_g = p_{data}\)の場合，\(D_G^* (x) = \frac{1}{2}\)である（式2を考慮）．

従って，\(D_G^* (x) = \frac{1}{2}\)で式3を調べると，\(C(G) = \log \frac{1}{2} + \log \frac{1}{2} = - \log 4\)となる．

これがC(G)の可能な限り最良の値であり，\(p_g = p_{data}\)の場合にのみ到達することを確認するために，以下のことを観察する．

$$ \mathbb{E}_{x \sim p_{data}} [ - \log 2] + \mathbb{E}_{x \sim p_g} [ - \log 2] = - \log 4$$

上式を\(C(G) = V (D_G^*, G)\)からこの式を引くと，下式のようになる．

$$ C(G) = - \log (4) + KL \left( p_{data} \Bigg| \Bigg| \frac{p_{data} + p_g}{2} \right) + KL \left( p_g \Bigg| \Bigg| \frac{p_{data} + p_g}{2} \right) $$

ここでKLはKullback-Leibler divergenceである．

我々はこの式で，モデルの分布とデータ生成過程との間のジェンセン・シャノン発散を認識する．

$$ C(G) = - \log (4) + 2 \cdot JSD (p_{data} || p_g) $$

2つの分布間のジェンセン・シャノン発散は常に非負であり，それらが等しい場合のみゼロになる．

そのため，\(C^* = - \log(4)\)がC(G)の大域的最小値であり，唯一の解は\(p_g = p_{data}\)であることを示した．

すなわち，生成モデルはデータ分布を完全に複製する．□

4.2節：Convergence of Algorithm 1（アルゴリズム1の収束）

命題2：GとDが十分な能力を持ち，アルゴリズム1の各ステップにおいて，識別器がGを与えられたときの最適値に到達することが許され，\(p_g\)は基準を改善するように更新される．

$$ \mathbb{E}_{x \sim p_{data}} [\log D_G^* (x)] + \mathbb{E}_{x \sim p_g} [\log (1 - D_G^* (x))] $$

であれば，\(p_g\)は\(p_{data}\)に収束する．

証明：\(V(G, D)=U(p_g,D)\)を\(p_g\)の関数として考える．

\(U(p_g, D)\)は\(p_g\)に凸であることに注意されたい．

凸関数の上項の微分には，最大になる点での関数の微分が含まれる．

言い換えれば，\(f(x) = \sup_{\alpha \in A} f_\alpha (x)\)であり，\(f_\alpha (x)\)がxにおいてすべての\(\alpha\)に対して凸であるならば，\( \partial f_\beta (x) \in \partial f {\rm\ if} \beta = \arg \sup_{\alpha \in A} f(x)\)となる．

これは，対応するGが与えられた最適なDにおける\(p_g\)の勾配降下更新を計算することと等価である．

\(\sup_D U(p_g, D)\)は，定理1で証明されたように，一意的な大域的最適値を持つ\(p_g\)に凸であるため，\(p_g\)を十分に小さく更新すれば，\(p_g\)は\(p_x\)に収束し，証明は終了する．□

実際には，敵対的ネットワークは関数\(G(z; \theta_g)\)を介して\(p_g\)分布の限られたファミリーを表し，\(p_g\)そのものではなく\(\theta_g\)を最適化するため，証明は適用されない．

しかし，実際には多層パーセプトロンの優れた性能は，理論的な保証がないにもかかわらず，多層パーセプトロンが妥当なモデルであることを示唆している．

5章：Experiments（実験）

我々はMNIST[21]，Toronto Face Database (TFD)[27]，CIFAR-10[19]を含む様々なデータセットで敵対的ネットワークを訓練した．

生成ネットワークは整流器線形活性[17, 8]とシグモイド活性化関数の混合を使用し，識別器ネットはマックスアウト活性化関数[9]を使用した．

識別器ネットワークの訓練にはドロップアウト[16]を適用した．

我々の理論的枠組みでは，生成器の中間層でドロップアウトやその他のノイズを使用することができるが，我々は生成器ネットワークの最下層のみにノイズを入力として使用した．

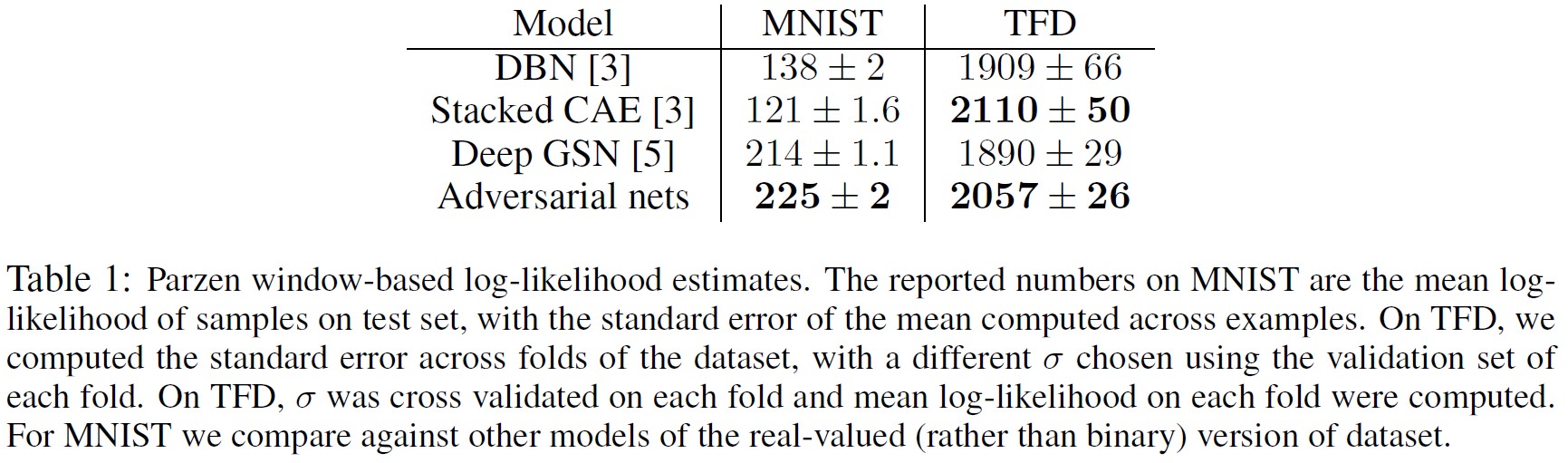
Gで生成されたサンプルにガウシアンパルツェン窓を当てはめ，この分布の下での対数尤度を報告することで，\(p_g\)の下でのテストセットデータの確率を推定する．

ガウシアンのパラメータ\(\sigma\)は，検証集合でのクロスバリデーションによって得られた．

この手順はBreuleuxら[7]で紹介され，厳密尤度が扱いにくい様々な生成モデルに使用されている[24, 3, 4]．

結果は表1に報告されている．

この尤度推定法は分散がやや大きく，高次元空間ではうまくいかないが，我々の知る限りでは最良の方法である．

サンプリングはできるが尤度を直接推定できない生成モデルの進歩は，そのようなモデルをどのように評価するかについてのさらなる研究の動機付けとなる．

図2と図3では，訓練後の生成ネットから引き出されたサンプルを示している．

これらのサンプルが既存の手法で生成されたサンプルよりも優れているという主張はしないが，これらのサンプルは少なくとも文献にある優れた生成モデルと遜色なく，敵対的フレームワークの可能性を強調していると考えている．

6章：Advantages and disadvantages（利点と欠点）

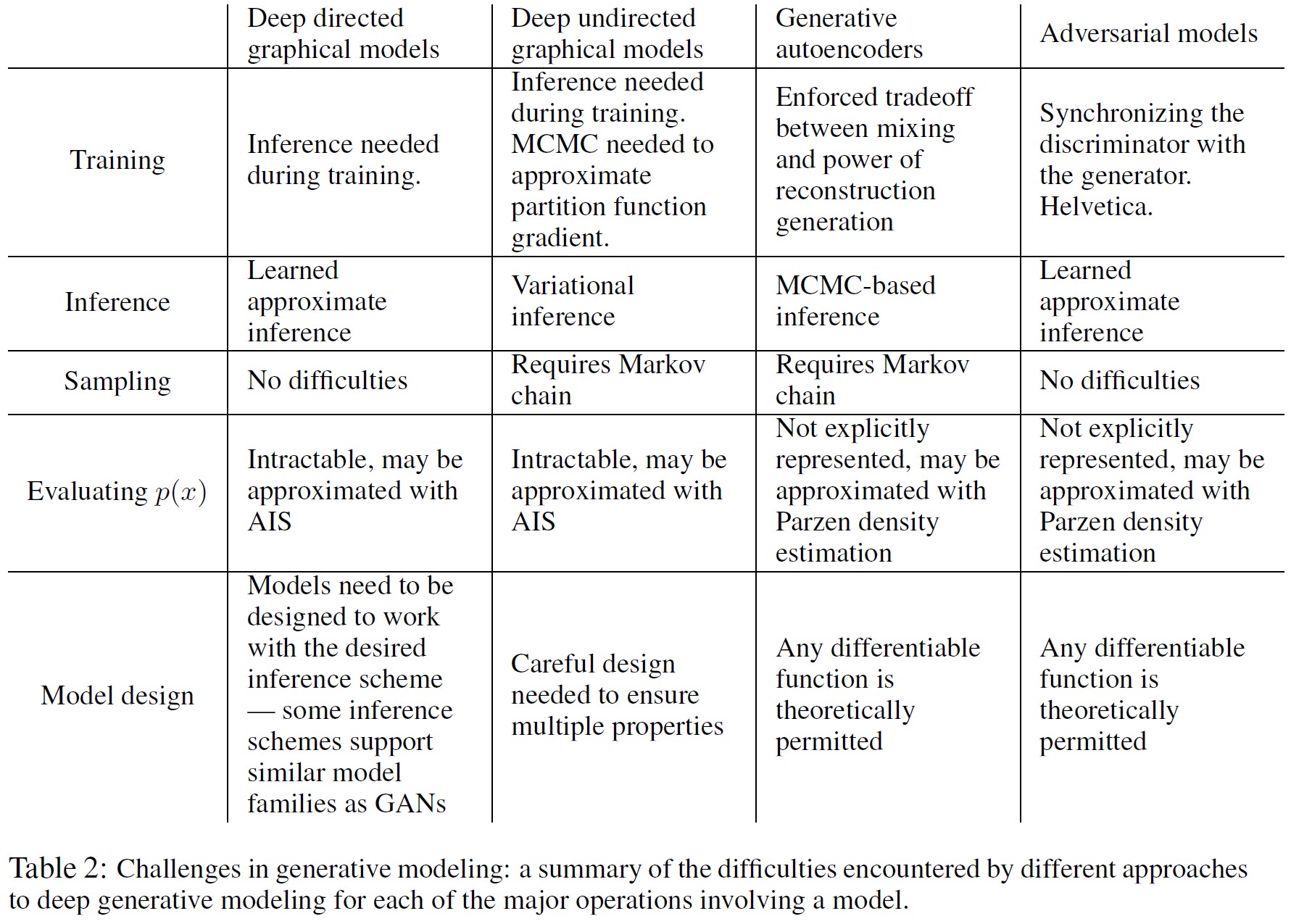
この新しいフレームワークには，これまでのモデリングフレームワークと比較して利点と欠点がある．

欠点は主に，\(p_g(x)\)の明示的な表現がないことと，学習中にDをGとうまく同期させなければならないことである（特に，\(p_{data}\)をモデル化するのに十分な多様性を持たせるために，Gが同じxの値に対してzの値を崩しすぎてしまう「ヘルベチカ・シナリオ」を避けるために，Dを更新せずにGを訓練しすぎてはならない）．

ボルツマンマシンの負の連鎖が，学習ステップの間に最新の状態に保たれなければならないのと同じである．

その利点は，マルコフ連鎖が不要であること，勾配を得るためにバックプロップのみが使用されること，学習中に推論が不要であること，そして多種多様な関数をモデルに組み込むことができることである．

表2は，生成的敵対ネットと他の生成的モデリングアプローチとの比較をまとめたものである．

前述の利点は主に計算上のものである．

逆説的モデルはまた，生成器ネットワークがデータ例によって直接更新されるのではなく，識別器を流れる勾配によってのみ更新されることによって，統計的な利点を得ることができる．

これは，入力の構成要素が直接生成器のパラメータにコピーされないことを意味する．

敵対的ネットワークのもう一つの利点は，マルコフ連鎖に基づく手法では，連鎖がモード間を混合できるようにするために，分布がある程度ぼやけている必要があるのに対して，敵対的ネットワークは非常にシャープで，縮退した分布さえも表現できることである．

7章：Conclusions and future work（結論と今後の課題）

このフレームワークは，多くの簡単な拡張が可能である．

1. 条件付き生成モデル\(p(x | c)\)は，GとDの両方に入力としてcを加えることで得られる．
2. 学習された近似推論は，xが与えられたときにzを予測する補助ネットワー クを訓練することで実行できる．これはwake-sleepアルゴリズム[15]によって訓練される推論ネットワークに似ているが，生成ネットワークの訓練が終了した後に，固定された生成ネットに対して推論ネットを訓練するかもしれないという利点がある．
3. パラメータを共有する条件モデルのファミリーを訓練することで，Sがxのインデックスの部分集合であるすべての条件式\(p(x_S | x_\$)\)を近似的にモデル化することができる．基本的には，決定論的MP-DBM[10]を確率的に拡張したものを実装するために，敵対的ネットワークを使うことができる．
4. 半教師付き学習：識別器や推論ネットからの特徴は，ラベル付きデータが限られている場合に分類器の性能を向上させることができる．
5. 効率の改善：GとDを調整するためのより良い方法を考案したり，訓練中にzをサンプリングするためのより良い分布を決定したりすることで，訓練を大幅に加速することができる．

本論文は，敵対的モデリングのフレームワークの実行可能性を実証し，これらの研究の方向性が有用であることを示唆した．

References（参考文献）

1. Bastien, F., Lamblin, P., Pascanu, R., Bergstra, J., Goodfellow, I. J., Bergeron, A., Bouchard, N., and Bengio, Y. (2012). Theano: new features and speed improvements. Deep Learning and Unsupervised Feature Learning NIPS 2012 Workshop.
2. Bengio, Y. (2009). Learning deep architectures for AI. Now Publishers.
3. Bengio, Y., Mesnil, G., Dauphin, Y., and Rifai, S. (2013). Better mixing via deep representations. In ICML’13.
4. Bengio, Y., Thibodeau-Laufer, E., and Yosinski, J. (2014a). Deep generative stochastic networks trainable by backprop. In ICML’14.
5. Bengio, Y., Thibodeau-Laufer, E., Alain, G., and Yosinski, J. (2014b). Deep generative stochastic networks trainable by backprop. In Proceedings of the 30th International Conference on Machine Learning (ICML’14).
6. Bergstra, J., Breuleux, O., Bastien, F., Lamblin, P., Pascanu, R., Desjardins, G., Turian, J., Warde-Farley, D., and Bengio, Y. (2010). Theano: a CPU and GPU math expression compiler. In Proceedings of the Python for Scientific Computing Conference (SciPy). Oral Presentation.
7. Breuleux, O., Bengio, Y., and Vincent, P. (2011). Quickly generating representative samples from an RBM-derived process. Neural Computation, 23(8), 2053–2073.
8. Glorot, X., Bordes, A., and Bengio, Y. (2011). Deep sparse rectifier neural networks. In AISTATS’2011.
9. Goodfellow, I. J., Warde-Farley, D., Mirza, M., Courville, A., and Bengio, Y. (2013a). Maxout networks. In ICML’2013.
10. Goodfellow, I. J., Mirza, M., Courville, A., and Bengio, Y. (2013b). Multi-prediction deep Boltzmann machines. In NIPS’2013.
11. Goodfellow, I. J., Warde-Farley, D., Lamblin, P., Dumoulin, V., Mirza, M., Pascanu, R., Bergstra, J., Bastien, F., and Bengio, Y. (2013c). Pylearn2: a machine learning research library. arXiv preprint arXiv:1308.4214.
12. Gregor, K., Danihelka, I., Mnih, A., Blundell, C., andWierstra, D. (2014). Deep autoregressive networks. In ICML’2014.
13. Gutmann, M. and Hyvarinen, A. (2010). Noise-contrastive estimation: A new estimation principle for unnormalized statistical models. In Proceedings of The Thirteenth International Conference on Artificial Intelligence and Statistics (AISTATS’10).
14. Hinton, G., Deng, L., Dahl, G. E., Mohamed, A., Jaitly, N., Senior, A., Vanhoucke, V., Nguyen, P., Sainath, T., and Kingsbury, B. (2012a). Deep neural networks for acoustic modeling in speech recognition. IEEE Signal Processing Magazine, 29(6), 82–97.
15. Hinton, G. E., Dayan, P., Frey, B. J., and Neal, R. M. (1995). The wake-sleep algorithm for unsupervised neural networks. Science, 268, 1558–1161.
16. Hinton, G. E., Srivastava, N., Krizhevsky, A., Sutskever, I., and Salakhutdinov, R. (2012b). Improving neural networks by preventing co-adaptation of feature detectors. Technical report, arXiv:1207.0580.
17. Jarrett, K., Kavukcuoglu, K., Ranzato, M., and LeCun, Y. (2009). What is the best multi-stage architecture for object recognition? In Proc. International Conference on Computer Vision (ICCV’09), pages 2146–2153. IEEE.
18. Kingma, D. P. and Welling, M. (2014). Auto-encoding variational bayes. In Proceedings of the International Conference on Learning Representations (ICLR).
19. Krizhevsky, A. and Hinton, G. (2009). Learning multiple layers of features from tiny images. Technical report, University of Toronto.
20. Krizhevsky, A., Sutskever, I., and Hinton, G. (2012). ImageNet classification with deep convolutional neural networks. In NIPS’2012.
21. LeCun, Y., Bottou, L., Bengio, Y., and Haffner, P. (1998). Gradient-based learning applied to document recognition. Proceedings of the IEEE, 86(11), 2278–2324.
22. Mnih, A. and Gregor, K. (2014). Neural variational inference and learning in belief networks. Technical report, arXiv preprint arXiv:1402.0030.
23. Rezende, D. J., Mohamed, S., and Wierstra, D. (2014). Stochastic backpropagation and approximate inference in deep generative models. Technical report, arXiv:1401.4082.
24. Rifai, S., Bengio, Y., Dauphin, Y., and Vincent, P. (2012). A generative process for sampling contractive auto-encoders. In ICML’12.
25. Salakhutdinov, R. and Hinton, G. E. (2009). Deep Boltzmann machines. In AISTATS’2009, pages 448–455.
26. Schmidhuber, J. (1992). Learning factorial codes by predictability minimization. Neural Computation, 4(6), 863–879.
27. Susskind, J., Anderson, A., and Hinton, G. E. (2010). The Toronto face dataset. Technical Report UTML TR 2010-001, U. Toronto.
28. Szegedy, C., Zaremba, W., Sutskever, I., Bruna, J., Erhan, D., Goodfellow, I. J., and Fergus, R. (2014). Intriguing properties of neural networks. ICLR, abs/1312.6199.
29. Tu, Z. (2007). Learning generative models via discriminative approaches. In Computer Vision and Pattern Recognition, 2007. CVPR’07. IEEE Conference on, pages 1–8. IEEE.

参考：Generative Adversarial Networksの解説スライド・動画

Generative Adversarial Networksの解説スライドです．

Generative Adversarial Networksの解説動画です．

まとめ

NeurIPS（旧NIPS）の論文「Generative Adversarial Networks」の日本語訳を紹介しました．

イアン・グッドフェローによる敵対的生成ネットワーク（GANs：Generative Adversarial Networks）がわかりました．

AIのプログラミング言語「C++/Python言語」を学べるおすすめのWebサイトを知りたいあなたはこちらからどうぞ．

独学が難しいあなたは，AIを学べるオンラインプログラミングスクール3社で自分に合うスクールを見つけましょう．後悔はさせません！

国内・海外のAIエンジニアのおすすめ求人サイトを知りたいあなたはこちらからどうぞ．

国内・海外のプロンプトエンジニアのおすすめ求人サイトを知りたいあなたはこちらからどうぞ．