【第32回】元東大教員から学ぶリアルタイムシステム「Stack Resource Policy」

本記事の信頼性

リアルタイムシステムの研究歴12年．
東大教員の時に，英語でOS（Linuxカーネル）の授業．
2012年9月～2013年8月にアメリカのノースカロライナ大学チャペルヒル校（UNC）コンピュータサイエンス学部で客員研究員として勤務．C言語でリアルタイムLinuxの研究開発．
プログラミング歴15年以上，習得している言語: C/C++，Python，Solidity/Vyper，Java，Ruby，Go，Rust，D，HTML/CSS/JS/PHP，MATLAB，Verse（UEFN）, Assembler (x64，ARM)．
東大教員の時に，C++言語で開発した「LLVMコンパイラの拡張」，C言語で開発した独自のリアルタイムOS「Mcube Kernel」をGitHubにオープンソースとして公開．
2020年1月～現在はアメリカのノースカロライナ州チャペルヒルにあるGuarantee Happiness LLCのCTOとしてECサイト開発やWeb/SNSマーケティングの業務．2022年6月～現在はアメリカのノースカロライナ州チャペルヒルにあるJapanese Tar Heel, Inc.のCEO兼CTO．
最近は自然言語処理AIとイーサリアムに関する有益な情報発信に従事．

（AI全般を含む）自然言語処理AIの論文の日本語訳や，AIチャットボット（ChatGPT，Auto-GPT，Gemini（旧Bard）など）の記事を50本以上執筆．アメリカのサンフランシスコ（広義のシリコンバレー）の会社でプロンプトエンジニア・マネージャー・Quality Assurance（QA）の業務委託の経験あり．
（スマートコントラクトのプログラミングを含む）イーサリアムや仮想通貨全般の記事を200本以上執筆．イギリスのロンドンの会社で仮想通貨の英語の記事を日本語に翻訳する業務委託の経験あり．

こういった私から学べます．

前回を読んでいない方はこちらからどうぞ．

: 【第31回】元東大教員から学ぶリアルタイムシステム「Priority Ceiling Protocol」

こういった私から学べます．前回を読んでいない方はこちらからどうぞ．リアルタイムシステムの記事一覧はこちらからどうぞ． Priority Ceiling Protocol（PCP） Priority ...

続きを見る

リアルタイムシステムの記事一覧はこちらからどうぞ．

: 元東大教員から学ぶリアルタイムシステム

こういった私から学べます．リアルタイムシステムとは，決められた時間（デッドライン）までに処理を完了しなければならない性質をもつシステムのことです．リアルタイムシステムは，ロボット，自動車や航空機な ...

続きを見る

リアルタイムシステムで使われているリアルタイムOSは，主にC言語で書かれています．

私にC言語の無料相談をしたいあなたは，公式LINE「ChishiroのC言語」の友だち追加をお願い致します．

私のキャパシティもあり，一定数に達したら終了しますので，今すぐ追加しましょう！

独学が難しいあなたは，元東大教員がおすすめするC言語を学べるオンラインプログラミングスクール5社で自分に合うスクールを見つけましょう．後悔はさせません！

: 元東大教員がおすすめするC言語を学べるオンラインプログラミングスクール5社

こういった悩みにお答えします．こういった私が解説していきます．私が大学の授業で初めてC言語を勉強した時は全然できませんでしたが，先生やTA，友人に相談しながら一生懸命C言語を勉強してできるようにな ...

続きを見る

Stack Resource Policy（SRP）

Stack Resource Policy（SRP）は，Bakerにより提案された共有資源へのアクセスのための手法です．

SRPは，3つの本質的な点でPriority Ceiling Protocol（PCP）を拡張します．

複数ユニットの資源を利用可能
動的優先度スケジューリングのサポート
ランタイム（実行時の）スタックベースの資源を共有可能

スケジューリングの観点から見ると，PCPとSRPの間にある本質的な違いは，タスクがブロックされる時間帯です．

PCPでは，タスクは最初の資源要求をするときにブロックされるのに対し，SRPでは，タスクはプリエンプションしようとするときにブロックされます．

このように早期にブロックすることで，並行性はわずかに低下しますが，不要なコンテキストスイッチの節約，プロトコルの実装の簡略化，ランタイムスタック資源の共有が可能になります．

※並行性とはCPUのアイドル時間を少なくし，効率的に利用できる性質のこと

SRPで使う用語の定義

SRPの正式な記述を紹介する前に，以下の用語の定義を紹介します．

優先度

各々のタスク$\tau_i$には，システム内の他のタスクに対する$\tau_i$の重要度（つまり緊急性）を示す優先度$p_i$が割り当てられます．

優先度は，静的または動的にタスクに割り当てることができます．

どの時点$t$でも，$p_a > p_b$は$\tau_a$の実行が$\tau_b$の実行よりも重要であることを意味します．

したがって，$\tau_b$は$\tau_a$に代わって遅らせることができます．

例えば，Rate Monotonic（RM）やEarliest Deadline First（EDF）に基づいてタスクに優先度を割り当てることができます．

プリエンプションレベル

優先度$p_i$の他に，タスク$\tau_i$はプリエンプションレベル$\pi_i$によっても特徴づけられます．

プリエンプションレベルは静的パラメータで，タスクの作成時にタスクに割り当てられ，そのタスクのすべてのインスタンスに関連付けられます．

プリエンプションレベルの本質的な性質は，あるタスク$\tau_a$は$\pi_a > \pi_b$の場合にのみ，別のタスク$\tau_b$をプリエンプションできるということです．

これは優先度にも当てはまります．

したがって，プリエンプションレベルと優先度を区別する理由は，プリエンプションレベルは固定値であり，動的優先度スキームの存在下でも潜在的なブロッキングを予測するために利用できるからです．

SRPのすべての特性を証明するために利用されるプリエンプションレベルの一般的な定義は，「$\tau_a$が$\tau_b$の後に到着し，$\tau_a$が$\tau_b$よりも優先度が高い場合，$\tau_a$は$\tau_b$よりも高いプリエンプションレベルを持っていなければならないこと」を要求します．

EDFスケジューリングでは，プリエンプションレベルが相対デッドラインの降順の逆順（つまり，プリエンプションレベルの昇順）になる場合，前の条件が満たされます．

$$\pi_i > \pi_j \Longleftrightarrow D_i < D_j$$

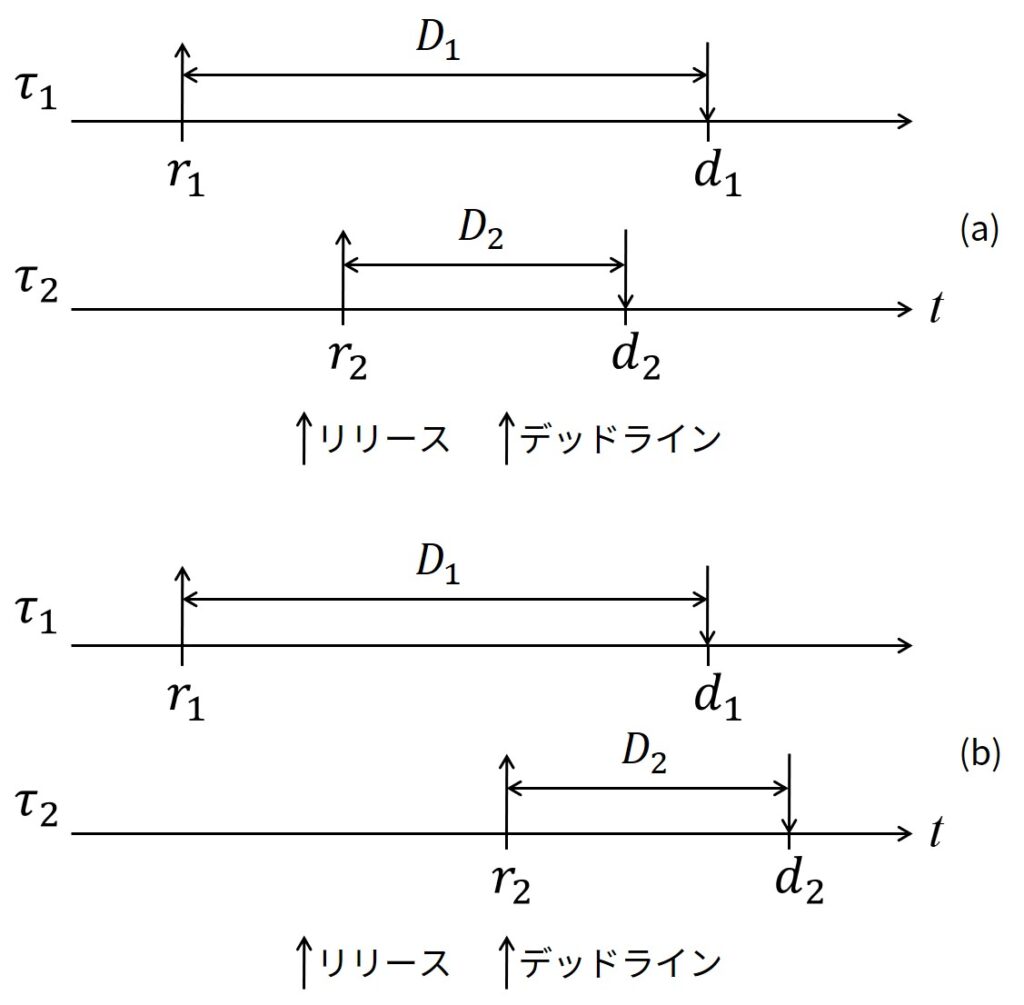
Difference between Priorities and Premption Levels

優先度とプリエンプションレベルの違いをよりよく説明するために，上図に示す例を考えてみましょう．

ここでは，2つのタスク$\tau_1$と$\tau_2$があり，それぞれの相対デッドラインは$D_1 = 10$と$D_2 = 5$とします．

$D_2 < D_1$であるから，$\pi_1 = 1$，$\pi_2 = 2$と定義します．

$\pi_1 < \pi_2$なので，$\tau_1$は$\tau_2$をプリエンプションできません．

しかし，$\tau_1$は$\tau_2$よりも優先度が高い場合があります．

実際，EDFの下では，タスクの優先度は絶対デッドラインに基づいて動的に割り当てられます．

例えば，上図（a）に示されたケースでは，絶対デッドラインは$d_2 < d_1$の関係になります．

したがって，$\tau_2$は$\tau_1$よりも優先度が高くなります．

一方，上図（b）に示すように，$\tau_2$が時刻$r_1 + 6$に到着した場合，絶対デッドラインは$d_2 > d_1$となります．

したがって，$\tau_1$は$\tau_2$よりも優先度が高くなります．

$\tau_1$は$\tau_2$よりも優先度が高いが，$\tau_2$をプリエンプションできないことに注意して下さい．

これは，$d_1 < d_2$で$D_1 > D_2$の場合，$\tau_1$は常に$\tau_2$よりも前に始まるからです．

したがって，$\tau_2$をプリエンプションする必要はありません．

以下では，$i < j \Longleftrightarrow \pi_i > \pi_j$となるように，タスクをプリエンプションレベルの降順に並べることを想定しています．

これはまた，$D_1 < D_2 < ... < D_n$を意味します．

資源ユニット

各々の資源$R_k$は，複数のタスクが同時にアクセス可能な$N_k$ユニットを持つことが許されています．

この概念は，古典的な単一ユニット資源を一般化したもので，排他制御の下では一度に1つのタスクからアクセスできます．

各々のタスクが1ユニットを必要とする場合，$N_k$個のユニットを持つ資源は，$N_k$個の異なるタスクが同時にアクセスできます．

一般に，$n_k$は，$R_k$に対して現在利用可能なユニットの数を表し，$N_k - n_k$のユニットがロックされていることを意味します．

$n_k = 0$の場合，3ユニットの$R_k$を必要とするタスクは，$n_k$が3以上になるまでブロックされます．

資源要求

マルチユニットセマフォ$S_k$により保護されたクリティカルセクション$z_{i,k}$に入る時，タスク $\tau_i$ は $wait(S_k, r)$ を呼び出して必要なユニット数$r$を指定しなければなりません．

クリティカルセクションを出る時，$\tau_i$は$signal(S_k)$を呼び出して，すべての$r$を解放しなければなりません．

$\tau_i$が$R_k$に対して同時に要求できる最大単位数は$\mu_i (R_k)$で表され，これはタスクコードを解析することによりオフラインで（実行前に）導出できます．

$\tau_i$が利用可能なユニットよりも多くのユニットを必要とする場合，すなわち，$\mu_i (R_k) > n_k$であれば， $n_k$が$\mu_i (R_k)$以上になるまで$\tau_i$はブロックすることは明らかです．

資源上限

各々の資源$R_k$（またはセマフォ$S_k$）には，最大リクエストを発行した場合に$R_k$上でブロックされる可能性のあるタスクの最高のプリエンプションレベルに等しい上限$C_{R_k} (n_k)$が割り当てられます．

したがって，資源の上限は動的な値であり，これは現在利用可能なユニット$R_k$の関数です．

$$C_{R_k} (n_k) = \max \{ \pi_i \ | \ \mu_i (R_k) > n_k \}$$

$R_k$のすべてのユニットが利用可能であれば，すなわち，$n_k = N_k$であれば，$C_{R_k} (N_k) = 0$です．

タスク	$D_i$	$\pi_i$	$\mu_i (R_1)$	$\mu_i (R_2)$	$\mu_i (R_3)$
$\tau_1$	5	3	1	0	1
$\tau_2$	10	2	2	1	3
$\tau_3$	20	1	3	1	1

この概念をより明確にするために，3つのタスク（$\tau_1$，$\tau_2$，$\tau_3$）が，それぞれ3つ，1つ，3つのユニットで構成されている3つの資源（$R_1$，$R_2$，$R_3$）を共有している場合の例を考えてみましょう．

すべてのタスクのパラメータ（相対デッドライン，プリエンプションレベル，資源要求）を上表に示します．

資源	$C_R (3)$	$C_R (2)$	$C_R (1)$	$C_R (0)$
$R_1$	0	1	2	3
$R_2$	-	-	0	2
$R_3$	0	2	2	3

これらの要件に基づき，利用可能なユニット数$n_k$の関数としての資源の現在の上限を上表に示します（ダッシュ「-」は不可能な場合を示します）．

例えば，資源$R_1$が3つのうち2つしかない場合の上限を算出してみましょう．

1番目の表から，この条件でブロックされる可能性のあるタスクは，$R_1$を3個必要とするため，$\tau_3$だけであることがわかります．

したがって，$C_{R_1} (2) = \pi_3 = 1$となります．

もし$R_1$がたった1ユニットしかない場合，ブロックされる可能性のあるタスクは$\tau_2$と$\tau_3$です．

したがって，$C_{R_1} (1) = \max (\pi_2, \pi_3) = 2$となります．

最後に，$R_1$のユニットが1つもない場合は，3つのタスクをすべて$R_1$でブロックできます．

したがって，$C_{R_1} (0) = \max (\pi_1, \pi_2, \pi_3) = 3$となります．

システム上限

SRPで採用されている資源アクセスプロトコルでは，すべての資源の現在の上限の最大値として定義されたシステムの上限$\prod_s$も必要とします．

$$\prod_s = \underset{k}{\max} \{ C_{R_k} \}$$

$\prod_s$は動的パラメータであり，タスクが資源にアクセスしたり解放したりするたびに変更されることに注意してください．

SRPの定義

SRPの重要なアイデアは，タスクが利用できない資源を必要としているときに，後からではなくプリエンプションしようとした時点でブロックされるということです．

さらに，複数の優先度逆転を防ぐために，現在利用可能な資源が，それをプリエンプションする可能性のあるすべてのタスクの最大要件を満たすのに十分な量になるまで，タスクを開始できません．

最初に紹介した定義を用いて，次のようなプリエンプションテストを行うことで実現します．

SRPのプリエンプションテスト

タスクは，実行可能なすべてのタスクの中の最高優先度で，そのプリエンプションレベルがシステムの上限よりも高くなるまで，プリエンプションできません．

もしレディキューが優先度の降順に並べられている場合，最高優先度のレディタスク（キューの先頭にあるもの）のプリエンプションレベル$\pi (r)$をシステムの上限と比較することで，プリエンプションテストを簡単に実行できます．

もし$\pi (r) > \prod_s$の場合，タスク$\tau$が実行され，それ以外の場合は$\prod_s$が$\pi (r)$より小さくなるまでレディキューに保持されます．

条件$\pi_r > \prod_s$は，$\prod_s$が減少するかもしれない時，つまり資源が解放される時はいつでもテストされなければなりません．

SRPの観察

SRPの利用がタスクの実行に及ぼす影響は，以下の観察を通してよりよく理解できます．

タスク$\tau$のプリエンプションテストに合格すると，現在利用可能な資源は，タスク$\tau$の最大要件と$\tau$をプリエンプションする可能性のあるすべてのタスクの最大要件を満たすのに十分であることが保証されます．
これは，一度$\tau$が実行を開始すると，資源競合のためにブロックされないことを意味します．
タスクのプリエンプションテストは$\tau$が実行を開始する前に行われますが，この時には資源は割り当てられず，要求された時にのみ割り当てられます．
資源を必要としないタスクであっても，プリエンプションテストによりブロックされることがあります．
これは，上限がない優先度逆転を避けるために必要です．
アクセス時ではなくプリエンプション時にブロッキングすると，より悲観的になり，（HLPの場合のように）不必要なブロッキングが発生する可能性がありますが，コンテキストスイッチの数を減らし，ランタイム（実行時の）オーバーヘッドを減らし，プロトコルの実装を簡素化します．
プリエンプションテストは，優先度継承を課す効果があります．
つまり，資源を保持している実行タスクはシステムの上限を変更し，その資源を必要とする可能性のあるタスクの優先度を継承しているかのようにプリエンプションに抵抗します．
この効果は，タスクの優先度を変更することなく達成されることに注意してください．

SRPのスケジュール例

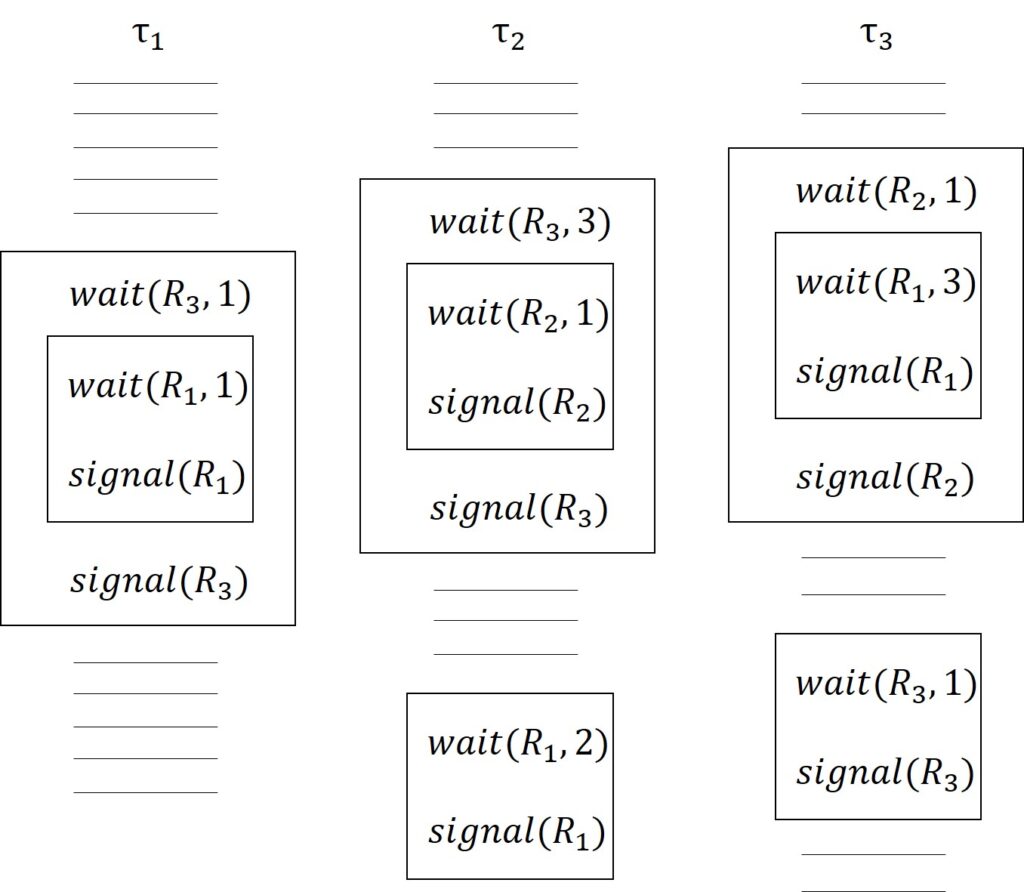
SRPがどのように動作するかを説明するために，1番目の表で説明したタスクセットを考えてみましょう．

タスクの構造を上図に示します．

ここで，$wait(R_k, r)$は資源$R_k$の$r$ユニットの要求を，$signal(R_k)$はその解放を表します．

資源の現在の上限はすでに2番目の表に示されており，このタスクセットの可能なEDFスケジュールは下図に示します．

この図では，4番目のタイムラインでシステム上限の変動を記載し，スケジュールに沿った数字は資源IDを表しています．

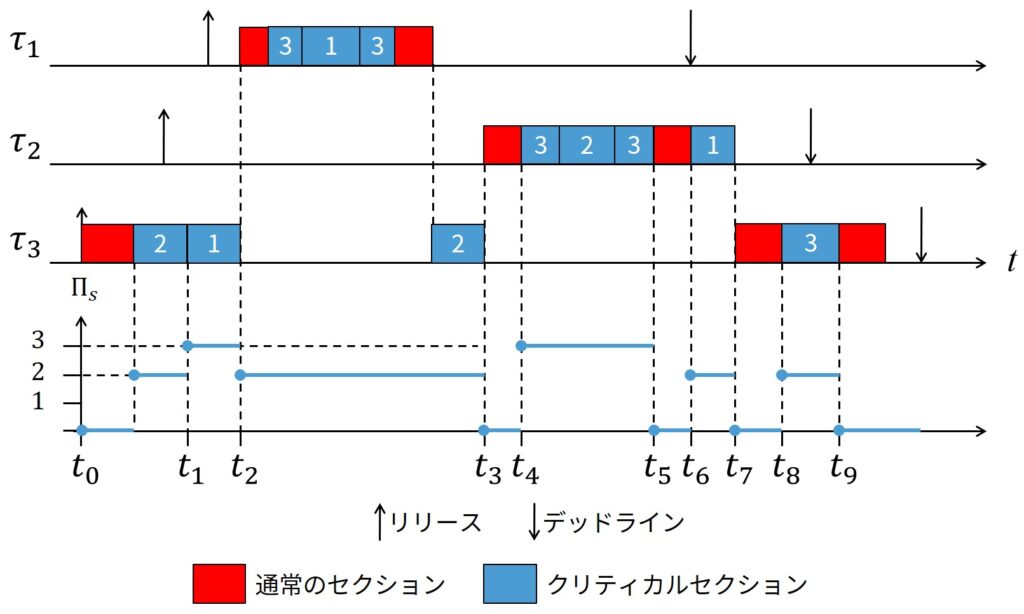
時刻$t_0$で，$\tau_3$は実行を開始し，すべての資源が完全に利用可能なため，システムの上限はゼロになります．

$\tau_3$が最初のクリティカルセクションに入ると，$R_2$の唯一のユニットを取ります．

したがって，システムの上限は，$R_2$でブロックされる可能性のあるタスクの中で最も高いプリエンプションレベルに設定されています（2番目の表参照）．

つまり，$\prod_s = \pi_2 = 2$となります．

結果として，$\tau_2$はプリエンプションテストによってブロックされ，$\tau_3$は実行を継続します．

$\tau_3$がそのネストしたクリティカルセクションに入ると（$R_1$の全ユニットを取ると），システムの上限が$\prod_s = \pi_1 = 3$に上昇することに注意してください．

これにより，プリエンプションテストにより$\tau_1$がブロックされます．

（時刻$t_2$で）$\tau_3$が$R_1$を解放すると，システムの上限が$s=2$になります．

したがって，$\tau_1$は$\tau_3$をプリエンプションして実行を開始します．

$\tau_1$が一度実行開始すると，実行中にブロックされることはないことに注意してください．

なぜなら，条件$\pi_1 > \prod_s$は，$\tau_1$が必要とするすべての資源が利用可能であることを保証するからです．

$\tau_1$が終了すると，$\tau_3$は実行を再開し，資源$R_2$を解放します．

$R_2$が解放されると，システム上限がゼロに戻り，$\tau_2$は$\tau_3$をプリエンプションできます．

繰り返しになりますが，いったん$\tau_2$が実行開始すると，それが必要とするすべての資源が利用可能になります．

したがって，$\tau_2$は決してブロックされません．

SRPの性質

ここでは，SRPの主な性質を紹介します．

これらは，スケジュール可能性解析と各々のタスクの最長ブロッキング時間の算出に利用されます．

補題32.1：タスクのプリエンプションレベルが資源$R$の現在の上限よりも高い場合，以下の2つを満たす利用可能な$R$のユニットが十分に存在する．

タスクの最大要件を満たすこと
タスクをプリエンプションできるすべてのタスクの最大要件を満たすこと

証明：$\pi (\tau) > C_R$で，$R$に対する$\tau$の最大要求が満たされないと仮定します．

資源の現在の上限の定義では，$C_R \geq \pi (\tau)$となり，これは矛盾しています．

仮に$\pi (\tau) > C_R$と仮定しますが，$R$に対する$\tau_H$の最大要求を満たせないような$\tau$をプリエプション可能なタスク$\tau_H$が存在するとします．

$\tau_H$は$\tau$をプリエプションできるので，$\pi (\tau_H) > \pi (\tau)$でなければなりません．

また，$R$に対する$\tau_H$の最大要求を満たせないので，資源の現在の上限を定義すると， $C_R \geq \pi (\tau_H) > \pi (\tau)$となり，仮定に反します．□

定理32.1：もし，$\pi (\tau) > \prod_s$までタスク$\tau$の実行が許可されていない場合，タスクが開始してからブロックされることはない．

証明：タスク$\tau$をプリエプションできるタスク数を$N$とし，プリエプションレベルが$s$より大きくなるまではどのタスクも実行できないと仮定します．

$N$に対する帰納法で証明します．

$N = 0$の場合，プリエプションできるタスクはありません．

もし$\pi (\tau) > \prod_s$の時に$\tau$が開始する場合，補題32.1は，$\tau$により必要とされるすべての資源が，$\tau$がプリエプションした時に利用可能であることを保証します．

したがって，タスクはブロックされることなく終了まで実行します．

もし$N > 0$の場合，$\tau$が$\tau_H$によりプリエンプションされるとします．

$\pi (\tau_H) > \prod_s$のときに$\tau_H$が開始する場合，$\tau_H$がプリエンプションしたときに$\tau_H$が必要とするすべての資源が利用可能であることを保証します．

$\tau_H$をプリエンプションするあらゆるタスクは$\tau$もプリエンプションするので，帰納仮定（Induction Hypothesis）は，$\tau_H$をプリエンプションするタスクと同様に，$\tau_H$がブロッキングすることなく終了まで実行することを保証します．

$\tau$をプリエンプションした全てのタスクが終了すると，$\tau$はブロックせずに実行を再開できます．

高優先度タスクがすべての資源を解放し，$\tau$が起動したときに利用可能な資源が$\tau$の最大リクエストを満たすのに十分だったからです．□

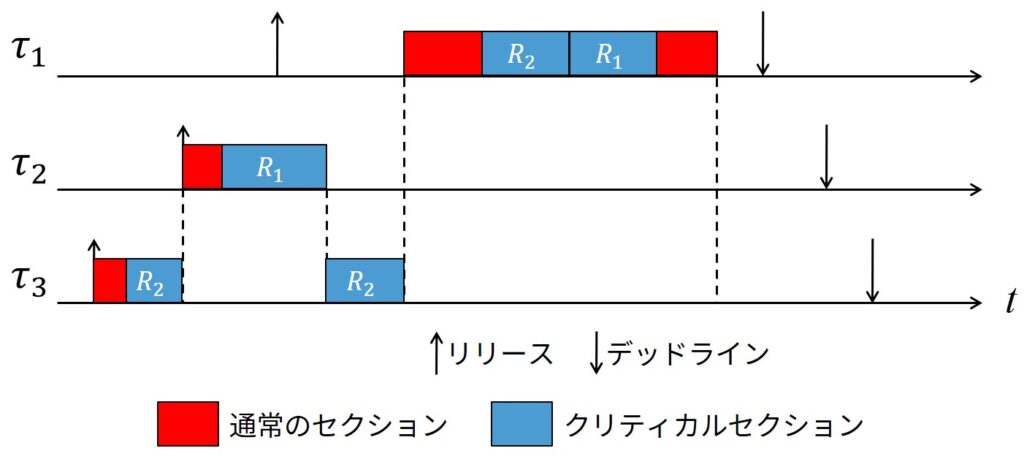
Absurd Situation that Cannot Occur Under SRP

定理32.2：SRPの下では，タスク$\tau_i$は最大でも 1 つのクリティカルセクションの間ブロックできる．

証明：$\tau_i$が2つの低優先度タスク$\tau_1$と$\tau_2$に共有されている2つのクリティカルセクションの間ブロックされていると仮定します．

一般性を損なうことなく，$\pi_2 < \pi_1 < \pi_i$と仮定します．

これは，（$R_1$と$R_2$のような）$\tau_1$と$\tau_2$が2つの異なる資源を保持していて，$\tau_2$がそのクリティカルセクション内で$\tau_1$によりプリエンプションされている場合にのみ起こります．

この状況を上図に示します．これはすぐに矛盾を生みます．

実際には，$\tau_1$はプリエンプションテストによりブロックされていないので，$\pi_1 > \prod_s$となります．

一方，$\tau_i$はブロックされているので，$\pi_i \leq \prod_s$となります．

したがって，$\pi_i < \pi_1$となり，この仮定は矛盾しています．□

定理32.3：SRPはデッドロックを防ぐ．

証明：定理32.1では，タスクが起動した後にブロックできません．

資源を保持している間はタスクをブロックできないので，デッドロックは発生しません．

SRPにおけるタスクのブロック時間の算出

タスクがSRPで経験できる最長ブロッキング時間は，PCPと同じです．

実際，定理32.2は，SRPの下では，タスク$\tau_i$をブロックできるものの中で，最大で1つのクリティカルセクションの期間だけタスク$\tau_i$をブロックできることを保証しています．

PCPについて証明された補題31.3は，SRPに簡単に拡張できます．

したがって，タスク$\tau_j$に属し，セマフォ$S_k$で保護されているクリティカルセクション $Z_{j,k}$ は，$\pi_j < \pi_i$と$\max(C_{S_k}) \geq \pi_i$の場合にのみ，タスク$\tau_i$をブロックできます．

SRPの下では，セマフォの上限は動的な変数なので，その最大値（つまり，現在利用可能なユニット数が0に等しいものに対応するもの）を考慮しなければならないことに注意してください．

したがって，タスク$\tau_i$は，$\pi_i$未満のプリエンプションレベルを持つタスクに属するクリティカルセクションと，$\pi_i$以上の最大上限を持つセマフォによって保護されたクリティカルセクションによってのみブロックされます．

$$\gamma_i = \{ Z_{j,k}\ | \ (\pi_j < \pi_i) {\rm \ and \ } C_{S_k} (0) \geq \pi_i \}$$

そして，$\tau_i$は最大でも1回ブロックされるので，$\tau_i$が被る最長ブロック時間は，$\tau_i$をブロックできるものの中で最長クリティカルセクションの持続時間で与えられます．

$$B_i = \underset{j,k}{\max} \{ \delta_{j,k} - 1\ | \ Z_{j,k} \in \gamma_i \}$$

SRPにおけるランタイムスタックの共有

SRPの利用から得られるもう一つの興味深い意味は，タスク間のスタック共有をサポートしていることです．

特に，多数のタスクで構成されるアプリケーションでは，取得，監視，制御活動に特化したものが便利です．

従来のOSでは，各々のプロセスはコンテキスト（つまり，CPUレジスタの内容）とローカル変数を格納するのにプライベートなスタック空間を持たなければなりません．

これらのシステムの問題点は，タスク数が多い場合，すべてのタスクのスタックに大量のメモリが必要になることです．

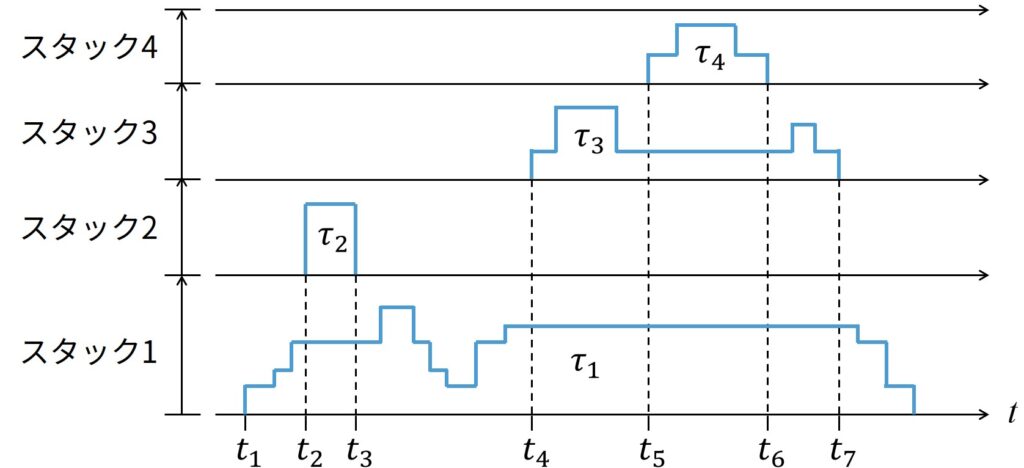
Possible Evolution with One Stack per Task

例えば，4つのタスク$\tau_1$，$\tau_2$，$\tau_3$，$\tau_4$で，それぞれのプリエンプションレベルは，1，2，2，3（プリエンプションレベル3が最高プリエンプションレベル）を考えてみましょう．

上図は，各々のタスクの最大要件に等しい自分のスタック空間が割り当てられていると仮定した場合のスタックの推移を示します．

時刻$t_1$で$\tau_1$が実行を開始し，時刻$t_2$で$\tau_2$がプリエンプションし，時刻$t_3$で終了し，$\tau_1$が再開できます．

時刻$t_4$では，$\tau_1$は$\tau_3$によりプリエンプションされ，$\tau_4$は時刻$t_5$でプリエンプションされます．

時刻$t_6$で$\tau_4$が終了し，$\tau_3$が再開します．

時刻$t_7$で$\tau_3$が終了し，$\tau_1$が再開します．

各々のプロセススタックの先頭はプロセス実行中に変化しますが，各々のスタックのために予約されたストレージ領域は一定であり，2本の水平線の間の距離に対応していることに注意してください．

このケースでは，アプリケーションのために予約しなければならないストレージ領域の合計は，各々のプロセスに専用のスタック領域の合計に等しいです．

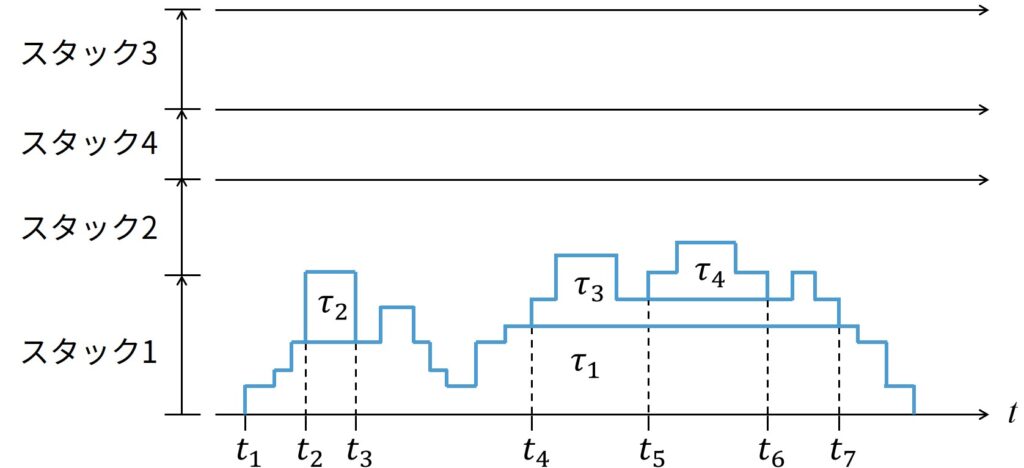
Possible Evolution with Single Task for All Tasks

しかし，すべてのタスクが独立していたり，共有資源にアクセスするためにSRPを利用している場合，それらのタスクは1つのスタック空間を共有できます．

このケースでは，あるタスク$\tau$があるタスク$\tau'$にプリエンプションされた場合，$\tau$はそのスタックを維持し，$\tau'$のスタックは$\tau$のスタックのすぐ上に割り当てられます．

上図は，すべてのタスクに1つのスタックが割り当てられている時の，以前のタスクセットの展開を示しています．

SRPの下では，相互侵入を伴わないスタックのオーバーラップは，定理32.1の直接の結果です．

実際には，タスク$\tau$は一度起動するとブロックされないので，そのスタックは，より低いプリエンプションレベルのタスクに属するものには決して侵入できず，$\tau$が終了した後にのみ再開できます．

上の2本の水平線の間のスタック空間（これは$\tau_2$と$\tau_3$の間の最小スタックに相当する）は不要になったことに注意してください．

$\tau_2$と$\tau_3$は同じプリエンプションレベルを持っているので，スタックス空間を同時に占有できません．

一般的に，同じプリエンプションレベルのタスク数が多いほど，スタックの消費量が少なくなります．

例えば，100個のタスクが10個のプリエンプションレベルに分散され，各々のレベルに10個のタスクがあるアプリケーションを考えてみましょう．

各々のタスクが最大10Kバイトのスタック空間を必要とします．

タスクごとにスタックを利用すると，1000Kバイトが必要になります．

逆にシングルスタックを利用すると，プリエンプションレベルごとに1つ以上のタスクを一度にアクティブにすることができないので，100Kバイトだけで十分です．

したがって，この例では900Kバイト（つまり，90%）を節約することができます．

一般的に，タスクが$k$個のプリエンプションレベルに分散されている場合，1つのスタックに必要な空間は，各々のレベルの最大リクエストの合計に等しい．

SRPの実装に関する考察

SRPの実装はPCPと似ていますが，ロック操作（$srp\_wait$と$srp\_signal$）はよりシンプルで，セマフォをロックしようとしたときにタスクがブロックされることはありません．

タスクの最大要件を満たすのに十分な資源がない場合，そのタスクはプリエンプションを許可せず，レディキューに保持されます．

プリエンプションテストを簡単にするために，（利用可能なユニットの数に関わらず）資源のすべての上限を事前に算出し，テーブルに格納します．

さらに，スタックを利用することで，システムの上限を把握できます．

資源$R$が割り当てられると，その現在の状態である$n_R$が更新され，$C_R (n_R) > \prod_s$であれば，$\prod_s$に $C_R (n_R)$を設定します．

$n_R$と$\prod_s$の古い値はスタックにプッシュされます．

資源$R$が解放されると，スタックから$\prod_s$と$n_R$の値が復元されます．

復元されたシステム上限が前回の値よりも低い場合は，最高優先度のレディタスクに対してプリエンプションテストを実行し，プリエンプション可能かどうかを確認します．

プリエンプションテストに合格した場合，コンテキストスイッチが実行されます．

そうでなければ，現在のタスクの実行を継続します．

まとめ

今回はStack Resource Policy（SRP）を紹介しました．

具体的には，以下の内容を解説しました．

SRPの特徴
SRPで使う用語の定義
SRPの定義
SRPの性質
SRPにおけるタスクのブロック時間の算出
SRPにおける実行時のスタックの共有
SRPの実装に関する考察