【第31回】元東大教員から学ぶリアルタイムシステム「Priority Ceiling Protocol」

本記事の信頼性

リアルタイムシステムの研究歴12年．
東大教員の時に，英語でOS（Linuxカーネル）の授業．
2012年9月～2013年8月にアメリカのノースカロライナ大学チャペルヒル校（UNC）コンピュータサイエンス学部で客員研究員として勤務．C言語でリアルタイムLinuxの研究開発．
プログラミング歴15年以上，習得している言語: C/C++，Python，Solidity/Vyper，Java，Ruby，Go，Rust，D，HTML/CSS/JS/PHP，MATLAB，Verse（UEFN）, Assembler (x64，ARM)．
東大教員の時に，C++言語で開発した「LLVMコンパイラの拡張」，C言語で開発した独自のリアルタイムOS「Mcube Kernel」をGitHubにオープンソースとして公開．
2020年1月～現在はアメリカのノースカロライナ州チャペルヒルにあるGuarantee Happiness LLCのCTOとしてECサイト開発やWeb/SNSマーケティングの業務．2022年6月～現在はアメリカのノースカロライナ州チャペルヒルにあるJapanese Tar Heel, Inc.のCEO兼CTO．
最近は自然言語処理AIとイーサリアムに関する有益な情報発信に従事．

（AI全般を含む）自然言語処理AIの論文の日本語訳や，AIチャットボット（ChatGPT，Auto-GPT，Gemini（旧Bard）など）の記事を50本以上執筆．アメリカのサンフランシスコ（広義のシリコンバレー）の会社でプロンプトエンジニア・マネージャー・Quality Assurance（QA）の業務委託の経験あり．
（スマートコントラクトのプログラミングを含む）イーサリアムや仮想通貨全般の記事を200本以上執筆．イギリスのロンドンの会社で仮想通貨の英語の記事を日本語に翻訳する業務委託の経験あり．

こういった私から学べます．

前回を読んでいない方はこちらからどうぞ．

: 【第30回】元東大教員から学ぶリアルタイムシステム「Priority Inheritance Protocol」

こういった私から学べます．前回を読んでいない方はこちらからどうぞ．リアルタイムシステムの記事一覧はこちらからどうぞ． Priority Inheritance Protocol（PIP） Prio ...

続きを見る

リアルタイムシステムの記事一覧はこちらからどうぞ．

: 元東大教員から学ぶリアルタイムシステム

こういった私から学べます．リアルタイムシステムとは，決められた時間（デッドライン）までに処理を完了しなければならない性質をもつシステムのことです．リアルタイムシステムは，ロボット，自動車や航空機な ...

続きを見る

リアルタイムシステムで使われているリアルタイムOSは，主にC言語で書かれています．

私にC言語の無料相談をしたいあなたは，公式LINE「ChishiroのC言語」の友だち追加をお願い致します．

私のキャパシティもあり，一定数に達したら終了しますので，今すぐ追加しましょう！

独学が難しいあなたは，元東大教員がおすすめするC言語を学べるオンラインプログラミングスクール5社で自分に合うスクールを見つけましょう．後悔はさせません！

: 元東大教員がおすすめするC言語を学べるオンラインプログラミングスクール5社

こういった悩みにお答えします．こういった私が解説していきます．私が大学の授業で初めてC言語を勉強した時は全然できませんでしたが，先生やTA，友人に相談しながら一生懸命C言語を勉強してできるようにな ...

続きを見る

Priority Ceiling Protocol（PCP）

Priority Ceiling Protocol（PCP）は，優先度逆転問題を制限し，Chain BlockingやDeadlockを防ぐために提案されました．

PCPの基本的なアイデアは，空いているセマフォ上のロック要求を許可するためのルールを持つPriority Inheritance Protocol（PIP）を拡張することです．

複数のブロックを避けるために，このルールでは，ブロックする可能性のあるロックされたセマフォがある場合，タスクがクリティカルセクションに入ることを許可しません．

これは，タスクが最初のクリティカルセクションに入ると，そのタスクが完了するまで，低優先度タスクにブロックされないことを意味します．

このアイデアを実現するために，各々のセマフォには，セマフォをロックできるタスクの中で最高優先度に等しい優先度上限（Priority Ceiling）が割り当てられます．

そして，タスク$\tau_i$は，その優先度が$\tau_i$以外のタスクにより現在ロックされているセマフォのすべての優先度上限よりも高い場合にのみ，クリティカルセクションに入ることが許可されます．

PCPの定義

PCPの定義は以下になります．

各々のセマフォ$S_k$には，それをロックできるタスクの中で最高優先度に等しい優先度上限$C(S_k)$が割り当てられます．
$C(S_k)$はオフライン（実行前に）に算出できる静的な値であることに注意してください．
$$C(S_k) \overset{\rm def}{=} \underset{i}{\max} \{ P_i \ | S_k \ \in \sigma_i \}$$
実行可能なすべてのタスクの中で最高優先度タスクを$\tau_i$とすると，$\tau_i$はCPUに割り当てられます．
$S^*$を，現在$\tau_i$以外のタスクでロックされているセマフォの中で最高の優先度上限を持つセマフォとし，その優先度上限を $C(S^*)$とします．
セマフォ$S_k$で保護されたクリティカルセクションに入るためには，$C(S^*)$より高い優先度が必要です．
$P_i \leq C(S^*)$の場合，$S_k$上のロックが獲得できず，$S^*$上のロックを保持しているタスクによりセマフォ$S^*$上でブロックされます．
タスク$\tau_i$がセマフォ上でブロックされている時，そのセマフォを保持しているタスク$\tau_j$に優先度を送信します．
したがって，$\tau_j$は再開し，$\tau_i$の優先度でクリティカルセクションの残りの部分を実行します．
タスク$\tau_j$は$\tau_i$の優先度を継承（inherit）します．
一般的に，タスクはそのタスクによりブロックされたタスクの中で最高優先度を継承します．
$$p_j (R_k) = \underset{h}{\max} \{ P_j, \max \{ P_h | \tau_h {\rm \ is \ blocked \ on\ } R_k\} \} \tag{31.1}$$
$\tau_j$がクリティカルセクションを出ると，セマフォをアンロックし，そのセマフォでブロックされている最高優先度タスクがあれば，それが起床します．
他のタスクが$\tau_j$によりブロックされていない場合，$p_j$は通常優先度$P_j$に設定されます．
そうでなければ，式$(31.1)$より，$p_j$は$\tau_j$によりブロックされたタスクの中で最高優先度に設定されます．
優先度継承は推移的です．つまり，タスク$\tau_3$がタスク$\tau_2$をブロックし，タスク$\tau_2$がタスク$\tau_1$をブロックした場合，タスク $\tau_3$は$\tau_2$を介して$\tau_1$の優先度を継承します．

PCPのスケジュール例

PCPを説明するために，優先度の降順で整列している3つのタスク$\tau_1$，$\tau_2$，$\tau_3$を考えてみましょう．

最高優先度タスク$\tau_1$は，セマフォ$S_a$と$S_b$により保護された2つのクリティカルセクションに順次アクセスします．

タスク$\tau_2$はセマフォ$S_c$で保護されたクリティカルセクションのみにアクセスするのに対し，タスク$\tau_3$はセマフォ$S_c$を利用して$S_b$にネストしたアクセスを行います．

タスクの資源要件から，すべてのセマフォには以下の優先度上限が割り当てられます．

\begin{cases}
C(S_a) &=& P_1 \\
C(S_b) &=& P_1 \\
C(S_c) &=& P_2
\end{cases}

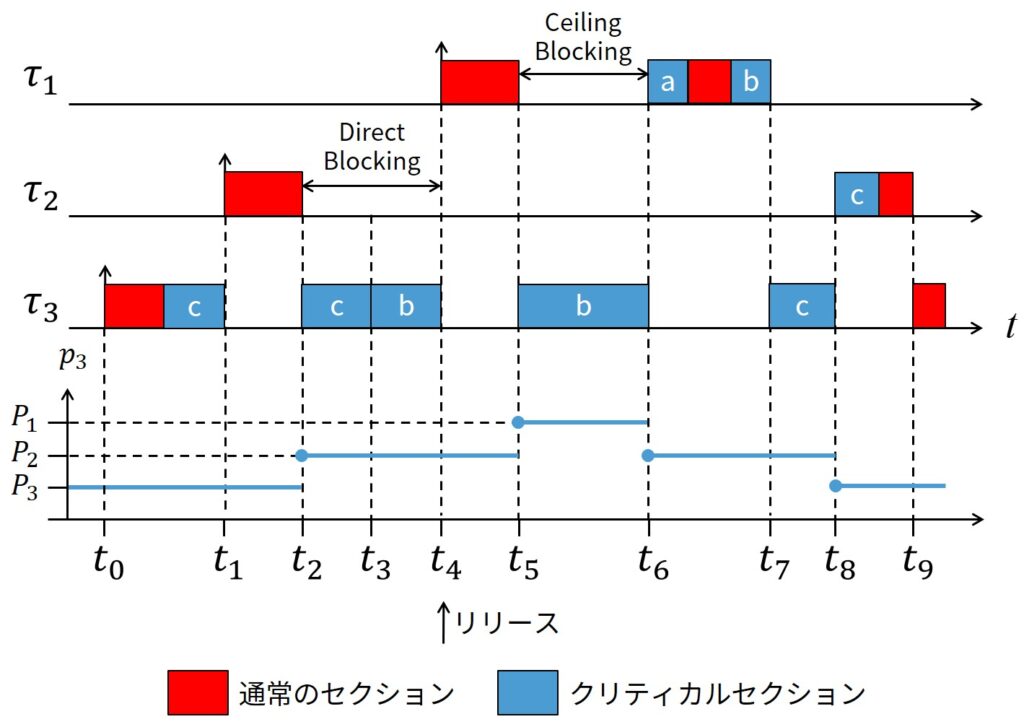
ここで，上図に示すようにイベントが発生するとします．

時刻$t_0$：$\tau_3$が起床し，唯一の実行可能（レディ）状態のタスクであるため，実行を開始し，後にセマフォ$S_c$をロックします．
時刻$t_1$：$\tau_2$は実行可能状態になり，$\tau_3$をプリエンプションします．
時刻$t_2$：$\tau_2$は$S_c$をロックしようとするが，$P_2$が$C(S_c)$より大きくないため，プロトコルによりブロックされます．
そして，$\tau_3$は$\tau_2$の優先度を継承して実行を再開します．
時刻$t_3$：$\tau_3$は$S_b$をロックすることで，ネストされたクリティカルセクションに正常に入りました．
他のタスクによりセマフォがロックされていないため，$\tau_3$は$S_b$をロックできることに注意してください．
時刻$t_4$：$\tau_3$が優先度$p_3=P_2$で実行している間，$P_1 > p_3$のため，$\tau_1$は実行可能状態になり$\tau_3$をプリエンプションします．
時刻$t_5$：$\tau_1$は，どのタスクにもロックされていない$S_a$をロックしようとします．
しかし，$\tau_1$は，他のタスクにより現在ロックされている全てのセマフォの中で最高の優先度上限$C (S_b)$より優先度が高くないため，プロトコルによりブロックされます．
$S_b$は$\tau_3$によりロックされているので，$\tau_3$は$\tau_1$の優先度を継承して実行を再開します．
時刻$t_6$：$\tau_3$はそのネストしているクリティカルセクションを出て，$S_b$のロックを解除します．
$\tau_1$が起床しているので，$\tau_3$は優先度$p_3=P_2$に戻ります．
この時点で，$P1 > C(S_c)$になります．
したがって，$\tau_1$は$\tau_3$をプリエンプションし，終了するまで実行します．
時刻$t_7$：$\tau_1$が終了し，$\tau_3$は優先度$p_3＝P_2$で実行を再開します．
時刻$t_8$：$\tau_3$は外側のクリティカルセクションを出て，$S_c$をアンロックします．
この時点で$\tau_2$は$\tau_3$をプリエンプションし，終了するまで実行します．
時刻$t_9$：$\tau_2$が終了したので，$\tau_3$は実行を再開します．

PCPは，PIPにより引き起こされるDirect BlockingとPush-Through Blockingに加えて，Ceiling Blockingと呼ばれる第3のブロッキングの形態を導入していることに注意してください．

Ceiling Blockingは，Chained Blockingやデッドロックを避けるために必要です．

先ほどの例では，タスク$\tau_1$によりCeiling Blockingが発生しています．

PCPの性質

ここでは，PCPの主な性質を紹介します．

これらは，スケジュール可能性解析や各々のタスクの最長ブロッキング時間の算出に利用されます．

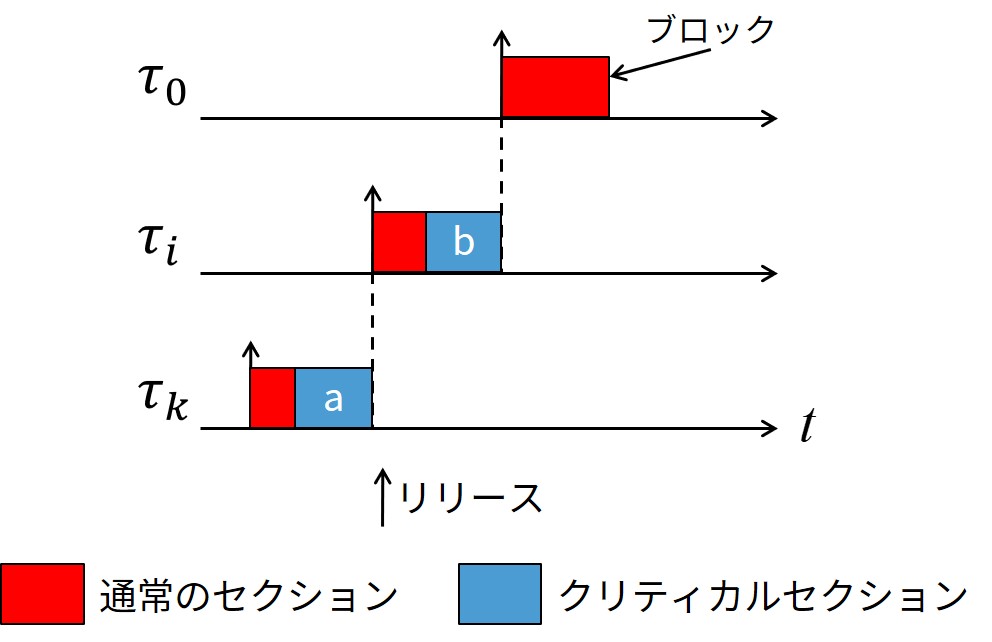
Absurd Situation that cannot Occur under PCP

補題31.1：あるタスク$\tau_k$がクリティカルセクション$Z_a$内で，クリティカルセクション$Z_b$に入ったタスク$\tau_i$によりプリエンプションされた場合，PCPの下では，$\tau_i$が終了するまで，$\tau_k$はタスク$\tau_i$の優先度以上の優先度を継承できない．

証明：$\tau_i$が終了する前に$\tau_k$がタスク$\tau_i$以上の優先度を継承する場合，$P_0 \geq P_i$のように$\tau_k$によりブロックされたタスク$\tau_0$が存在しなければなりません．

この状況を上図に示します．

しかし，これでは$\tau_k$により$\tau_0$がブロックされないという矛盾が生じてしまいます．

実際には，$\tau_i$はそのクリティカルセクションに入るので，その優先度は，すべての低優先度タスクにより現在ロックされているセマフォの最大上限$C^*$よりも高くなければなりませんので， $P_0 \geq P_i > C^*$になります．

しかし，$P_0 > C^*$なので，$\tau_0$は$\tau_k$によりブロックされません．

したがって，補題は証明されました．□

補題31.2：PCPは，推移ブロッキングを防止します．

証明：推移的なブロックが発生したとします．

つまり，優先度の降順に整列した3つのタスク$\tau_1$，$\tau_2$，$\tau_3$が存在し，$\tau_3$が$\tau_2$をブロック，$\tau_2$が$\tau_1$をブロックするとします．

プロトコルの推移性により，$\tau_3$は$\tau_1$の優先度を継承します．

しかし，このことは，$\tau_3$が$P_2$以上の優先度を継承できないことを示している補題31.1と矛盾します．

したがって，補題は証明されました．□

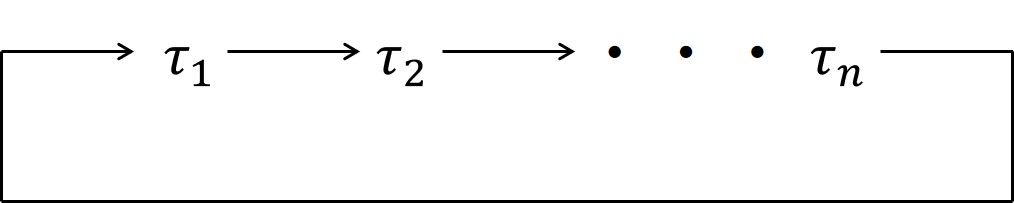
定理31.1：PCPはデッドロックを防ぐ．

証明：タスクは自分自身でデッドロックできないと仮定すると，上図に示すように，デッドロックはタスクが互いに待ち合うサイクルによってのみ形成されます．

しかし，このような状況では，プロトコルの推移性により，タスク$\tau_n$は，$P_n$より高いと仮定した$\tau_1$の優先度を継承します．

これは補題31.1と矛盾します．

したがって，定理は証明されました．□

定理31.2：PCPの下では，タスク$\tau_i$は，最長でも1つのクリティカルセクションの期間だけブロックできる．

証明：$\tau_i$が，$P_2 < P_1 < P_i$の2つの低優先度タスク$\tau_1$と$\tau_2$によりブロックされるとします．

$\tau_2$がそのブロックしているクリティカルセクションに最初に入るとし，$C_2^*$を$\tau_2$によりロックされたセマフォの中で最高の優先度上限とします．

この状況で，タスク$\tau_1$がクリティカルセクションに入る場合，$P_1 > C_2^*$が成立しなければなりません．

さらに，$\tau_i$は$\tau_2$によりブロックされると仮定したので，$P_i \leq C_2^*$が成立しなければなりません.

これは，$P_i \leq C_2^* \leq P_1$であることを意味し，$P_i > P_1$という仮定に矛盾します．

したがって，定理は証明されました．

PCPにおけるタスクのブロック時間の算出

各々のタスクの最長ブロッキング時間の評価は，定理31.2の結果に基づいて算出できます．

この定理によれば，あるタスク$\tau_i$は，$\tau_i$をブロックできるものの中で最長のクリティカルセクションの時間だけブロックされます．

タスク$\tau_i$をブロックできるクリティカルセクションの集合は，以下の補題からわかります．

補題31.3：PCPの下では，クリティカルセクション$z_{j,k}$（タスク$\tau_j$に属し，セマフォ$S_k$により保護されている）は，$P_j < P_i$で$C(S_k) \geq P_i$の場合に限り，タスク$\tau_i$をブロックできる．

証明：明らかに，もし$P_j \geq P_i$ならば，$\tau_i$は$\tau_j$をプリエンプションできず，したがって$z_{j,k}$上でブロックできません．

ここで，$P_j < P_i$，$C(S_k) < P_i$と仮定して，$\tau_i$が$z_{j,k}$でブロックされていると仮定します．

この仮定が矛盾につながることを示します．

実際，$\tau_i$が$\tau_j$にブロックされる場合，その優先度は$\tau_i$以外のタスクによりロックされているセマフォの中で最大の上限$C^*$以下でなければなりません．

したがって，$C(S_k) < P_i \leq C^*$となります．

一方，$C^*$は現在$\tau_i$以外のタスクによりロックされているセマフォの中で最大の上限であるので， $C^* \geq C(S_k)$ となり，矛盾します．

したがって，補題は証明されました．□

補題31.3の結果を用いて，タスク$\tau_i$は，資源の優先度上限が$P_i$以上の低優先度タスクに属するクリティカルセクションによってのみブロックされます．

$$\gamma_i = \{ Z_{j,k} \ | \ (P_j < P_i) {\rm \ and \ } (C(R_k) \geq P_i \} \tag{31.1}$$

そして，$\tau_i$は最大でも1回ブロックされるので，$\tau_i$が被る最長ブロック時間は，$\tau_i$をブロックできるものの中で最長のクリティカルセクションの持続時間になります．

$$B_i = \underset{j,k}{\max} \{ \delta_{j,k} - 1 \ | \ Z_{j,k} \in \gamma_i \} \tag{31.2}$$

タスク	$S_a (P_1)$	$S_b (P_1)$	$S_c (P_2)$
$\tau_1$	1	2	0
$\tau_2$	0	9	3
$\tau_3$	8	7	0
$\tau_4$	6	5	4

上表におけるPIPの例と同じ例を，簡単のために考えてみましょう．

式$(31.1)$によれば，次のようになります．

\begin{eqnarray}
\gamma_1 &=& \{ Z_{2b}, Z_{3a}, Z_{3b}, Z_{4a}, Z_{4b} \} \\
\gamma_2 &=& \{ Z_{3a}, Z_{3b}, Z_{4a}, Z_{4b}, Z_{4c} \} \\
\gamma_3 &=& \{ Z_{4a}, Z_{4b}, Z_{4c} \} \\
\gamma_4 &=& \{ \}
\end{eqnarray}

したがって，式$(31.2)$に基づいて，タスクのブロッキング係数は以下のように計算されます．

\begin{cases}
B_1 &=& \max(8, 7, 6, 5, 4) = 8 \\
B_2 &=& \max(7, 6, 5, 4, 3) = 7 \\
B_3 &=& \max(5, 4, 3) = 5 \\
B_4 &=& 0
\end{cases}

PCPの実装に関する考察

カーネルのデータ構造におけるPCPの主な貢献は，プロトコルによりブロックされたタスクをレディキューに保持できるので，セマフォキューがもはや必要ないということです．

特に，あるタスク$\tau_i$がセマフォ$S_k$上でプロトコルによりブロックされると，$S_k$を保持しているタスク$\tau_h$は$\tau_i$の優先度を継承してCPUに割り当てられ，$\tau_i$はレディキューに戻ります．

$\tau_h$が$S_k$をアンロックするとすぐに$p_h$が更新され，$p_h$が最初の実行可能状態のタスクの優先度よりも低くなると，コンテキストスイッチが実行されます．

PCPを実装するために，各々のセマフォ$S_k$は，$S_k$のロックを保持しているタスクのIDと$S_k$の上限を格納しなければなりません．

さらに，タスクのアクティブ優先度を格納するための追加フィールドをタスク制御ブロックに確保しなければなりません．

また，タスクがブロックされているセマフォのIDを格納するためのフィールドをタスク制御ブロックに持つことも便利です．

最後に，システムが現在ロックされているセマフォのリストを優先度の降順にすることで，プロトコルの実装を簡略化できます．

このリストは，あるタスクがクリティカルセクションに入るために乗り越えなければならない最大の優先度上限を算出したり，クリティカルセクションの終了時にタスクのアクティブ優先度を更新したりするのに便利です．

カーネルのデータ構造が上述のように拡張されている場合，PCPを実現するためのプリミティブpc_waitとpc_signalは，以下のように定義できます．

pc_wait(s)

実行中のタスク（$\tau_{exe}$）以外のタスクでロックされているセマフォの中から，最大の上限$C^*$を持つセマフォ$S^*$を探します．
$p_{exe} \leq C^*$の場合，$P_{exe}$を$S^*$を保持しているタスクに転送し，レディキューに$\tau_{exe}$を挿入し，最高優先度の実行可能状態のタスク（$\tau_{exe}$以外）を実行します．
$p_{exe} > C^*$の場合，または$s$がアンロックされている時はいつでも，セマフォ$s$をロックし，現在ロックされているセマフォのリストに$s$を追加し，$\tau_{exe}$を$s.holder$に格納します．

pc_signal(s)

現在ロックされているセマフォのリストから$s$を取り出します．
他のタスクが$\tau_{exe}$にブロックされていない場合は$p_{exe} = P_{exe}$とし，そうでない場合は$\tau_{exe}$にブロックされているタスクの中で最高優先度のものを$p_{exe}$とします．
レディタスクの中で最高優先度のものを$p^*$とします．
$p_{exe} < p^*$の場合，レディキューに$\tau_{exe}$を挿入し，レディタスク（$\tau_{exe}$以外）を最高優先度で実行します．

まとめ

今回はPriority Ceiling Protocol（PCP）を紹介しました．

具体的には，以下の内容を解説しました．

PCPの特徴
PCPの定義
PCPの性質
PCPにおけるタスクのブロック時間の算出
PCPの実装に関する考察

次回は，PCPを拡張する資源アクセスプロトコルを紹介します．

リアルタイムシステムで使われているリアルタイムOSは，主にC言語で書かれています．

私にC言語の無料相談をしたいあなたは，公式LINE「ChishiroのC言語」の友だち追加をお願い致します．

私のキャパシティもあり，一定数に達したら終了しますので，今すぐ追加しましょう！

: 元東大教員がおすすめするC言語を学べるオンラインプログラミングスクール5社

こういった悩みにお答えします．こういった私が解説していきます．私が大学の授業で初めてC言語を勉強した時は全然できませんでしたが，先生やTA，友人に相談しながら一生懸命C言語を勉強してできるようにな ...

続きを見る

次回はこちらからどうぞ．

: 【第32回】元東大教員から学ぶリアルタイムシステム「Stack Resource Policy」

こういった私から学べます．前回を読んでいない方はこちらからどうぞ．リアルタイムシステムの記事一覧はこちらからどうぞ． Stack Resource Policy（SRP） Stack Resour ...

続きを見る