【第30回】元東大教員から学ぶリアルタイムシステム「Priority Inheritance Protocol」

本記事の信頼性

リアルタイムシステムの研究歴12年．
東大教員の時に，英語でOS（Linuxカーネル）の授業．
2012年9月～2013年8月にアメリカのノースカロライナ大学チャペルヒル校（UNC）コンピュータサイエンス学部で客員研究員として勤務．C言語でリアルタイムLinuxの研究開発．
プログラミング歴15年以上，習得している言語: C/C++，Python，Solidity/Vyper，Java，Ruby，Go，Rust，D，HTML/CSS/JS/PHP，MATLAB，Assembler (x64，ARM)．
東大教員の時に，C++言語で開発した「LLVMコンパイラの拡張」，C言語で開発した独自のリアルタイムOS「Mcube Kernel」をGitHubにオープンソースとして公開．
2020年1月～現在はアメリカのノースカロライナ州チャペルヒルにあるGuarantee Happiness LLCのCTOとしてECサイト開発やWeb/SNSマーケティングの業務．2022年6月～現在はアメリカのノースカロライナ州チャペルヒルにあるJapanese Tar Heel, Inc.のCEO兼CTO．
最近は自然言語処理AIとイーサリアムに関する有益な情報発信に従事．

（AI全般を含む）自然言語処理AIの論文の日本語訳や，AIチャットボット（ChatGPT，Auto-GPT，Gemini（旧Bard）など）の記事を50本以上執筆．アメリカのサンフランシスコ（広義のシリコンバレー）の会社でプロンプトエンジニア・マネージャー・Quality Assurance（QA）の業務委託の経験あり．
（スマートコントラクトのプログラミングを含む）イーサリアムや仮想通貨全般の記事を200本以上執筆．イギリスのロンドンの会社で仮想通貨の英語の記事を日本語に翻訳する業務委託の経験あり．

こういった私から学べます．

前回を読んでいない方はこちらからどうぞ．

: 【第29回】元東大教員から学ぶリアルタイムシステム「資源アクセスプロトコルの例」

こういった私から学べます．前回を読んでいない方はこちらからどうぞ．リアルタイムシステムの記事一覧はこちらからどうぞ．資源アクセスプロトコルの例資源アクセスプロトコルの例として，以下の2つのシン ...

続きを見る

リアルタイムシステムの記事一覧はこちらからどうぞ．

: 元東大教員から学ぶリアルタイムシステム

こういった私から学べます．リアルタイムシステムとは，決められた時間（デッドライン）までに処理を完了しなければならない性質をもつシステムのことです．リアルタイムシステムは，ロボット，自動車や航空機な ...

続きを見る

リアルタイムシステムで使われているリアルタイムOSは，主にC言語で書かれています．

私にC言語の無料相談をしたいあなたは，公式LINE「ChishiroのC言語」の友だち追加をお願い致します．

私のキャパシティもあり，一定数に達したら終了しますので，今すぐ追加しましょう！

独学が難しいあなたは，元東大教員がおすすめするC言語を学べるオンラインプログラミングスクール5社で自分に合うスクールを見つけましょう．後悔はさせません！

: 元東大教員がおすすめするC言語を学べるオンラインプログラミングスクール5社

こういった悩みにお答えします．こういった私が解説していきます．私が大学の授業で初めてC言語を勉強した時は全然できませんでしたが，先生やTA，友人に相談しながら一生懸命C言語を勉強してできるようにな ...

続きを見る

Priority Inheritance Protocol（PIP）

Priority Inheritance Protocol（PIP）は，ブロックの原因となるタスクの優先度を変更することで，上限が無い優先度逆転を回避する資源アクセスプロトコルです．

具体的には，タスク$\tau_i$が1つ以上の高優先度タスクをブロックする時，一時的にブロックされたタスクの最優先度を引き継ぎます（inherit）．

これにより，中間優先度タスクが$\tau_i$をプリエンプションして，高優先度タスクがブロック時間を延長することを防ぎます．

Linuxでは，pthread_mutexattr_getprotocolでPTHREAD_PRIO_INHERITを設定するとPIPを利用できます．

PIPの定義

PIPの定義は，以下になります．

タスクは，アクティブ優先度に基づいてスケジュールされます．
同じ優先順位のタスクは，First-Come First-Served（FCFS）で実行されます．
タスク$\tau_i$がクリティカルセクション$z_{i,k}$に入ろうとし，資源$R_k$が低優先度タスク$\tau_j$に既に確保されている時，$\tau_i$はブロックされます．
そうでなければ，$\tau_i$はクリティカルセクション$z_{i,k}$に入ります．
タスク$\tau_i$があるセマフォ上でブロックされている時，そのセマフォを保持しているタスク$\tau_j$にそのアクティブ優先度を送信します．
したがって，$\tau_j$は，アクティブ優先度$p_j = p_i$でクリティカルセクションの残りの部分を再開して実行します．
タスク$\tau_j$は$\tau_i$の優先度を継承する（inherit）と言います．
一般的に，タスクはブロックするタスクの中の最高優先度タスクを継承します．
$$p_j (R_k) = \max \{ P_j, \underset{h}{\max} \{ P_h | \tau_h {\rm \ is \ blocked \ on \ } R_k \} \} \tag{30.1}$$
$\tau_j$がクリティカルセクションを出ると，セマフォのロックが解除され，そのセマフォ上でブロックされている最高優先度タスクがあれば，それが起床します．
さらに，$\tau_j$のアクティブ優先度は以下のように更新されます．
もし他のタスクが$\tau_j$によりブロックされていない場合，$p_j$はその通常優先度$P_j$に設定されます．
そうでなければ，式$(30.1)$により，$\tau_j$によりブロックされたタスクの中で最高優先度に設定されます．
優先度の継承は推移的（transitive）です．
すなわち，もしタスク$\tau_3$がタスク$\tau_2$をブロックし，タスク$\tau_2$がタスク$\tau_1$をブロックする場合，タスク$\tau_3$は$\tau_2$を介して$\tau_1$の優先度を継承します．

PIPのスケジュール例

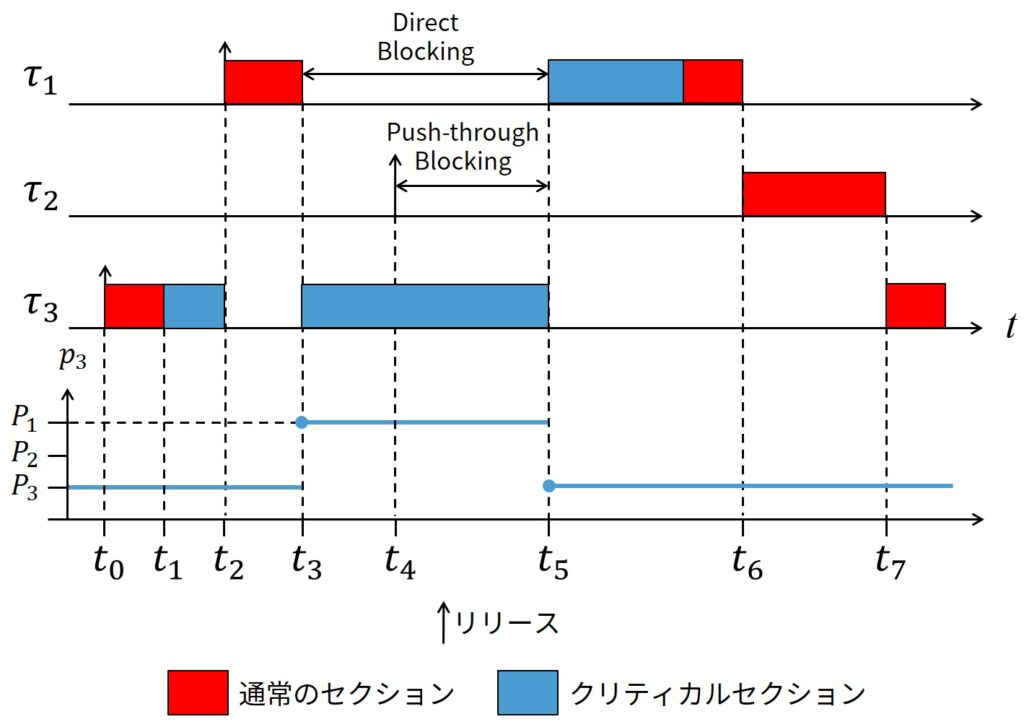
まず，第28回リアルタイムシステムの4番目の図と同じ状況を考え，優先度逆転現象が優先度継承プロトコルによってどのように制限されるのかを示します．

上図に修正されたスケジュールを示します．

時刻$t_3$までは優先度継承が発生しないため，スケジュールの変動はありません．

時刻$t_3$では，$\tau_1$は$\tau_3$にブロックされるので，$\tau_3$は$\tau_1$の優先度を継承し，そのクリティカルセクションの残りの部分($t_3$から$t_5$まで)を最高優先度で実行します．

この状態では，時刻$t_4$では，$\tau_2$は$\tau_3$をプリエンプションできず，$\tau_1$を干渉しません（優先度逆転現象の制限）．

$\tau_3$がそのクリティカルセクションを出ると，$\tau_1$が起床し，$\tau_3$は通常優先度に戻ります．

時刻$t_5$では，CPUは実行可能な最高優先度タスクである$\tau_1$を実行し，$\tau_2$は$\tau_1$が終了した時刻$t_6$にのみ実行開始できます．

上図の一番下のタイムラインに，時間関数としての$\tau_3$のアクティブ優先度も示します．

この例から，高優先度タスクでは以下の2種類のブロッキングが発生することがわかります．

Direct Blocking：高優先度タスクが，低優先度タスクが既に保持している資源を獲得しようとした時に発生します．共有資源の一貫性を確保するためには，Direct Blockingが必要です．
Push-Through Blocking：中間優先度のタスクが，直接ブロックするタスクより高優先度を継承した低優先度タスクによってブロックされる場合に発生します．制限がない優先度逆転を回避するために必要です．

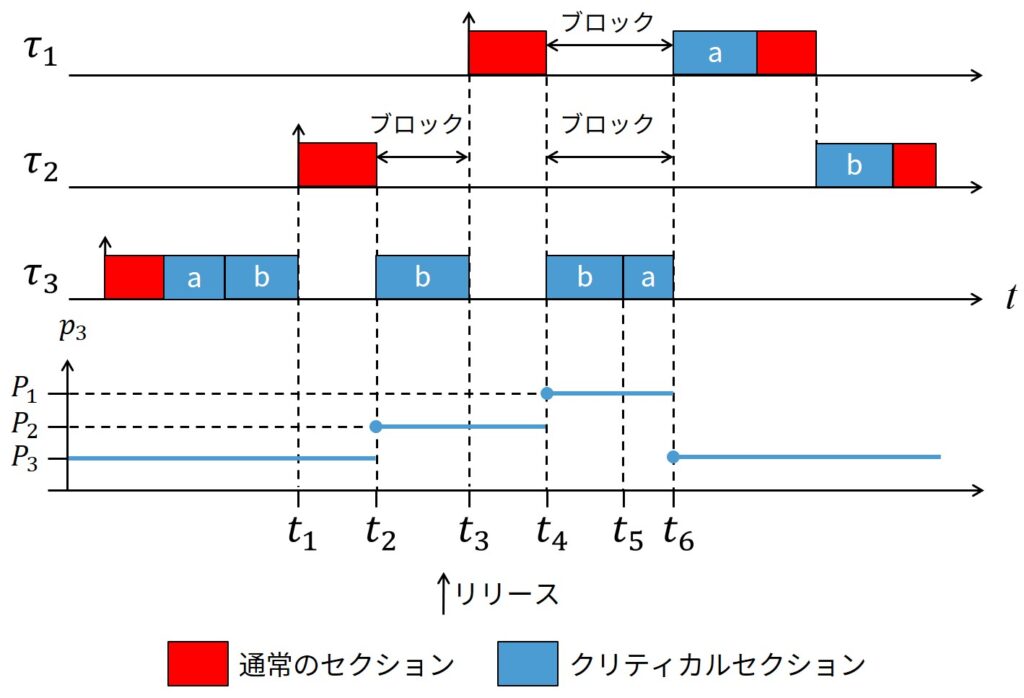
Priority Inheritance with Nested Critical Sections

ほとんどの場合，タスクがクリティカルセクションを出た時には，そのタスクが入ったときの優先度に戻ることに注意してください．

しかし，これは必ずしも正しいとは限りません．

上図の例を考えてみましょう．

ここでは，タスク$\tau_1$はセマフォ$S_a$で保護された資源$R_a$を利用し，タスク$\tau_2$はセマフォ$S_b$で保護された資源$R_b$を利用し，タスク$\tau_3$はネスト（入れ子）された方法で両方の資源を利用します（$S_a$が最初にロックされます）．

時刻$t_1$では，$\tau_2$はネストしているクリティカルセクション内でプリエンプションされます．

したがって，時刻$t_2$において，$\tau_2$が$S_b$をロックしようとすると，$\tau_3$はその優先度$P_2$を継承します．

同様に，時刻$t_3$では，$\tau_1$が同じクリティカルセクション内で$\tau_3$をプリエンプションします．

時刻$t_4$では，$\tau_1$が$S_a$をロックする時，$\tau_3$が優先度$P_1$を継承します．

時刻$t_5$では，$\tau_3$がセマフォ$S_b$をアンロックする時，タスク$\tau_2$は起床するが，$\tau_3$はブロックされたままです．

したがって，$\tau_3$は$\tau_1$の優先度で実行を継続します．

時刻$t_6$では，$\tau_3$は$S_a$をアンロックします．

他のタスクはブロックされていないので，$\tau_3$は通常優先度$P_3$に戻ります．

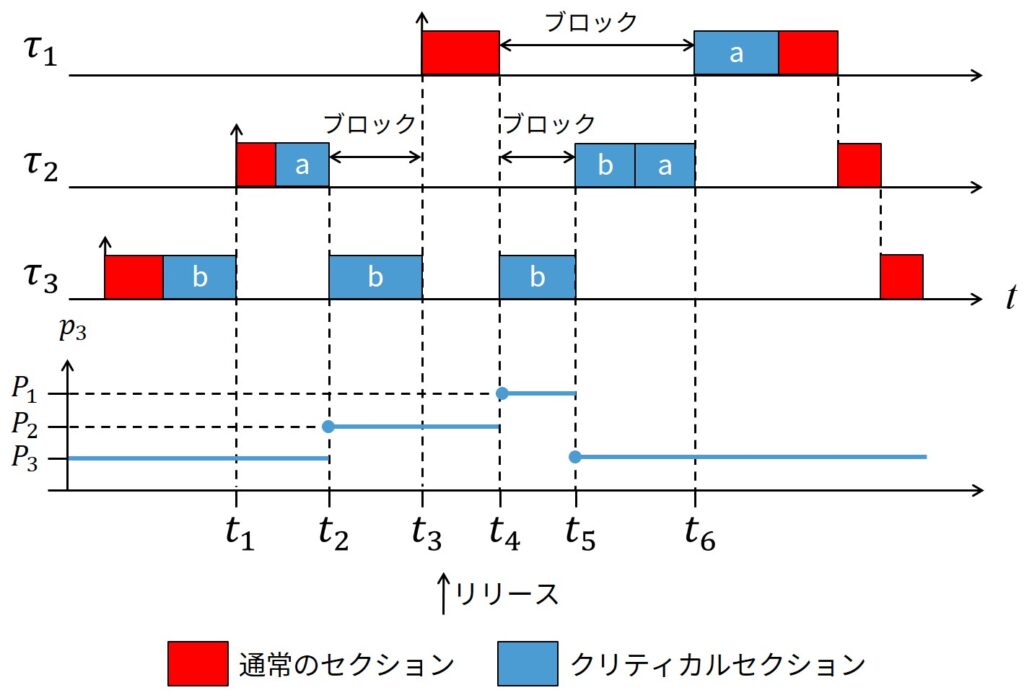
Example of Transitive Priority Inheritance

上図に推移的な優先度継承の例を示します．

ここで，タスク$\tau_1$はセマフォ$S_a$で保護された資源$R_a$を利用し，タスク$\tau_3$はセマフォ$S_b$で保護された資源$R_b$を利用し，タスク$\tau_2$はネストされた方法で両方の資源を利用します．（$S_a$は外部のクリティカルセクションを保護し，$S_b$は内部のクリティカルセクションを保護します．）

時刻$t_1$では，$\tau_3$はそのクリティカルセクション内で$\tau_2$にプリエンプションされ，それに続いて最初のクリティカルセクション（$S_a$により保護されたもの）に入り，時刻$t_2$ではセマフォ$S_b$上でブロックされます．

結果として，$\tau_3$は優先度$P_2$を継承して実行を再開します．

時刻$t_3$では，$\tau_3$は，時刻$t_4$で資源$R_a$を獲得しようとする$\tau_1$によりプリエンプションされます．

$S_a$は$\tau_2$によりロックされているので，$\tau_2$は$P_1$を継承します．

しかし，$\tau_2$は$\tau_3$にブロックされます．

したがって，推移性のために，$\tau_3$は$\tau_2$を介して優先度$P_1$を継承します．

$\tau_3$がクリティカルセクションを出ると，他のタスクはブロックされません．

したがって，$\tau_3$は通常優先度$P_3$で実行を再開します．

優先度$P_1$は$\tau_2$に継承され，時刻$t_6$まで$\tau_1$をブロックしたままになります．

PIPの性質

PIPの主な性質を紹介します．

これらの性質を利用して，周期タスクセットのスケジュール可能性を解析し，各タスクの最長ブロッキング時間を算出します．

補題30.1：セマフォ$S_k$は，$S_k$が$P_i$より低優先度タスクと$P_i$より高優先度のタスクの両方からアクセスされた場合に限り，タスク$\tau_i$へのPush-Through Blockingを引き起こす．

証明：セマフォ$S_k$は$P_i$より低優先度タスク$\tau_l$からアクセスされるが，$P_i$より高優先度タスクからはアクセスされないとします．

そして，$\tau_l$は$P_i$より高優先度を継承することはできませんので，$\tau_l$は$\tau_i$にプリエンプションされます．

したがって，補題は証明されました．□

補題30.2：推移的な優先度継承は，ネストされたクリティカルセクション内でのみ発生する．

証明：高優先度タスク$\tau_H$が優先度の中間優先度タスク$\tau_M$にブロックされ，さらに低優先度タスク$\tau_L$にブロックされた場合，推移的な優先度継承が発生します（上図参照）．

$\tau_H$は$\tau_M$によりブロックされるので，$\tau_M$はセマフォ$S_a$を保持しなければなりません．

しかし，$\tau_M$は他のセマフォ$S_b$上の$\tau_L$にもブロックされています．

これは，$\tau_M$が$S_a$に保護されたクリティカルセクション内で$S_b$をロックしようとしたことを意味しています．

したがって，補題は証明されました．□

補題30.3：もし$\tau_i$をブロックできる$l_i$個の低優先度タスクがある場合，$\tau_i$が利用するセマフォの数に関係なく，最大でも$l_i$クリティカルセクション（$l_i$個の低優先度タスク毎に1つずつ）の間，$\tau_i$をブロックできる．

証明：タスク$\tau_i$はが低優先度タスク$\tau_j$にブロックされる場合は，$\tau_j$が$\tau_i$をブロックできるクリティカルセクション$z_{j,k}$内でプリエンプションされる場合のみです．

一旦$\tau_j$が$z_{j,k}$を出ると，$\tau_i$にプリエンプションされます．

したがって，$\tau_i$は再び$\tau_j$にブロックされません．

同じ状況が，$l_i$個の低優先度タスク毎に発生する可能性があります．

したがって，$\tau_i$はほとんどの場合，$l_i$回ブロックされます．□

補題30.4：タスク$\tau_i$をブロックできる$s_i$個の異なるセマフォが存在する場合，$\tau_i$が利用するクリティカルセクションの数に関係なく，最大で$s_i$個のセマフォごとに1つのクリティカルセクションの間，$\tau_i$をブロックできる．

証明：セマフォはこの場合バイナリセマフォ（同時に1つのタスクのみクリティカルセクションに入ることが可能）なので，低優先度タスクの1つ$\tau_j$だけが，特定のセマフォ$S_k$に対応するクリティカルセクション内に入れます．

$S_k$がアンロックされると，$\tau_j$はプリエンプションされ，もはや$\tau_i$をブロックできません．

$\tau_i$をブロックできるすべての$s_i$個のセマフォが$s_i$個の低優先度タスクによりロックされるならば，$\tau_i$は最大で$s_i$回ブロックされます．□

定理30.1：Priority Inheritance Protocolの下では，タスク$\tau_i$は最大でも$\alpha_i = \min(l_i, s_i)$ クリティカルセクションの持続時間だけブロックされます．ここで，$l_i$は$\tau_i$をブロックできる低優先度タスクの数であり，$s_i$は$\tau_i$をブロックできる別個のセマフォの数である．

証明：補題30.3と補題30.4から自明です．□

PIPにおけるタスクのブロック時間の算出

各々のタスクの最長ブロッキング時間の評価は，定理30.1の結果に基づいて算出できます．

しかし，ブロッキング係数$B_i$の正確な評価は，低優先度タスクの各々の重要なセクションが，Direct Blocking，Push-Through Blocking，または推移的な優先度継承を介して$\tau_i$と干渉する可能性があるため，非常に複雑です．

そこで，ネストされたクリティカルセクションを利用しないタスクのブロッキング係数を算出するために利用できる単純化されたアルゴリズムを紹介します．

この場合，実際に補題30.2は，推移的な優先度継承が起こらないことを保証しているので，すべての可能なブロッキング条件の解析は単純化されます．

第28回で紹介した用語を使用して，推移的なブロッキングがない場合，タスク$\tau_i$をブロッキングできるクリティカルセクションの集合$\gamma_i$は，以下のように算出できます．

低優先度タスク$\tau_j$が共有する$\tau_i$へのDirect Blockingを引き起こすセマフォのセットは以下になります．
$$\sigma_{i,j}^{\rm dir} = \sigma_i \cap \sigma_j$$
低優先度タスク$\tau_j$が共有する$\tau_i$へのPush-Through Blockingを引き起こすセマフォの集合は以下になります．
$$\sigma_{i,j}^{\rm pt} = \underset{h: P_h > P_i}{\bigcup} \sigma_h \cap \sigma_j$$
低優先度タスク$\tau_j$が共有する$\tau_i$を（Direct BlockingまたはPush-Through Blockingで）ブロックできるセマフォの集合は以下になります．
$$\sigma_{i,j} = \sigma_{i,j}^{\rm dir} \cup \sigma_{i,j}^{\rm pt} = \underset{h: P_h \geq P_i}{\bigcup} \sigma_h \cap \sigma_j$$
$\tau_j$が利用する最長クリティカルセクションの集合で，（Direct BlockingまたはPush-Through Blockingで）$\tau_i$をブロックできるものは以下になります．
$$\gamma_{i,j} = \{ Z_{j,k} | (P_j < P_i) {\rm \ and \ } ( R_k \in \sigma_{i,j} \}$$
$\tau_i$を（Direct BlockingまたはPush-Through Blockingで）ブロックできるすべてのクリティカルセクションの集合は以下になります．
$$\gamma_i = \underset{j: P_j < P_i}{\bigcup} \gamma_{i,j}$$
$B_i$は，$\gamma_i$内の$\alpha_i$個のクリティカルセクションの長さの最大和になります．
$\tau_i$は同じタスクや同じセマフォにより二度ブロックされないので，異なるタスクや異なるセマフォを参照する項$\delta_{j,k}$だけを合計は含むべきであることに注意してください．

残念ながら，ネストされた資源を考慮しなくても，各々のブロッキング係数の正確な算出には，すべての可能な$\alpha_i$の持続時間の中から最大の合計を見つけるための組み合わせ探索が必要です．

しかし，より単純な上限値は，以下のアルゴリズムで算出できます．

補題30.3より，タスク$\tau_i$は$l_i$個の低優先度タスクごとに最大1回ブロックできます．
したがって，$\tau_i$をブロックできる各々の低優先度タスク$\tau_j$について，$\tau_i$をブロックできるタスクの中で最長クリティカルセクションの持続時間を合計します．
この合計$B_i^l$は以下になります．
$$B_i^l = \sum_{j: P_j < P_i} \underset{k}{\max} \{ \delta_{j,k} - 1\ |\ Z_{j,k} \in \gamma_i \}$$
補題30.4より，タスク$\tau_i$をブロックできる$s_i$個のセマフォのそれぞれについて，最大1回タスク$\tau_i$ をブロックできます．
したがって，$\tau_i$をブロックできる各々のセマフォ$S_k$について，$\tau_i$をブロックできるセマフォの中で最長クリティカルセクションの持続時間を合計します．
この合計$B_i^s$は以下になります．
$$B_i^s = \sum_{k=1}^m \underset{j}{\max} \{ \delta_{j,k} - 1 \ | \ Z_{j,k} \in \gamma_i \}$$
定理30.1より，最大でも$\alpha_i = \min(l_i, s_i)$のクリティカルセクションの持続時間だけ，$\tau_i$をブロックできます．
したがって，$B_i^l$と$B_i^s$の間の最小値として$B_i$を算出します．
$$B_i = \min(B_i^l, B_i^s)$$

各々のセマフォ$S_k$に対して，$S_k$を利用するタスクの中で最高優先度タスクに等しい上限$C(S_k)$を定義すれば，タスクをブロックできるクリティカルセクションの特定は非常に単純化されます．

$$C (S_k) \overset{\rm def}{=} \underset{i}{\max} \{ P_i \ | \ S_k \in \sigma_i \}$$

そうすると，次の補題が成立します．

補題30.5：ネストされたクリティカルセクションがない場合，$S_k$により保護された$\tau_j$のクリティカルセクション$z_{j,k}$は，$P_j < P_i \leq C(S_k)$ の場合に限り，$\tau_i$をブロックできます．

証明：$P_i \leq P_j$の場合，タスク$\tau_i$は$\tau_j$をプリエンプションできません．

そのため，$\tau_j$により直接ブロックされることはありません．

一方，$C(S_k) < P_i$の場合，$C(S_k)$の定義より，$S_k$を利用するタスクは，$P_i$より高い優先度を持てません．

したがって，補題30.1から，$z_{j,k}$は$\tau_i$にPush-Through Blockingを起こせません．

最後に，ネストされたクリティカルセクションが存在しないので，補題30.2は$z_{j,k}$が推移的なブロッキングを引き起こさないことを保証しています．

補題は証明されました．□

補題30.5の結果を利用して，ブロッキング項$B_i^l$と$B_i^s$を以下のように決定できます．

\begin{eqnarray}
B_i^l &=& \sum_{j=i+1}^n \underset{k}{\max} \{ \delta_{j,k} - 1\ | \ C(S_k) \geq P_i \} \\
B_i^s &=& \sum_{k=1}^m \underset{j>i}{\max} \{ \delta_{j,k} - 1 \ | \ C(S_k) \geq P_i \}
\end{eqnarray}

Algorithm: Blocking Time Computation
Input: durations $\delta_{i,k}$ for each task $\tau_i$ and each semaphore $S_k$
Output: $B_i$ for each task $\tau_i$
// Assumes tasks are ordered by decreasing priorities
(1) begin
(2) for i := 1 to n - 1 do // for each task
(3) $B_i^l$ := 0;
(4) for j := i + 1 to n do // for each lower priority task
(5) $D_{max}$ := 0;
(6) for k := 1 to m do // for each semaphore
(7) if ($C(S_k) \geq P_i$) and ($\delta_{j,k} > D_{max}$) do
(8) $D_{max}$ := $\delta_{j,k}$;
(9) end
(10) end
(11) $B_i^l$ := $B_i^l$ + $D_{max}$ - 1;
(12) end
(13) $B_i^s$ := 0;
(14) for k := 1 to m do // for each semaphore
(15) $D_{max}$ := 0;
(16) for j := i + 1 to n do // for each lower priority task
(17) if ($C(S_k) \geq P_i$) and ($\delta_{j,k} > D_{max}$) do
(18) $D_{max}$ := $\delta_{j,k}$;
(19) end
(20) end
(21) $B_i^s$ := $B_i^s$ + $D_{max}$ - 1;
(22) end
(23) $B_i$ := min($B_i^l$, $B_i^s$);
(24) end
(25) $B_n$ := 0;
(26) end

上記のアルゴリズムによりブロッキング時間を算出します．

このアルゴリズムは，タスクセットが，$m$個の異なるバイナリセマフォを利用する$n$個の周期タスクで構成されていることを想定します．

タスクは，すべての$i < j$に対して$P_i > P_j$となるように，優先度の低い順に並べられます．

クリティカルセクションはネストになっていません．

ブロッキング係数$B_n$は常に0であることに注意してください．

アルゴリズムの計算量は$\mathcal{O}(mn^2)$です．

このアルゴリズムによって導出されたブロッキング係数はタイトではない（悲観的な）ことに注意してください．

実際には，$B_i^l$は同じセマフォにより保護された2つ以上のクリティカルセクションを考慮することで算出できるかもしれませんが，補題30.4により2個以上のクリティカルセクションの最大でも1個だけしか$\tau_i$をブロックできません．

同様に，$B_i^s$は同じセマフォにより保護された2つ以上のクリティカルセクションを考慮することで算出できるかもしれませんが，補題30.3により2個以上のクリティカルセクションの最大でも1個だけしか$\tau_i$をブロックできません．

しかし，これらのケースを除外するには，クリティカルセクションのすべての可能な組み合わせの中から最大ブロッキング時間を算出しなければならないため，計算量は指数関数的に増大します．

Rajkumarにより提案された網羅的探索に基づくアルゴリズムは，上記のアルゴリズムより優れた最大ブロッキング時間を見つけられますが，指数関数的な複雑さを持っています．

ブロッキング時間の算出例

タスク	$S_a (P_1)$	$S_b (P_1)$	$S_c (P_2)$
$\tau_1$	1	2	0
$\tau_2$	0	9	3
$\tau_3$	8	7	0
$\tau_4$	6	5	4

上記のアルゴリズムを説明するために，4つのタスクが3つのセマフォを共有している上表の例を考えてみましょう．

各々のタスク$\tau_i$について，同じセマフォ$S_k$を利用しているタスクの中で最長クリティカルセクションの持続時間を$\delta_{i,k}$で表します．

$\delta_{i,k} = 0$は，タスク$\tau_i$がセマフォ$S_k$を利用しないことを意味します．

セマフォの最高優先度は（）内に記載します．

上記のアルゴリズムによると，タスクのブロッキング係数は以下のように計算されます（各々の持続時間から1ユニット時間が差し引かれることに注意してください）．

\begin{eqnarray}
B_1^l &=& 8 + 7 + 5 = 20 \\
B_1^s &=& 7 + 8 = 15 \ \ \ \ \ \ \ \ \ \ ==> B_1 = 15 \\
\\
B_2^l &=& 7 + 5 = 12 \\
B_2^s &=& 7 + 6 + 3 = 16 \ \ \ ==> B_2 = 12 \\
\\
B_3^l &=& 5 \\
B_3^s &=& 5 + 4 + 3 = 12 \ \ \ ==> B_3 = 5 \\
\\
B_4^l &=& B_4^s = 0 \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ ==> B_4 = 0 \\
\end{eqnarray}

なぜアルゴリズムが悲観的なのかを理解するために，セマフォ$S_1$により保護された2つのクリティカルセクションの持続時間を加算することで$B_2^l$が算出されることに注意してください．（実際には発生しません．）

PIPの実装に関する考察

PIPの実装には，タスクやセマフォに関連するカーネルのデータ構造を少し変更する必要があります．

まず第一に，各々のタスクは通常優先度とアクティブ優先度を持っていなければならず，これらはタスク制御ブロック（TCB：Task Control Block）に格納する必要があります．

また，継承機構を高速化するために，各々のセマフォがロックを保持しているタスクを追跡すると便利です．

この追跡は，セマフォのデータ構造の中に，保持しているタスクIDを格納するための特定のフィールド（例：holder）を追加することで実現できます．

このようにすれば，セマフォ上でブロックされているタスクは，優先度を送信するためにロックを保持しているタスクをすぐに特定できます．

同様に，各々のタスクがブロックされたセマフォを追跡すれば，推移的継承は単純化されます．

この場合，この情報は，TCBのフィールド（例：lock）に格納されなければなりません．

カーネルのデータ構造が上述のように拡張されていると仮定すると，PIPを実現するためのプリミティブpi_waitとpi_signalは，以下のように定義できます．

pi_wait(s)

セマフォ$s$が空いている場合はロックされ，実行タスクの名前がセマフォデータ構造体のholderフィールドに格納されます．
セマフォ$s$がロックされている場合，実行タスクは$s$セマフォキューにブロックされ，セマフォIDはTCBのlockフィールドに格納され，その優先度は以下の通りです．
そのようなタスクが他のセマフォ上でブロックされている場合には，そのような推移ルールが適用されます．
そして，最高優先度の実行可能状態のタスクがCPUに割り当てられます．

pi_signal(s)

セマフォ$s$のキューが空であれば (つまり$s$上にタスクがブロックされていなければ)，$s$はアンロックされます．
セマフォ$s$のキューが空でなければ，キュー内の最高優先度タスクが起床し，そのIDはs.holderに格納され，実行中のタスクのアクティブ優先度が更新され，最高優先度の実行可能状態のタスクがCPUに割り当てられます．

PIPの未解決の問題

PIPは優先度逆転現象を制限していますが，ブロッキングの連鎖を形成できるため，タスクのブロッキング期間はまだ相当なものになる可能性があります．

もう一つの問題は，プロトコルがデッドロックを防止していないことです．

Chained Blocking

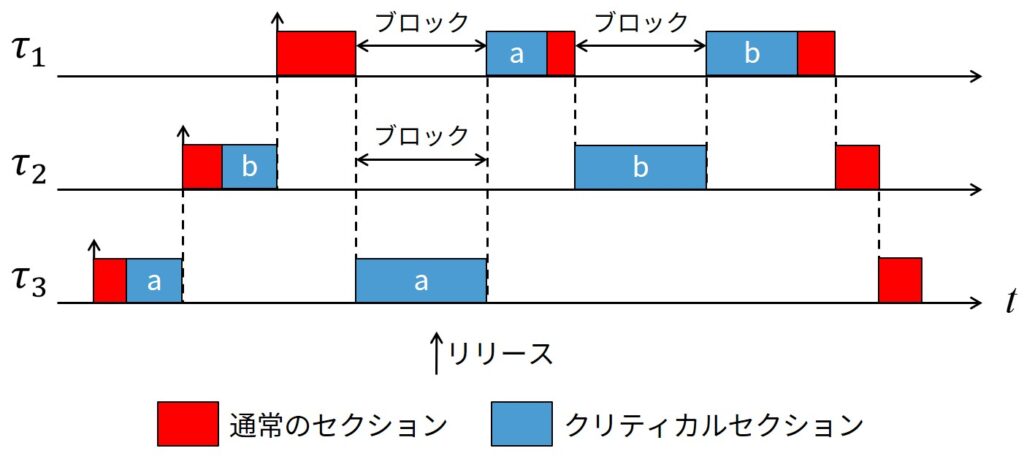
2つのセマフォ$S_a$と$S_b$を共有する優先度の降順に並べられた3つのタスク$\tau_1$，$\tau_2$，$\tau_3$を考えてみましょう．

$\tau_1$が$S_a$と$S_b$に順次アクセスし，$\tau_2$が$S_b$にアクセスし，$\tau_3$が$S_a$にアクセスするとします．

また，$\tau_3$は$S_a$をロックし，そのクリティカルセクション内で$\tau_2$によりプリエンプションされるとします．

同様に，$\tau_2$は$S_b$をロックし，そのクリティカルセクション内では$\tau_1$によりプリエンプションされます．

その例を上図に示します．

この状況では，その資源を利用しようとすると，$\tau_1$は2回のクリティカルセクションの間（1回目は$\tau_3$が$S_a$を解放するのを待つ，2回目は$\tau_2$が$S_b$を解放するのを待つ）ブロックされます．

これをChain Blockingと言います．

最悪の場合，$\tau_1$が低優先度の$n$個のタスクによりロックされた$n$個の異なるセマフォにアクセスした場合，$\tau_1$は$n$個のクリティカルセクションの間ブロックされます．

デッドロック

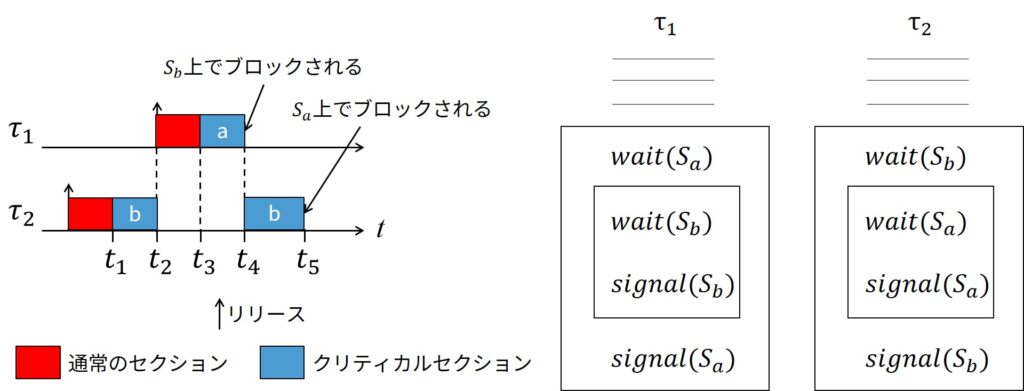
上図に示すように，2つのセマフォを入れ子にして逆順に利用する2つのタスクを考えてみましょう．

ここで，時刻$t_1$で，$\tau_2$がセマフォ$S_b$をロックし，そのクリティカルセクションに入ったとします．

時刻$t_2$において，$\tau_1$は$S_a$をロックする前に$\tau_2$をプリエンプションします．

時刻$t_3$で，$\tau_1$は空いている$S_a$をロックし，その後，時刻$t_4$で$S_b$にブロックされます．

このとき，$\tau_2$は$\tau_1$の優先度で実行を再開し，継続します．

優先度継承は，時刻$t_5$で$\tau_2$が$S_a$をロックしようとしたときに発生するデッドロックを防げません．

しかし，デッドロックはPIPに依存しているのではなく，セマフォの誤った利用によって引き起こされることに注意してください．

この場合，デッドロック問題は，セマフォアクセスに全体的な順序付けを課すことで解決できます．

まとめ

今回はPriority Inheritance Protocol（PIP）を紹介しました．

具体的には，以下の内容を解説しました．

PIPの特徴
PIPの定義
PIPの性質
PIPにおけるタスクのブロック時間の算出
PIPの実装に関する考察
PIPの未解決の問題

次回は，PIPの未解決の問題を解決する資源アクセスプロトコルを紹介します．

リアルタイムシステムで使われているリアルタイムOSは，主にC言語で書かれています．

私にC言語の無料相談をしたいあなたは，公式LINE「ChishiroのC言語」の友だち追加をお願い致します．

私のキャパシティもあり，一定数に達したら終了しますので，今すぐ追加しましょう！

: 元東大教員がおすすめするC言語を学べるオンラインプログラミングスクール5社

こういった悩みにお答えします．こういった私が解説していきます．私が大学の授業で初めてC言語を勉強した時は全然できませんでしたが，先生やTA，友人に相談しながら一生懸命C言語を勉強してできるようにな ...

続きを見る

次回はこちらからどうぞ．

: 【第31回】元東大教員から学ぶリアルタイムシステム「Priority Ceiling Protocol」

こういった私から学べます．前回を読んでいない方はこちらからどうぞ．リアルタイムシステムの記事一覧はこちらからどうぞ． Priority Ceiling Protocol（PCP） Priority ...

続きを見る