【第26回】元東大教員から学ぶリアルタイムシステム「Constant Bandwidth Server」

こういった私から学べます．

前回を読んでいない方はこちらからどうぞ．

リアルタイムシステムの記事一覧はこちらからどうぞ．

リアルタイムシステムで使われているリアルタイムOSは，主にC言語で書かれています．

私にC言語の無料相談をしたいあなたは，公式LINE「ChishiroのC言語」の友だち追加をお願い致します．

私のキャパシティもあり，一定数に達したら終了しますので，今すぐ追加しましょう！

独学が難しいあなたは，元東大教員がおすすめするC言語を学べるオンラインプログラミングスクール5社で自分に合うスクールを見つけましょう．後悔はさせません！

Constant Bandwidth Server（CBS）

Constant Bandwidth Server（CBS）はバンド幅の予約を効果的に実装する機構です．

また，CBSはLinuxのリアルタイムスケジューリングポリシー「SCHED_DEADLINE」を実装するためにEDFと一緒に利用される技術です．

SCHED_DEADLINEを含むLinuxカーネルのプロセススケジューリングを知りたいあなたはこちらからどうぞ．

DSSのように，もし\(U_s\)が非周期サーバの割り当てるCPU利用率（バンド幅）の場合，その合計CPU利用率は過負荷の場合でも\(U_s\)を超えませんが，この性質はTBSでは有効ではありません．

TBSのCPU利用率が\(U_s\)に制限される状況は，全ての非周期タスクのジョブが予想される最悪実行時間を超えない場合のみです．

CBSはDSSより短い性能を発揮し，TBSが達成可能な性能に匹敵するレベルです．

CBSの基本的なアイデアを以下に説明します．

新しいジョブがシステムに到着した時，そのジョブは（予約されたバンド幅内での要求を満たすために）適切な絶対デッドラインを割り当られ，EDFのレディーキューに挿入されます．

もしジョブが予想より多く実行しようとした場合，他のタスクへの干渉を減らすために，その絶対デッドラインは延期されます（優先度が低下します）．

絶対デッドラインを延期することにより，タスクは実行する資格を保持することに注意して下さい．

この方法では，CBSは仕事量を保つ（Work Conserving）アルゴリズムとして振る舞い，効果的な方法で利用可能なスラックを最大限利用します．

したがって，仕事量を保たない（Non-Work Conserving）アルゴリズムや他の予約する手法（例：バックグラウンドでジョブの余分な部分をスケジュール）と比較して，より良い応答性を提供します．

もしタスクのサブセットが一つのサーバで扱われる場合，サブセット内にある全てのタスクは同じバンド幅を共有しますので，タスク間でアイソレーション（分離して独立で実行すること）しません．

それにもかかわらず，システム内にある全ての他のタスクは，サブセット内で発生するオーバーランに対して保護されます．

あらゆるハードデッドラインをミスしないためには，非周期サーバに採用されるデッドライン割り当てルールを注意深く設計しなければなりません．

次の章では，CBSを正確に定義し，あらゆる非周期タスクの実行や到着パターンに対しての正しさを形式的に証明します．

CBSの定義

CBSの定義は以下になります．

• CBSはバジェット（非周期サーバの容量）\(c_s\)と順序対\((Q_s, T_s)\)により特徴づけられます．\(Q_s\)は最大バジェット，\(T_s\)は非周期サーバの周期です．非周期サーバのバンド幅は\(U_s=Q_s/T_s\)になります．
  各々の時刻で，固定された絶対デッドライン\(d_{s,k}\)は非周期サーバに関連します．絶対デッドラインの初期値は\(d_{s,0}\)になります．
• 各々の非周期サーバのジョブ\(J_{i,j}\)は，現在の非周期サーバの絶対デッドライン\(d_{s,k}\)と同じ動的な絶対デッドライン\(d_{i,j}\)を割り当てられます．
• 非周期サーバのジョブが実行する時はいつでも，バジェット\(c_s\)は同じ量が減ります．
• \(c_s=0\)の時，非周期サーバのバジェットは最大値\(Q_s\)に再充填され，新しい非周期サーバの絶対デッドラインは\(d_{s,k+1} = d_{s,k} + T_s\)に設定されます．
  バジェットが0になる有限区間がないことに注意して下さい．
• もし待機状態のジョブがある場合（すなわち，もし実行されるジョブ\(J_{i,j}\)が\(r_{i,j} \leq t \leq f_{i,j}\)を満たす場合），CBSは時刻\(t\)で実行可能状態になります．（バジェット\(c_s\)は必ず0より大きいです．）
  もし実行可能状態でない場合，CBSは時刻\(t\)でアイドル状態になります．
• ジョブ\(J_{i,j}\)が到着し，非周期サーバが実行可能状態になる時，そのジョブは任意の方法（例：FIFO）で待機状態のキューに挿入されます．
• ジョブ\(J_{i,j}\)が到着し，非周期サーバがアイドルになる時，もし\(c_s \geq (d_{s,k} - r_{i,j}) U_s\)の場合，非周期サーバは新しい絶対デッドライン\(d_{s,k+1} = r_{i,j} + T\)を設定し，\(c_s\)は最大値\(Q_s\)に再充填されます．
  そうでなければ，そのジョブは現在のバジェットを利用して，最後の非周期サーバの絶対デッドライン\(d_{s,k}\)で実行されます．
• ジョブが終了した時，もし次の待機状態のジョブがある場合，そのジョブは現在のバジェットと絶対デッドラインを利用して実行されます．
  もし待機状態のジョブがない場合，非周期サーバはアイドル状態になります．
• あらゆる時刻で，ジョブは最後の非周期サーバの絶対デッドラインを割り当てます．

CBSの例

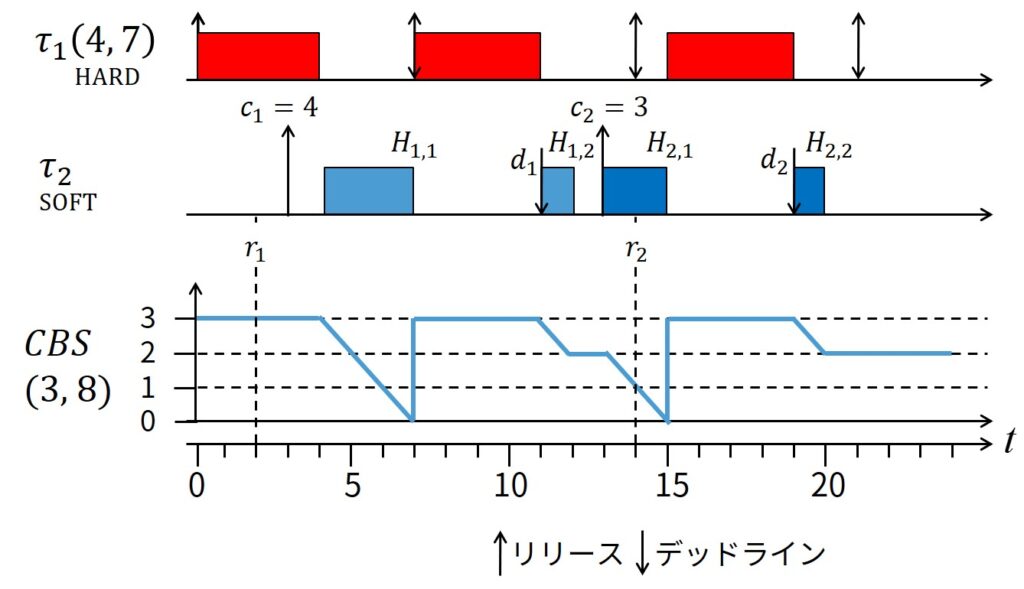
上図に，ハード周期タスク\(\tau_1\)（最悪実行時間\(C_1 = 4\)，周期\(T_1 = 7\)），CBS（バジェット\(Q_s=3\)，周期\(T_s=8\)）により実行されるソフト非周期タスク\(\tau_2\)のスケジュール例を示します．

4ユニット時間を要求する\(\tau_2 (J_{2,1})\)の最初のジョブは，非周期サーバがアイドル状態である時刻\(r_1=3\) に到着します．

\(c_s \geq (d_0 - r_1) U_s\)なので，そのジョブは絶対デッドライン\(d_1 = r_1 + T_s = 11\)が割り当てられ，\(c_s\) は\(Q_s = 3\)に再充填されます．

時刻\(t = 7\)では，バジェットが空になったので，新しい絶対デッドライン\(d_2 = d_1 + T_s = 19\) が生成され，\(c_s\)は再充填されます．

非周期サーバの絶対デッドラインが延期されたので，\(\tau_1\)は最も早い絶対デッドラインを持つタスクになるので，終了するまで実行します．

次に，\(\tau_2\)は再開し，ジョブ\(J_{2,1}\)（絶対デッドライン\(d_2=19\)）は時刻\(t=12\)で終了し，\(c_s = 2\)が残ります．

タスク\(\tau_2\)の2番目のジョブは時刻\(r_2 = 13\)に到着し，3ユニット時間を要求します．

\(c_s < (d_2 - r_2) U_s\)なので，最後の非周期サーバの絶対デッドライン\(d_2\)は，ジョブ\(J_{2,2}\)を実行するために利用されます．

時刻\(t=15\)では，非周期サーバのバジェットが空になり，新しい非周期サーバの絶対デッドライン\(d_3 = d_2 + T_s = 27\) が生成され，\(c_s\) が\(Q_s = 3\) に再充填されます．

この理由により，\(\tau_1\)が最高優先度タスクになり，時刻\(t=19\)まで実行して，ジョブ\(J_{1,3}\)が終了します．

また，時刻\(t=19\)では，\(\tau_2\)が実行開始し，時刻\(t=20\)でジョブ\(J_{2,2}\)が終了し，\(c_s = 2\)が残ります．

CBSにおいてジョブ\(J_j\)が時間変動する絶対デッドライン\(d_j\)を割り当てられることは注目すべきことです．

また，その絶対デッドラインは，もしタスクが予約されたバンド幅より多くの実行時間を要求する場合，延期されます．

したがって，各々のジョブ\(J_j\)は，リリース時刻\(a_{j,k}\)と固定された絶対デッドライン\(d_{j,k}\)を持つ，複数のチャンク\(H_{j,k}\)から構成されていると考えることができます．

上図を利用して，CBSにより生成されたチャンクの例を示します．

表記を簡単にするために，非周期サーバにより生成された全てのチャンクを増加するインデックス\(k\)で示します．

（上図では，\(H_{1,1} = H_1\)，\(H_{1,2} = H_2\)，\(H_{2,1} = H_3\)，\(H_{2,2} = H_4\)）

CBSの形式的定義

CBSの形式的定義を提供するためには，以下を定義します．

• \(a_k\)と\(d_k\)をそれぞれ非周期サーバにより生成された\(k^{th}\)番目のチャンクのリリース時刻と絶対デッドライン
• \(c\)と\(n\)をそれぞれ実際の非周期サーバのバジェットと非周期サーバのキューにある待機状態のリクエスト（現在実行状態のリクエストを含む）

これらの変数は以下の値に初期化されます．

$$d_0 = 0, c = 0, n = 0, k = 0.$$

この表記を利用すると，非周期サーバの動作は以下のアルゴリズムで記述できます．

CBSの性質

提案されたCBSサービス機構は，実行時間が大きく変化するアプリケーション（例：マルチメディアアプリケーション）のサポートに適した，いくつかの興味深い特性を持っています．

最も重要なのはアイソレーションの性質で，以下の定理により形式的に表現されています．（証明はこちらの文献を参照．）

定理26.1：CBSのCPU利用率\(S\)は，パラメータ\((Q_s, T_s)\)を利用して\(U_s = Q_s/T_s\)と表される．このCPU利用率は実行するジョブの実行時間や到着パターンから独立している．

以下の補題は，ハードとソフトタスクで構成されるタスクセットのスケジュール可能を検証するためのシンプルな十分条件のテストを提供します．

補題26.1：合計CPU利用率\(U_p\)の\(n\)個の周期ハードタスクセットと合計CPU利用率\(U_s=\sum_{i=1}^m U_s\)の\(m\)個のCBSのセットにおいて，全体のセットは以下の条件を満たす場合においてのみEDFでスケジュール可能である．

$$U_p + U_s \leq 1$$

アイソレーションの性質は，バンド幅予約機構を利用することで，実行時間を簡単に制限できない（過負荷になる可能性がある）ソフトタスクにCPU時間の1部を割り当てることができます．

この結果の最も重要な帰着は，ソフトタスクの実行時間がわからない場合や，期待された負荷を超える場合でも，予め保証されたことに影響を与えることなくソフトタスクをハードタスクと一緒にスケジュールできることです．

アイソレーションの性質に追加して，CBSは以下の特徴を持っています．

• もし提供されるタスク\(\tau_i\)が\(C_i \leq Q_s\)と\(T_i = T_s\)のようなパラメータ\((C_i, T_i)\)を持つ場合，CBSはEDFとして動作します．これは形式的には以下の補題で述べられています．

  補題26.2：パラメータ\((C_i, T_i)\)を持つハードタスク\(\tau_i\)は，\(\tau_i\)がEDFでスケジュール可能な場合においてのみ，パラメータ\(C_i \leq Q_s\)と\(T_i = T_s\)を持つCBSでスケジュール可能である．

  証明：ハードタスクの任意のジョブに対して，\(r_{i,j+1} - r_{i,j} \geq T_i\)と\(c_{i,j} \leq Q_s\)が成立します．
  CBSの定義により，各々のハードジョブは絶対デッドライン\(d_{i,j} = r_{i,j} + T_i\)が割り当てられ，バジェット\(C_i \leq Q_s\)でスケジュールされます．
  さらに，\(c_{i,j} \leq Q_s\)なので，バジェットが空になることなく，各々のジョブは実行終了します．
  したがって，ジョブに割り当てられた絶対デッドラインは決して延期されず，EDFが使用している絶対デッドラインと正確に同じになります．□

• CBSは早期終了による空き時間を回収します．
  これは，バジェットが空になるとすぐに再充填され，非周期サーバの絶対デッドラインが延期されることに起因しています．
  このように，非周期サーバのバジェットを利用して，現在の絶対デッドラインで待機状態の非周期タスクを実行できます．
  CBSが提供するタスクの実行時間の統計的分布を知ることで，確率的なデッドライン（各々のジョブがデッドラインまでに終了する確率）に基づくQoS保証を行うことが可能となる．
  そのような統計的解析は，こちらの文献を参照．

CBSのパラメータの算出

本章では，タスクの応答時間に対するCBSのパラメータ\((Q_s, T_s)\)の効果を評価するための統計的研究を紹介し，タスクの平均応答時間を最小化するパラメータを算出する手法を提案する．

バンド幅\(U_s\)を持つCBSにより実行される実行時間\(C_i\)を持つジョブの最悪応答時間\(R_i\)は，非周期サーバのバジェット\(Q_s\)の関数で表現されます．

分かりやすくするために，\(R_i\)は最初にオーバヘッドを無視して導出され，次にオーバヘッドを考慮したものに修正します．

CBSの解析から，タスクセットがスケジュール可能であれば，つまり，もし合計CPU利用率が100%未満であれば，ジョブは現在の非周期サーバの絶対デッドラインでデッドラインミスしないことがわかります．

したがって，最大応答時間\(R_i\)は，システム内の他のタスクが非周期サーバ上で最大の干渉時間になった時に発生します．

もし提供されたジョブの計算時間\(C_i\)がサーバのバジェット\(Q_s\)の倍数であれば，ジョブは非周期サーバのデッドライン時刻に終了します．

すなわち，以下の場合です．

$$R_i = \frac{C_i}{Q_s} T_s = \frac{C_i}{U_s}.$$

より一般的には，ジョブの実行時間\(C_i\)がバジェット\(Q_s\)の倍数でない場合，ジョブの最後の部分は非周期サーバのデッドラインに終了しません．

しかし，下図に示すように，デッドラインまでには最大での\(\Delta_i\)ユニット時間で終了します．

$$\Delta_i = \left\lceil \frac{C_i}{Q_s} \right\rceil Q_s - C_i$$

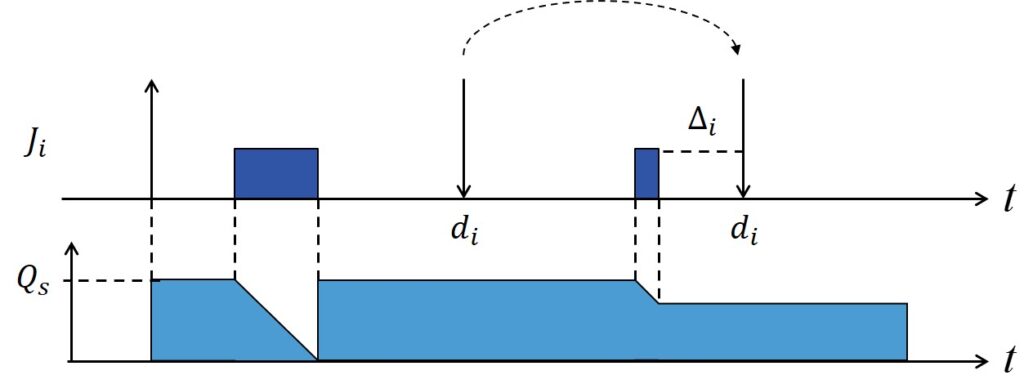
したがって，ジョブの応答時間は下式になります．

\begin{eqnarray}
R_i &=& \left\lceil \frac{C_i}{Q_s} \right\rceil T_s - \Delta_i \\
&=& \left\lceil \frac{C_i}{Q_s} \right\rceil T_s - \left( \left\lceil \frac{C_i}{Q_s} \right\rceil Q_s - C_i \right) \\
&=& C_i + \left\lceil \frac{C_i}{Q_s} \right\rceil (T_s - Q_s) \tag{26.1}
\end{eqnarray}

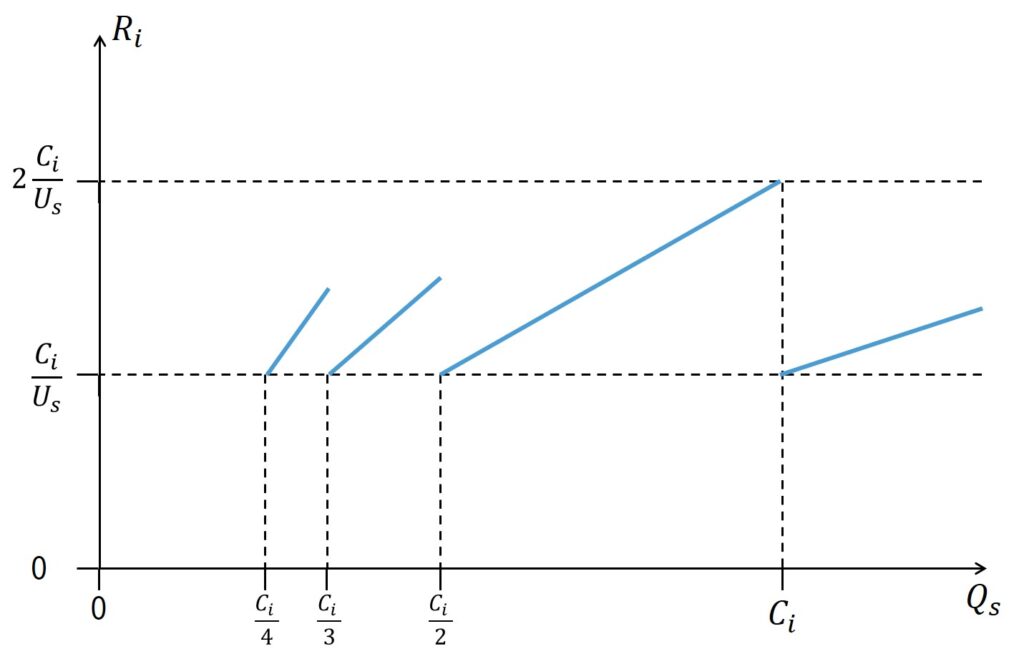
上図に，バジェットの関数としてのCBSの最悪応答時間を示します．

一定の実行時間\(C_i\)を持つジョブの場合，最短応答時間は\(C_i/U_i\)になり，\(C_i\)が\(Q_s\)の倍数である時に達成できることは明らかです．

しかし，実際には，タスクの実行時間が変動し，デッドライン延期によるバンド幅予約機構により，応答時間の変動が発生します．

また，平均実行時間と比較してバジェットを非常に小さくすることで，このような変動を減らすことで，理想的な非周期サーバに近づくことができます．

残念ながら，バジェットが小さい（非周期サーバの周期が短い）と，ジョブは多くの小さなチャンク（かたまり）に分割され，実行時のオーバヘッドが増えてしまいます．

結果として，非周期サーバの粒度\(T_s\)を適切に設定するためには，実行時のオーバヘッドを分析しなければなりません．

実行時のオーバヘッドを考慮

バジェットが空になると，非周期サーバのデッドラインを延期してしまうので，ジョブは最も早い絶対デッドラインを持つ他のタスクによりプリエンプションされます．

もし\(\epsilon\)がコンテキストスイッチに必要な時間を表す場合，CBSによって導入されるオーバヘッドは，非周期サーバのバジェットからこの時間を引くことで考慮することができます．

したがって，式\((26.1)\)は下式に修正することができます．

\begin{eqnarray}
R_i &=& C_i + \left\lceil \frac{C_i}{Q_s - \epsilon} \right\rceil (T_s - Q_s + \epsilon) \\
&=& C_i + \left\lceil \frac{C_i}{T_s U_s - \epsilon} \right\rceil (T_s - T_s U_s + \epsilon) \tag{26.2}
\end{eqnarray}

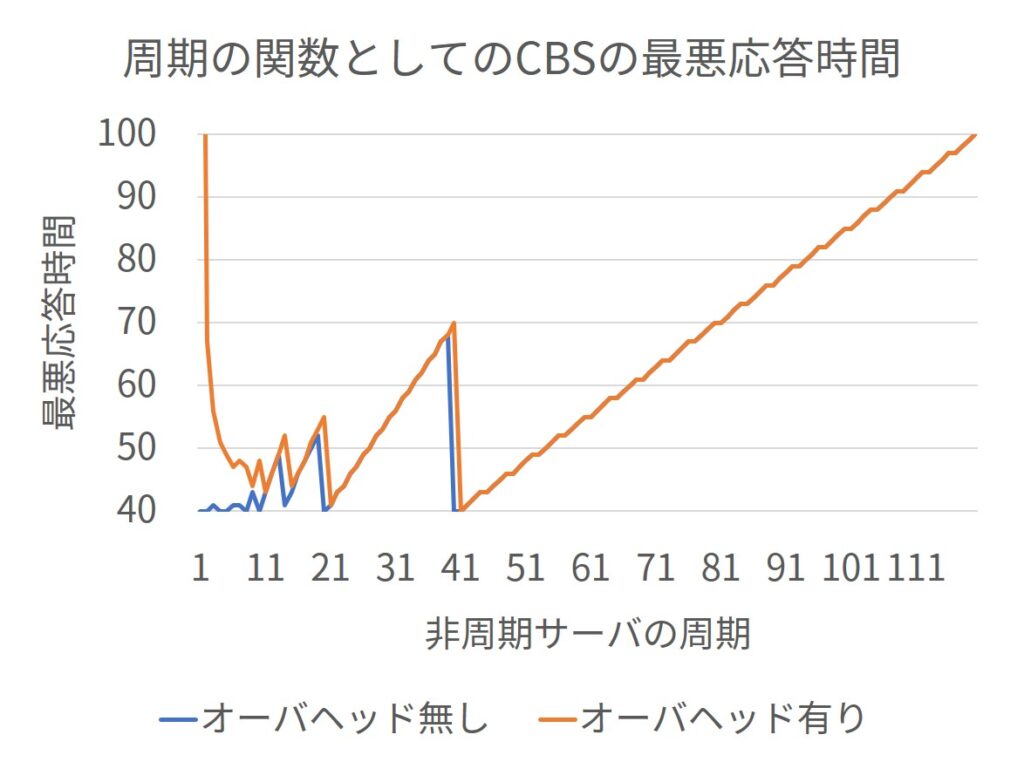
上図に，オーバヘッドの有無にかかわらず，周期の関数としてのCBSの最悪応答時間を示します．

式\((26.2)\)は，\(C_i = 10\)，\(U_s = 0.25\)，\(\epsilon = 0.2\)でプロットされています．

プロットから明らかなように，オーバヘッドは周期の短い値を利用することを防ぎます．

したがって，応答時間を最短にする非周期サーバの周期の値を見つけることは興味深いことです．

応答時間の確率分布関数を計算するためには，実際にはジョブの実行時間\(C_i\)の関数として応答時間を表現する必要があることに注意してください．

上図のプロットを作成するためのコードは以下になります．

実行結果は以下になります．

\(C_i = 10\)，\(U_s = 0.25\)，\(\epsilon = 0.2\)を入力しています．

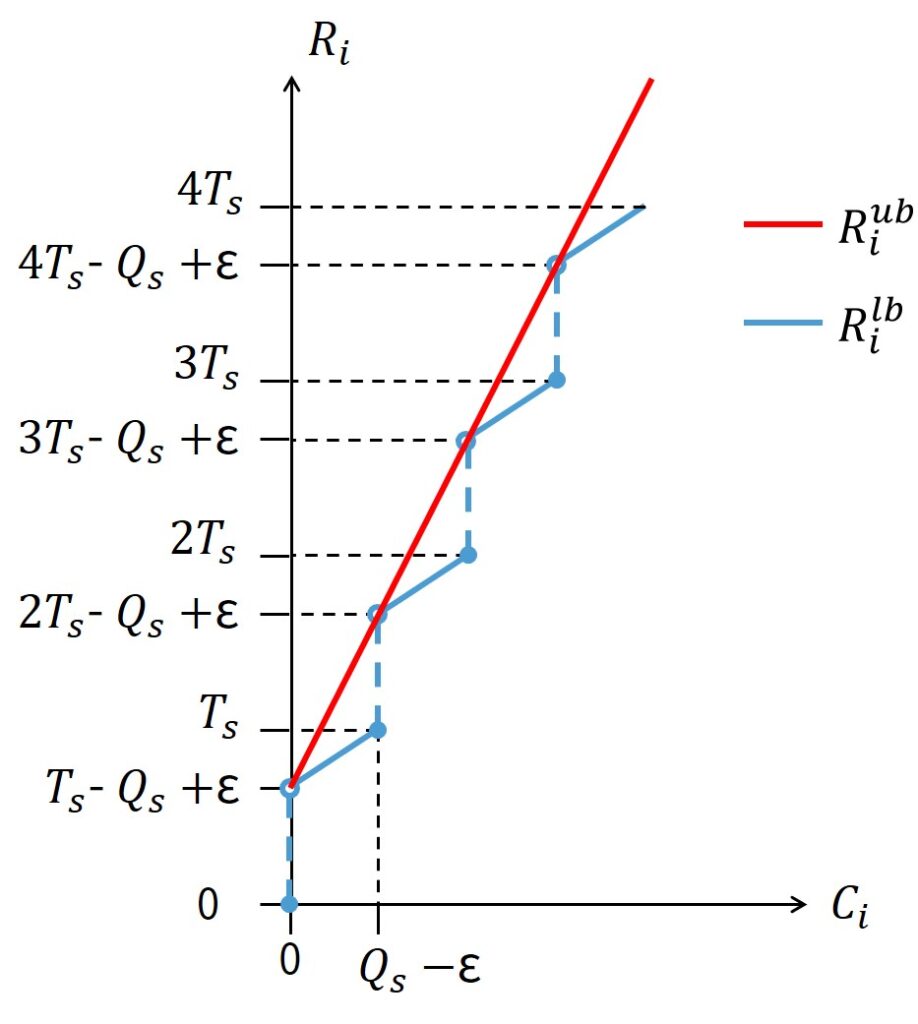
上図にジョブの実行時間の関数としてのCBSの最悪応答時間を示します．

応答時間\(R_i\)は，下式で上限を解析できます．

$$R_i^{ub} = T_s - Q_s + \epsilon + \frac{T_s}{Q_s - \epsilon} C_i$$

また，下式で下限を解析できます．

$$R_i^{lb} = \frac{T_s}{Q_s - \epsilon} C_i$$

ここで，タスクの平均応答時間\(R_i\)が最小になるように，最適なCBSパラメータを選択する問題を考えます．

この目的のために，確率密度関数（p.d.f.）\(f_C (c)\)と実行時間が\(c\)以下である確率を表すそれぞれの累積分布関数（c.d.f.）\(F_C (c)\)を持つと仮定します．

すなわち，下式になります．

$$F_C (c) = \int_0^c f_C(x) dx $$

平均値\(R_i\)の最小化は一般的に複雑すぎるので，その線形上限\(R_i^{ub}\)を最小化する問題を考えます．

この場合，平均応答時間\(R_i^{avg}\)は下式で算出します．

\begin{eqnarray}
R_i^{avg} &=& \int_0^{+\infty} \left( T_s - Q_s + \epsilon + \frac{T_s}{Q_s - \epsilon} x \right) f_C (x) dx \\
&=& T_s - Q_s + \epsilon + \frac{T_s}{Q_s - \epsilon} C^{avg} \\
&=& T_s (1 - U_s) + \epsilon + \frac{T_s}{T_s U_s - \epsilon} C^{avg}
\end{eqnarray}

したがって，平均応答時間\(R_i^{avg}\)を最小化する期間\(T_s\)は，単純な関数解析によって算出できます．

すなわち，下式になります．

$$\frac{dR_i^{avg}}{dT_s} = 1 - U_s - \frac{\epsilon}{(T_s U_s - \epsilon)^2} C^{avg}$$

上式が0になる時は下式が成立する時です．

$$T_s = \frac{1}{U_s} \left( \epsilon + \sqrt{\frac{\epsilon C^{avg}}{1 - U_s}} \right)$$

まとめ

今回は，CBSについて紹介しました．

CBSを学ぶとLinuxのリアルタイムスケジューリングポリシー「SCHED_DEADLINE」を理解できますので，是非覚えましょう！

具体的には，以下の内容を解説しました．

• CBSの定義
• CBSの例
• CBSの形式的定義
• CBSの性質
• CBSのパラメータの算出

リアルタイムシステムで使われているリアルタイムOSは，主にC言語で書かれています．

私にC言語の無料相談をしたいあなたは，公式LINE「ChishiroのC言語」の友だち追加をお願い致します．

私のキャパシティもあり，一定数に達したら終了しますので，今すぐ追加しましょう！

独学が難しいあなたは，元東大教員がおすすめするC言語を学べるオンラインプログラミングスクール5社で自分に合うスクールを見つけましょう．後悔はさせません！

次回はこちらからどうぞ．