【第25回】元東大教員から学ぶリアルタイムシステム「Improving TBS」

こういった私から学べます．

前回を読んでいない方はこちらからどうぞ．

リアルタイムシステムの記事一覧はこちらからどうぞ．

リアルタイムシステムで使われているリアルタイムOSは，主にC言語で書かれています．

私にC言語の無料相談をしたいあなたは，公式LINE「ChishiroのC言語」の友だち追加をお願い致します．

私のキャパシティもあり，一定数に達したら終了しますので，今すぐ追加しましょう！

独学が難しいあなたは，元東大教員がおすすめするC言語を学べるオンラインプログラミングスクール5社で自分に合うスクールを見つけましょう．後悔はさせません！

Improving TBS

Total Bandwidth Server（TBS）により利用されるデッドライン割り当てルールは，ハードリアルタイム環境で周期タスクと非周期タスクの両方を実行する上で，シンプルで効果的な手法です．

少し複雑になるだけで，このルールは非周期タスクの応答性を向上するように修正できます．

その重要のアイデアは，周期タスクがスケジュール可能な範囲内で，TBSにより割り当てられるデッドラインをできる限り短くすることです．

この手法をImproving TBSと呼びます．

もし\(d_k\)がTBSにより非周期タスクに割り当てられる絶対デッドラインの場合，絶対デッドライン\(d_k\)によりEDFでスケジュールされるので，新しい絶対デッドライン\(d_k^{'}\)はその非周期タスクの予想される最悪終了時刻\(f_k\)に設定することができます．

現在の予想される最悪終了時刻で新しい絶対デッドライン\(d_k^{'}\)を設定することがスケジュール可能性を低下させないことを，以下の補題で示します．

補題25.1：\(\sigma\)をタスクセット\(\cal{T}\)（非周期ジョブ\(J_k\)は絶対デッドライン\(d_k\)を割り当て）のリアルタイム性を保証可能（feasible）なスケジュール，\(f_k\)を\(\sigma\)における\(J_k\)の終了時刻とする．もし\(d_k\)が\(d_k^{'}=f_k\)で代用する場合，EDFで生成される新しいスケジュール\(\sigma'\)はスケジュール可能である．

証明：\(d_k\)が\(d_k^{'}=f_k\)で代用した後でも\(\sigma\)はスケジュール可能で，全ての他の絶対デッドラインは変更されません．

なので，EDFの最適性は保証され，\(\sigma'\)はまたスケジュール可能です．□

絶対デッドラインを短くする処理は，周期タスクセットのスケジュール可能性を保証できる範囲で，これ以上の向上ができなくなるまで，各々の新しい絶対デッドラインに再帰的に適用することができます．

もし\(d_k^s\)がステップ\(s\)で非周期タスク\(J_k\)に絶対デッドラインを割り当てて，\(f_k^s\)は（\(d_k^s\)で達成される）現在のEDFのスケジュールで対応する終了時刻とした場合，新しい絶対デッドライン\(d_k^{s+1}\)は時刻\(f_k^s\)で設定されます．

各々のステップで，タスクセットのスケジュール可能性は補題25.1で保証されます．

\(d_k=d_k^{s-1}\)または複雑度の上限をシステム設計者により定義される最大の上限数になった場合，この絶対デッドライン割り当てアルゴリズムは停止します．

\(f_k^s\)の正確な評価は，\(d_k^s\)でスケジュールされる非周期タスク\(J_k\)の終了時刻までの全体のスケジュールを要求することに注意して下さい．

しかし，絶対デッドラインを短くするために\(f_k^s\)の正確な値を評価する必要はありません．

以下の上限が利用できます．

$$\tilde{f_k^s} = t + C_k^a + I_p (t, d_k^s) \tag{25.1}$$

ここで，各々のパラメータの説明は以下になります．

• \(t\)：（非周期タスク\(J_k\)のリリース時刻\(r_k\)か前の非周期タスクの終了時刻に対応する）現在時刻
• \(C_k^a\)：\(J_k\)の最悪実行時間
• \(I_p (t, d_k^s)\)：区間\([t, d_k^s)\)における周期タスクのジョブによる\(J_k\)の干渉時間

\(\tilde{f_k^s}\)は\(f_k^s\)の上限になります．

この理由として，\(\tilde{f_k^s}\)は\(J_k\)と絶対デッドラインが\(d_k^s\)より早い全ての周期タスクのジョブが実行を終了する時刻になるからです．

したがって，\(f_k^s \leq \tilde{f_k^s}\)が成立します．

式\((25.1)\)の干渉時間\(I_p(t, d_k^s)\)は\(I_a(t, d_k^s)\)と\(I_f(t, d_k^s)\)の合計になります．

• \(I_a(t, d_k^s)\)：絶対デッドラインが\(d_k^s\)より早い現在実行可能状態の周期タスクのジョブによる干渉時間
• \(I_f(t, d_k^s)\)：\(d_k^s\)より早い絶対デッドラインを持つ時刻\(t\)より後にリリースされる周期タスクのジョブによる未来の干渉時間

したがって，下式になります．

$$I_a(t, d_k^s) = \sum_{\tau_i,\ active,\ d_i < d_k^s} c_i(t) \tag{25.2}$$

$$I_f(t, d_k^s) = \sum_{i=1}^{n} \max(0, \left\lceil \frac{d_k^s - next\_r_i(t)}{T_i} \right\rceil - 1)C_i \tag{25.3}$$

ここで，\(next\_r_i(t)\)はタスク\(\tau_i\)の次の周期タスクのジョブがリリースされる時刻\(t\)より遅い時刻を表します．

もし周期タスクが時刻0で同期的にリリースされる場合，以下が成立します．

$$next\_r_i(t) = \left\lceil \frac{t + 1}{T_i} \right\rceil T_i$$

\(I_a\)と\(I_f\)は\(\mathcal{O}(n)\)の計算量で算出できるので，絶対デッドライン割り当てアルゴリズムの全体の計算量は\(\mathcal{O}(Nn)\)になります．

ここで，\(N\)はTBSにより割り当てられた初期値の絶対デッドラインを短くするアルゴリズムにより実行される最大ステップ数になります．

\(\tilde{f_k^s}\)は，もし絶対デッドライン\(d_k^s\)と一致する場合，実際の最悪終了時刻になります．

補題25.2：あらゆるリアルタイム性を保証可能（feasible）なスケジュールにおいて，\(\tilde{f_k^s}=d_k^s\)の場合にのみ\(\tilde{f_k^s}=f_k^s\)が成立する．

証明：\(\tilde{f_k^s}=d_k^s\)で\(\tilde{f_k^s}>f_k^s\)の場合，リアルタイム性を保証可能（feasible）なスケジュール\(\sigma\)が存在します．

\(\tilde{f_k^s}\)は\(J_k\)と\(d_k^s\)より早い絶対デッドラインを持つ全ての周期タスクのジョブが実行を終了する時刻なので，\(\tilde{f_k^s}\)が\(\tilde{f_k^s}=d_k^s\)より早い絶対デッドラインを持つ周期タスクのジョブの終わりと一致することを\(\tilde{f_k^s}>f_k^s\)は意味します．

すなわち，このジョブはデッドラインミスするので，矛盾します．

したがって，補題は証明されました．□

Improving TBSの例

以下の例で絶対デッドライン割り当てアルゴリズムを示します．

タスクセットは2つの周期タスク\(\tau_1\)と\(\tau_2\)（周期はそれぞれ3と4，最悪実行時間はそれぞれ1と2）から構成されます．

1つの非周期ジョブ\(J_k\)が時刻2に到着し，2ユニット時間を要求します．

周期タスクセットのCPU利用率は\(U_p=5/6 (=1/3+2/4)\)，非周期タスクのバンド幅は\(U_s=1/6\)になります．

非周期タスクが時刻2に到着した時，TBSで算出される絶対デッドラインは\(d_k^0 = r_k + C_k^a / U_s=14\)になります．

このデッドライン割り当てを利用してEDFにより生成されるスケジュールは，下図になります．

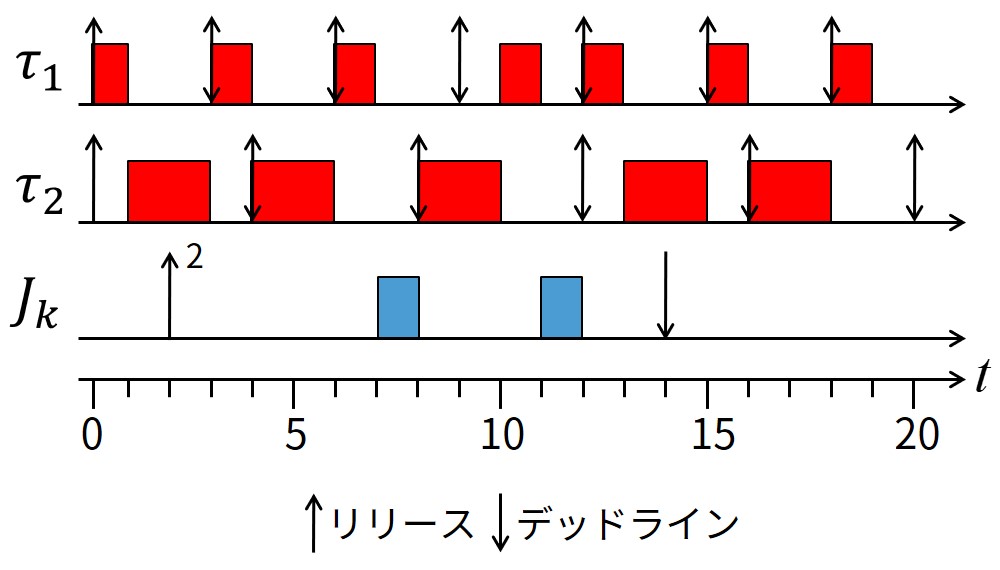
式\((25.2)\)，\((25.3)\)を適用すると，\(I_a\)と\(I_f\)はそれぞれ以下になります．

\begin{eqnarray}
I_a(2, 14) &=& c_2(2) = 1 \\
I_f(2, 14) &=& 3C_1 + 2C_2 = 7
\end{eqnarray}

式\((25.1)\)より，\(d_k^1\)は以下になります．

$$d_k^1 = \tilde{f_k^0} = t + C_k^a + I_a + I_f = 12$$

このケースでは，非周期タスクは時刻\(t=12\)で終了することがわかります．

この理由として，周期タスクは，（最後まで実行を強いられる）非周期タスクに利用できるアイドル時間を余らせないからです．

step	\(d_k^s\)	\(f_k^s\)
0	14	12
1	12	9
2	9	8
3	8	6
4	6	5
5	5	5

上表に，デッドライン近似アルゴリズムの各々のステップで評価される一連の絶対デッドラインを示します．

この例では，非周期タスクの最短のデッドラインを発見するために6つのステップが必要になります．

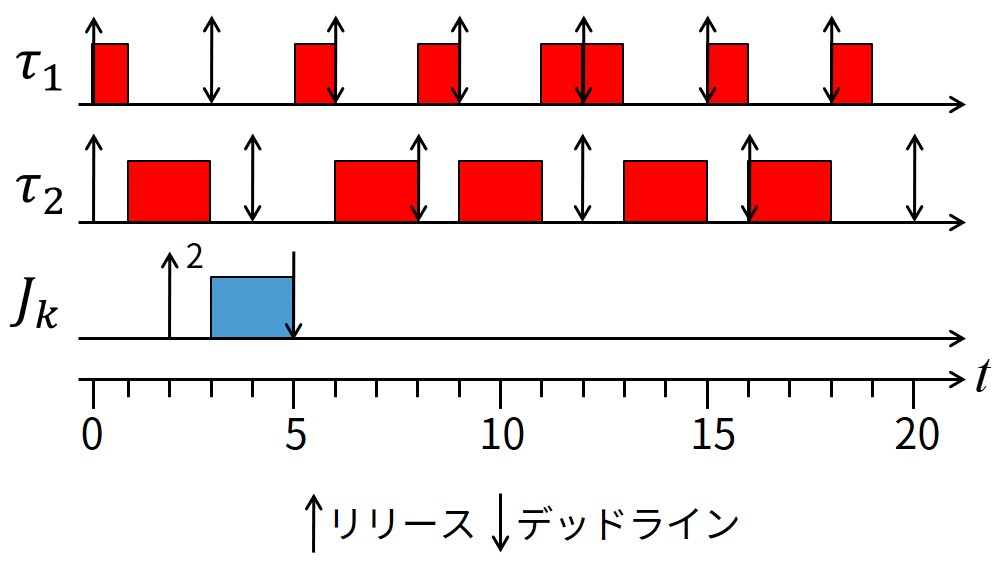
上図に最短の絶対デッドライン\(d_k^* = d_k^5 = 5\)を利用したEDFのスケジュールを示します．

時刻\(t=19\)で最初のアイドル時間になりますが，全体のタスクセットがスケジュール可能であることを示していることに注意して下さい．

Improving TBSの最適性

タスクの平均実行時間が最悪実行時間と同じである限り，デッドライン割り当て手法は最適性を達成し，各々の非周期タスクの最短応答時間になります．

この想定において，以下の定理が証明されています．

定理25.1：\(\sigma\)をタスクセット\(\cal{T}\)においてEDFで生成されるリアルタイム性を保証可能（feasible）なスケジュール，\(f_k\)を絶対デッドライン\(d_k\)を持つ\(\sigma\)でスケジュールされる非周期タスク\(J_k\)の終了時刻とする．もし\(f_k = d_k\)の場合，\(f_k = f_k^*\)（\(f_k^*\)はあらゆる他のfeasibleなスケジュールで達成可能な最短終了時刻）になる．

証明：\(f_k = d_k\)を想定し，\(r_0\)を区間\([r_0, d_k)\)において\(J_k\)と\(d_k\)より早い絶対デッドラインを持つタスクによりCPUがフル利用される最も早い時刻とします．

したがって，\(\sigma\)において，\(d_k\)は\(J_k\)と\(d_k\)より早い絶対デッドラインを持つ全てのジョブが実行を終了する時刻とします．

\(J_k\)が\(f_k' < d_k\)を満たすあらゆるスケジュール\(\sigma'\)において，feasibleでないことを示します．

実際，\([r_0, d_k)\)はCPUをフル利用され，\(f_k' < d_k\)を満たすので，\(\sigma'\)において，\(d_k\)は\(d_k\)より早い絶対デッドラインを持つ周期タスクのジョブの終了時刻でなければなりません．

※非周期タスクはFirst-Come First-Served（FCFS）で実行されるので，時刻\(d_k\)は非周期タスクの終了時刻になりません．

結果として，\(\sigma'\)はfeasibleでありません．

したがって，定理は証明されました．□

まとめ

今回は，Improving TBSについて紹介しました．

具体的には，以下の内容を解説しました．

• Improving TBSの特徴
• Improving TBSの例
• Improving TBSの最適性

リアルタイムシステムで使われているリアルタイムOSは，主にC言語で書かれています．

私にC言語の無料相談をしたいあなたは，公式LINE「ChishiroのC言語」の友だち追加をお願い致します．

私のキャパシティもあり，一定数に達したら終了しますので，今すぐ追加しましょう！

独学が難しいあなたは，元東大教員がおすすめするC言語を学べるオンラインプログラミングスクール5社で自分に合うスクールを見つけましょう．後悔はさせません！

次回はこちらからどうぞ．