【日本語訳】Proximal Policy Optimization Algorithms【近傍方策最適化】【OpenAI】

こういった悩みにお答えします．

こういった私から学べます．

AIのプログラミング言語「C++/Python言語」を学べるおすすめのWebサイトを知りたいあなたはこちらからどうぞ．

独学が難しいあなたは，AIを学べるオンラインプログラミングスクール3社で自分に合うスクールを見つけましょう．後悔はさせません！

国内・海外のAIエンジニアのおすすめ求人サイトを知りたいあなたはこちらからどうぞ．

国内・海外のプロンプトエンジニアのおすすめ求人サイトを知りたいあなたはこちらからどうぞ．

Proximal Policy Optimization Algorithmsの日本語訳を紹介します．

OpenAIの近傍方策最適化（PPO：Proximal Policy Optimization）がわかります．

※図表を含む論文の著作権はProximal Policy Optimization Algorithmsの著者に帰属します．

Proximal Policy Optimization Algorithmsの目次は以下になります．

• Abstract
• 1章：Introduction
• 2章：Background: Policy Optimization
• 3章：Clipped Surrogate Objective
• 4章：Adaptive KL Penalty Coefficient
• 5章：Algorithm
• 6章：Experiments
• 7章：Conclusion
• 8章：Acknowledgements
• References
• 付録A：Hyperparameters
• 付録B：Performance on More Atari Games

Proximal Policy Optimization Algorithmsを解説しつつ，私の考えも語ります．

Proximal Policy Optimization Algorithmsの概要と私の日本語訳は以下になります．

We propose a new family of policy gradient methods for reinforcement learning, which alternate between sampling data through interaction with the environment, and optimizing a "surrogate" objective function using stochastic gradient ascent.
環境との相互作用によるデータサンプリングと，確率的勾配上昇を用いた「代理」目的関数の最適化を交互に行う，強化学習のための新しい方策勾配法ファミリーを提案する．

Whereas standard policy gradient methods perform one gradient update per data sample, we propose a novel objective function that enables multiple epochs of minibatch updates.
標準的な方策勾配法は，データサンプルごとに1回の勾配更新を行うが，我々はミニバッチ更新の複数エポックを可能にする新しい目的関数を提案する．

The new methods, which we call proximal policy optimization (PPO), have some of the benefits of trust region policy optimization (TRPO), but they are much simpler to implement, more general, and have better sample complexity (empirically).
近傍方策最適化（PPO：Proximal Policy Optimization）と呼ぶこの新しい手法は，信頼領域方策最適化（TRPO：Trust Region Policy Optimization）の利点もあるが，実装がより簡単で，より一般的で，サンプル複雑度も優れている（経験的に）．

Our experiments test PPO on a collection of benchmark tasks, including simulated robotic locomotion and Atari game playing, and we show that PPO outperforms other online policy gradient methods, and overall strikes a favorable balance between sample complexity, simplicity, and wall-time.
我々の実験では，ロボットの運動シミュレーションやAtariゲームプレイなどのベンチマークタスクでPPOをテストし，PPOが他のオンライン方策勾配法を凌駕し，全体としてサンプル複雑性，単純性，ウォールタイムのバランスが取れていることを示す．

https://arxiv.org/abs/1707.06347

私の日本語訳の注意点は以下になります．

• 概要は英語と日本語を両方掲載しましたが，本文は私の日本語訳のみを掲載していること（英語で読みたいあなたは原文を読みましょう！）
• 基本的には原文の直訳だが，わかりにくい箇所は意訳や説明を追加している箇所があること
• 原文の「Acknowledgements」（謝辞）は省略していること
• 本文中に登場する表記「[Mni+15]」などは参考文献ですので，興味がある方は本記事の参考文献を参照されたいこと

それでは，Proximal Policy Optimization Algorithmsの本文を読みすすめましょう！

1章：Introduction（はじめに）

近年，ニューラルネットワークの関数近似を用いた強化学習において，いくつかの異なるアプローチが提案されている．

その代表的なものが，Deep Q-Learning[Mni+15]，「バニラ」方策勾配法（“vanilla” Policy Gradient Methods）[Mni+16]，信頼領域/自然方策勾配法（Trust Region/Natural Policy Gradient Methods）[Sch+15b]である．

しかし，スケーラブル（大規模モデルや並列実装に対応），データ効率，ロバスト（ハイパーパラメータのチューニングなしに様々な問題で成功する）な手法を開発するには，改善の余地がある．

Q-Learning（関数近似を用いる）は多くの単純な問題で失敗し，理解が不十分であり，バニラ方策勾配法はデータ効率と頑健性に劣る．

※DQNは，離散的な行動空間を持つArcade Learning Environment[Bel+15]のようなゲーム環境ではうまく機能するが，OpenAI Gym[Bro+16]やDuan et al.[Dua+16]で説明されているような連続制御ベンチマークでは，うまく機能しないことが実証されている．

また，信頼領域方策最適化（TRPO：Trust Region Policy Optimization）は比較的複雑であり，ノイズ（ドロップアウトなど）やパラメータ共有（方策と価値関数間，または補助タスク）を含むアーキテクチャとは互換性がない．

本論文では，一次最適化のみを用いながら，TRPOのデータ効率と信頼性の高い性能を達成するアルゴリズムを導入することで，現状を改善することを目指す．

我々は，確率比を切り詰めた新しい目的関数を提案し，これにより方策の性能の悲観的な推定値（すなわち下限）を形成する．

方策を最適化するために，方策からデータをサンプリングすることと，サンプリングされたデータに対して数エポックの最適化を実行することを交互に行う．

我々の実験では，様々な異なるバージョンの代理目的関数の性能を比較し，クリッピングした確率比のバージョンが最も良い性能を発揮することを発見した．

また，PPOを文献にあるいくつかの先行アルゴリズムと比較した．

連続制御タスクでは，PPOは比較したアルゴリズムよりも優れた性能を発揮した．

Atariでは，PPOはA2Cよりも（サンプルの複雑さの点で）大幅に性能が向上し，ACERと同様だが，より単純なものだとわかった．

2章：Background: Policy Optimization（バックグラウンド：方策最適化）

2.1節：Policy Gradient Methods（方策勾配法）

方策勾配法は，方策勾配の推定器を計算し，それを確率的勾配上昇アルゴリズムに差し込むことで動作する．

最もよく使われる勾配推定器は下式になる．

$$\hat{g} = \hat{\mathbb{E}}_t \left[\nabla_\theta \log \pi_\theta (a_t | s_t) \hat{A}_t \right]$$

ここで，\(\pi_\theta\)は確率的方策，\(\hat{A}_t\)はタイムステップtにおけるアドバンテージ関数の推定器である．

期待値\(\hat{\mathbb{E}}_t[...]\)は，サンプリングと最適化を交互に行うアルゴリズムにおいて，サンプルの有限バッチの経験平均を示す．

自動微分ソフトウェアを用いた実装では，方策勾配推定器を勾配とする目的関数を構築することで動作する．

推定器\(\hat{g}\)は，目的関数を微分することで得られる．

$$L^{PG}(\theta) = \hat{\mathbb{E}}_t \left[\log \pi_\theta (a_t | s_t) \hat{A}_t \right]$$

この損失\(L^{PG}\)に対して，同じ軌道で複数ステップの最適化を行うことは魅力的だが，そうすることは正当化されず，経験的にしばしば破壊的に大きな方策更新につながる（6.1節参照：結果は示していないが，「クリッピングやペナルティなし」設定と同等かそれ以上だった）．

2.2節：Trust Region Methods（信頼領域法）

TRPO[Sch+15b]では，方策更新のサイズに関する制約関数の下で目的関数（「代理」目的関数）が最大化される．

具体的には，下式である．

\begin{align*}
\underset{\theta}{\rm maximize} & \ \ \ \hat{\mathbb{E}}_t \left[\frac{ \pi_\theta (a_t | s_t)}{ \pi_{\theta_{old}} (a_t | s_t)} \hat{A}_t \right] \\
{\rm subject\ to} & \ \ \ \hat{\mathbb{E}}_t \left[ KL \left[\pi_{\theta_{old}} (\cdot | s_t), \pi_\theta (\cdot | s_t) \right] \right] \leq \delta
\end{align*}

ここで，\(\theta_{old}\)は更新前の方策パラメータのベクトルである．

この問題は，目的関数の線形近似と制約関数の二次近似を行った後，共役勾配アルゴリズムを用いて効率よく近似的に解くことができる．

TRPOを正当化する理論は，実際には制約関数の代わりにペナルティ関数を使う，つまり制約関数のない最適化問題を解くことを提案している．

$$\underset{\theta}{\rm maximize} \ \hat{\mathbb{E}}_t \left[\frac{ \pi_\theta (a_t | s_t)}{ \pi_{\theta_{old}} (a_t | s_t)} \hat{A}_t - \beta KL \left[ \pi_{\theta_{old}} (\cdot | s_t), \pi_\theta (\cdot | s_t) \right] \right] \tag{1}$$

上記をある係数\(\beta\)で計算する．

これは，ある代理目的関数（平均値の代わりに状態に対する最大KLを計算する）が，方策\(\pi\)の性能に対する下限（すなわち，悲観的な境界）を形成するという事実から導かれる．

TRPOがペナルティではなくハード制約関数を用いるのは，異なる問題，あるいは1つの問題であっても学習過程で特性が変化するような場合に，良好な性能を示す1つの値\(\beta\)を選ぶことが困難だからである．

したがって，TRPOの単調改善をエミュレートする一次アルゴリズムの目標を達成するためには，単に固定ペナルティ係数\(\beta\)を選択し，SGDでペナルティ付き目的関数の式（1）を最適化するだけでは不十分で，さらなる改良が必要であることが実験から示された．

3章：Clipped Surrogate Objective（クリッピング代理目的関数）

\(r_t(\theta)\)を確率比\(r_t(\theta) = \frac{ \pi_\theta (a_t | s_t)}{ \pi_{\theta_{old}} (a_t | s_t)}\)，\(r(\theta_{old})=1\)とする．

TRPOは「代理」目的関数を最大化する．

$$L^{CPI}(\theta) = \hat{\mathbb{E}}_t \left[\frac{ \pi_\theta (a_t | s_t)}{ \pi_{\theta_{old}} (a_t | s_t)} \hat{A}_t \right] = \hat{\mathbb{E}}_t \left[ r_t(\theta) \hat{A}_t \right] $$

上付き文字CPIは，この目的関数が提案されたConservative Policy Iteration（保守的方策反復）[KL02]を意味する．

制約関数がない場合，\(L^{CPI}\)を最大化すると，過度に大きな方策更新につながる．

そこで，\(r_t(\theta)\)を1から遠ざけるような方策の変更にペナルティを与えるために，この目的関数をどのように変更するかを検討することにする．

我々が提案する主な目的関数は以下の通りである．

$$L^{CLIP}(\theta) = \hat{\mathbb{E}}_t \left[ \min(r_t(\theta) \hat{A}_t, {\rm clip}(r_t(\theta), 1 - \epsilon, 1 + \epsilon) \hat{A}_t \right] $$

ここで，\(\epsilon\)はハイパーパラメータであり，例えば\(\epsilon = 0.2\)である．

この目的関数の動機は以下の通りである．

minの中の第1項は\(L^{CPI}\)である．

第2項は，\({\rm clip}(r_t(\theta), 1 - \epsilon, 1 + \epsilon) \hat{A}_t\)で，確率比をクリッピングすることで代理目的関数を修正し，\(r_t\)を区間\( [1 - \epsilon, 1 + \epsilon] \)の外に移動するインセンティブを除去する．

最後に，クリッピングされた目的関数とクリッピングされていない目的関数の最小値をとり，最終的な目的関数はクリッピングされていない目的関数の下限（すなわち，悲観的な境界）となるようにする．

この方式では，確率比の変化が目的関数を向上させる場合にのみ無視し，目的関数を悪化させる場合には含める．

なお，\(L^{CLIP}(\theta) = L^{CPI}(\theta)\)は，\(\theta_{old}\)付近（すなわちr = 1）で一次関数となるが，\(\theta\)が\(\theta_{old}\)から離れると両者は異なるものとなる．

図1は，\(L^{CLIP}\)の第1項（すなわち，1つのt）をプロットしたものである．

ただし，確率比rはアドバンテージが正か負かによって，\(1 - \epsilon\)か\(1 + \epsilon\)でクリッピングされる．

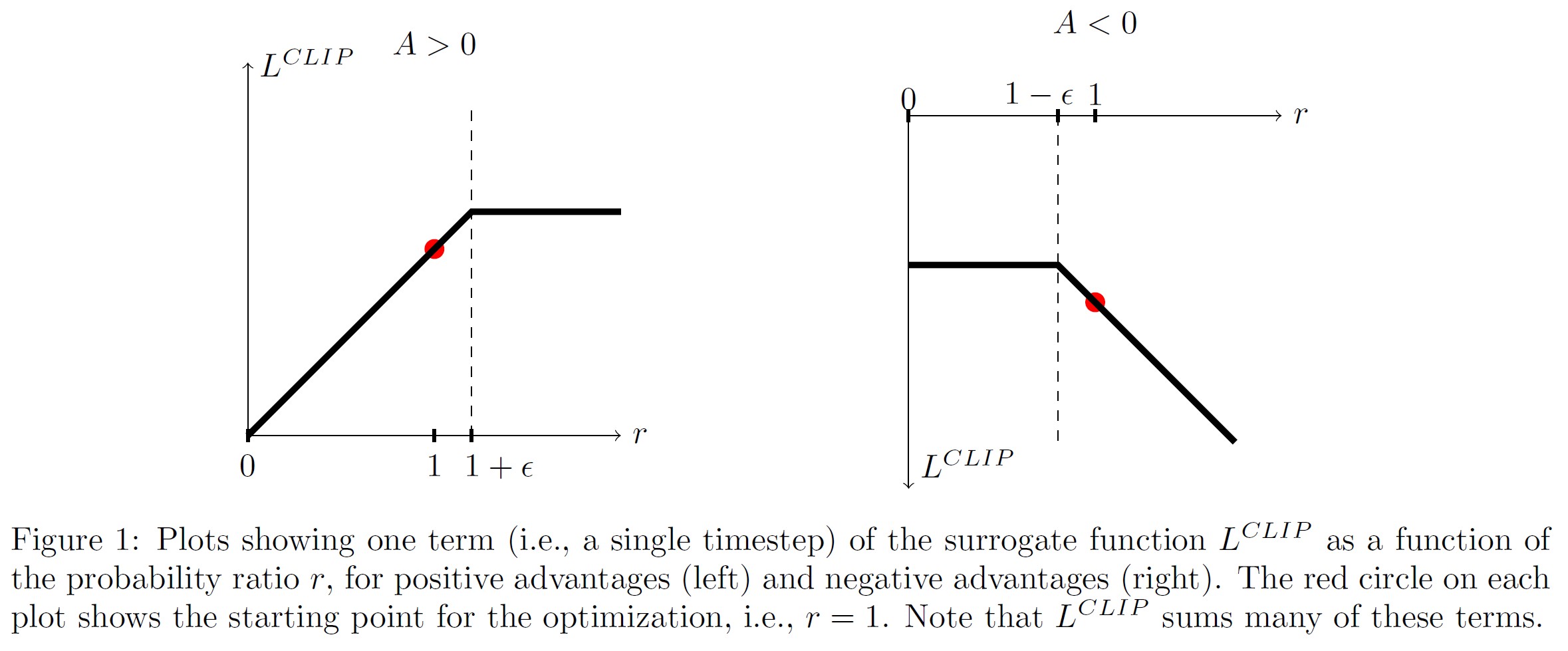
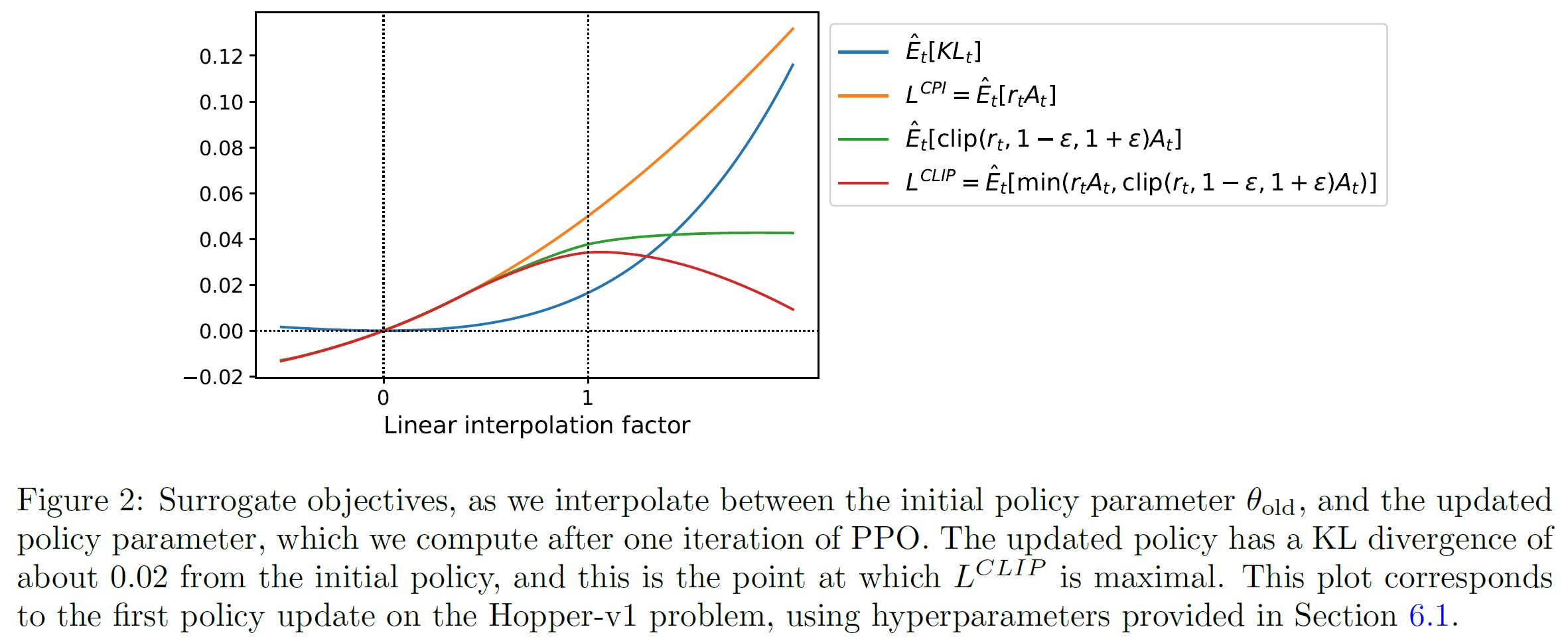
図2は，代理目的関数\(L^{CLIP}\)に関する直感的な情報を提供するものである．

これは，連続制御問題の近接方策最適化（これから紹介するアルゴリズム）によって得られる方策更新方向に沿って補間するときに，いくつかの目的関数がどのように変化するかを示している．

\(L^{CLIP}\)は\(L^{CPI}\)の下限であり，方策更新が大きすぎる場合のペナルティがあることがわかる．

4章：Adaptive KL Penalty Coefficient（適応型KLペナルティ係数）

もう一つのアプローチは，クリッピング代理目的関数の代替として，またはそれに加えて，KLダイバージェンスに対するペナルティを使用し，方策更新ごとにKLダイバージェンス\(d_{targ}\)のある目標値を達成するようにペナルティ係数を適応することである．

我々の実験では，KLペナルティはクリッピング代理目的関数よりも性能が悪いことがわかったが，重要なベースラインであるため，ここに記載した．

このアルゴリズムの最も単純なインスタンス化では，各方策更新で以下のステップを実行する．

• ミニバッチSGDの数エポックを使って，KLペナルティを受けた目的関数を最適化する．
  $$L^{KLPEN}(\theta) = \hat{\mathbb{E}}_t \left[\frac{ \pi_\theta (a_t | s_t)}{ \pi_{\theta_{old}} (a_t | s_t)} \hat{A}_t - \beta KL \left[ \pi_{\theta_{old}} (\cdot | s_t), \pi_\theta (\cdot | s_t) \right] \right] $$
• \(d= \hat{\mathbb{E}}_t \left[ KL \left[ \pi_{\theta_{old}} (\cdot | s_t), \pi_\theta (\cdot | s_t) \right] \right] \)を計算する．
  • \(d < d_{targ} / 1.5\)の場合，\(\beta \leftarrow \beta / 2\)
  • \(d > d_{targ} * 1.5\)の場合，\(\beta \leftarrow \beta * 2\)

更新された\(\beta\)は，次の方策更新に使用される．

この方式では，KLダイバージェンスが\(d_{targ}\)と大きく異なる方策更新が時々見られるが，これは稀であり，\(\beta\)はすぐに調整される．

上記のパラメータ1.5と2は発見的に選ばれたものであるが，アルゴリズムはそれに対してあまり敏感ではない．

\(\beta\)の初期値は別のハイパーパラメータであるが，アルゴリズムがすぐに調整するため，実際には重要ではない．

5章：Algorithm（アルゴリズム）

前章の代理損失は，典型的な方策勾配の実装を少し変更するだけで，計算と微分することができる．

自動微分法を用いる実装では，\(L^{PG}\)の代わりに\(L^{CLIP}\)または\(L^{KLPEN}\)という損失を構築し，この目的関数に対して確率的勾配上昇の複数ステップを実行するだけである．

分散削減されたアドバンテージ関数推定器を計算する技術の多くは，学習された状態値関数V(s)を使用する．

例えば，汎化アドバンテージ推定器[Sch+15a]や[Mni+16]の有限ホライズン推定器などである．

方策と価値関数の間でパラメータを共有するニューラルネットワークアーキテクチャを使用する場合，方策代理関数と価値関数誤差項を組み合わせた損失関数を使用する必要がある．

この目的関数は，過去の研究[Wil92; Mni+16]で提案されたように，十分な探索を保証するためにエントロピーボーナスを追加することでさらに拡張することができる．

これらの項を組み合わせることで，以下の目的関数が得られ，これは各反復で（ほぼ）最大化される．

$$L_t^{CLIP+VF+S}(\theta) = \hat{\mathbb{E}}_t \left[L_t^{CLIP}(\theta) - c_1 L_t^{VF}(\theta) + c_2 S \left[ \pi_\theta \right] (s_t) \right] $$

ここで，\(c_1\)，\(c_2\)は係数，Sはエントロピーボーナスを表し，\(L_t^{VF}\)は自乗誤差損失\((V_\theta(s_t) - V_t^{\rm targ})^2\)を表す．

[Mni+16]で汎化され，リカレントニューラルネットワークでの使用に適した方策勾配実装の1つのスタイルは，Tタイムステップ（Tはエピソード長よりはるかに小さい）の間方策を実行し，収集されたサンプルを更新に使用する．

このスタイルでは，タイムステップTの先を見ないアドバンテージ推定器が必要である．

[Mni+16]で使用された推定器は以下の通りである．

$$\hat{A}_t = -V(s_t) + r_t + \gamma r_{t+1} + ... + \gamma^{T-t+1} r_{T-1} + \gamma^{T-t} V(s_T) \tag{2}$$

ここで，tは与えられた長さTの軌跡セグメント内の[0, T]の時間インデックスを指定する．

この選択を汎化すると，汎化されたアドバンテージ推定器の切り捨てバージョンを使うことができ，これは，\(\lambda=1\)のとき，式（2）に帰結する．

\begin{align*}
&\hat{A}_t = \delta_t + (\gamma \lambda) \delta_{t+1} + ... + (\gamma \lambda)^{T-t+1} \delta_{T-1} \\
&{\rm where}\ \delta_t = r_t + \gamma V(s_{t+1}) - V(s_t)
\end{align*}

固定長の軌跡セグメントを使用する近接方策最適化（PPO：Proximal Policy Optimization）アルゴリズムを以下に示す．

各反復では，N（並列）ActorsのそれぞれがTタイムステップのデータを収集する．

そして，これらのNTタイムステップのデータで代理損失を構成し，Kエポックについて，ミニバッチSGD（または通常，より良い性能のために，Adam[KB14]）で最適化する．

6章：Experiments（実験）

6.1節：Comparison of Surrogate Objectives（代理目的関数の比較）

まず，異なるハイパーパラメータの下で，いくつかの異なる代理目的関数を比較する．

ここでは，代理目的関数である\(L^{CLIP}\)を，いくつかの自然なバリエーションとアブレーションされたバージョンと比較する．

\begin{align*}
{\rm No\ clipping\ or\ penalty:}\ & L_t(\theta) = r_t(\theta) \hat{A}_t \\
{\rm Clipping:}\ & L_t(\theta) = \min(r_t(\theta) \hat{A}_t, {\rm clip}(r_t(\theta)), 1 - \epsilon, 1 + \epsilon) \hat{A}_t \\
{\rm KL\ penalty\ (fixed\ or\ adaptive):}\ & L_t(\theta) = r_t(\theta) \hat{A}_t - \beta KL \left[\pi_{\theta_{\rm old}}, \pi_{\theta} \right]
\end{align*}

KLペナルティには，固定ペナルティ係数\(\beta\)を用いるか，ターゲットKL値\(d_{targ}\)を用いて4章で説明したように適応的な係数を用いるかのどちらかである．

なお，対数空間でのクリッピングも試したが，性能は変わらなかった．

各アルゴリズムのバリエーションについてハイパーパラメータを探索するため，アルゴリズムをテストするために，計算量の少ないベンチマークを選択した．

すなわち，OpenAI Gym[Bro+16]で実装され，MuJoCo[TET12]の物理エンジンを使用する7つの模擬ロボットタスクを使用した．

※7つの模擬ロボットタスクは，HalfCheetah，Hopper，InvertedDoublePendulum，InvertedPendulum，Reacher，Swimmer，Walker2dで，すべて「-v1」（バージョン1）である．

それぞれについて，100万タイムステップの訓練を行う．

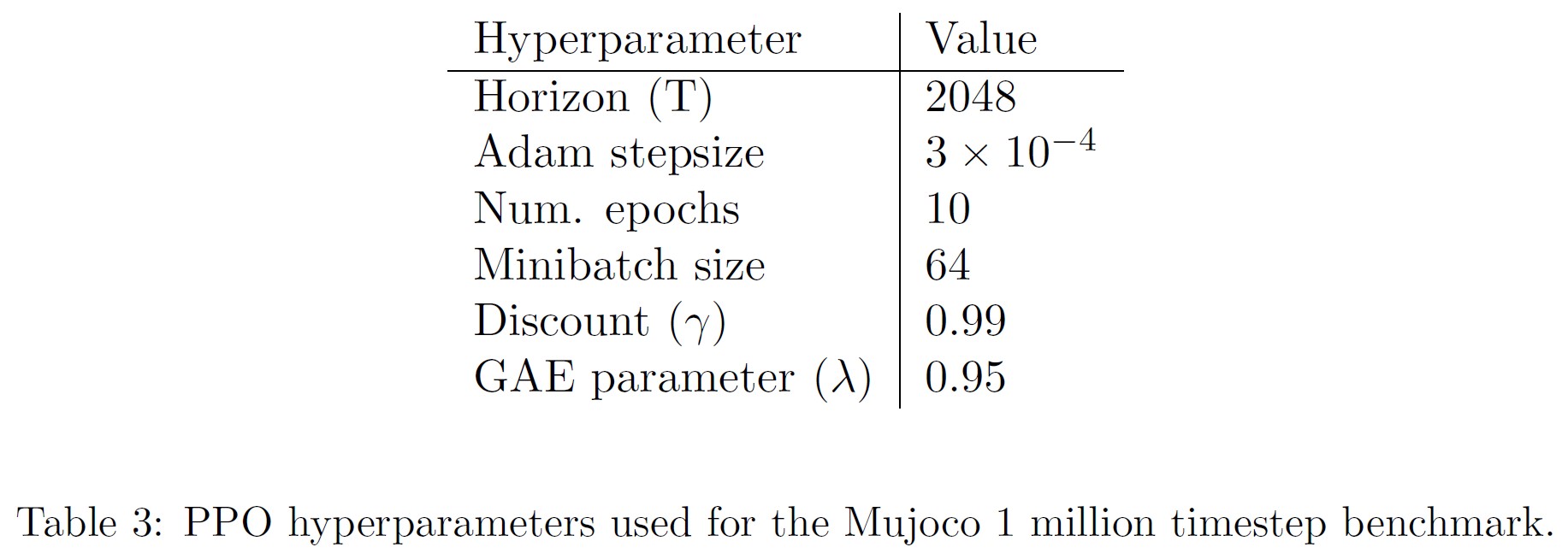
クリッピング\((\epsilon)\)とKLペナルティ\((\beta, d_{targ})\)に使用するハイパーパラメータを検索したほか，その他のハイパーパラメータは表3に示すとおりである．

※訳注：原文の「in in Table 3」は「in Table 3」の間違い．

方策を表現するために，[Sch+15b; Dua+16]に従って，64ユニットの2つの隠れ層とtanh非線形を持つ完全連結MLPを用い，ガウス分布の平均を出力し，標準偏差は可変とする．

方策と価値関数の間でパラメータを共有せず（従って係数\(c_1\)は無関係），エントロピーボーナスも使用しない．

各アルゴリズムは7つの環境すべてで実行され，それぞれ3つのランダムシードが使用された．

各アルゴリズムの実行は，直近の100エピソードの平均総報酬を計算することで得点化した．

各環境のスコアをシフトしてスケーリングし，ランダム方策が0，最良の結果が1となるようにし，21回の実行を平均して，各アルゴリズム設定に対して単一のスカラーを生成した．

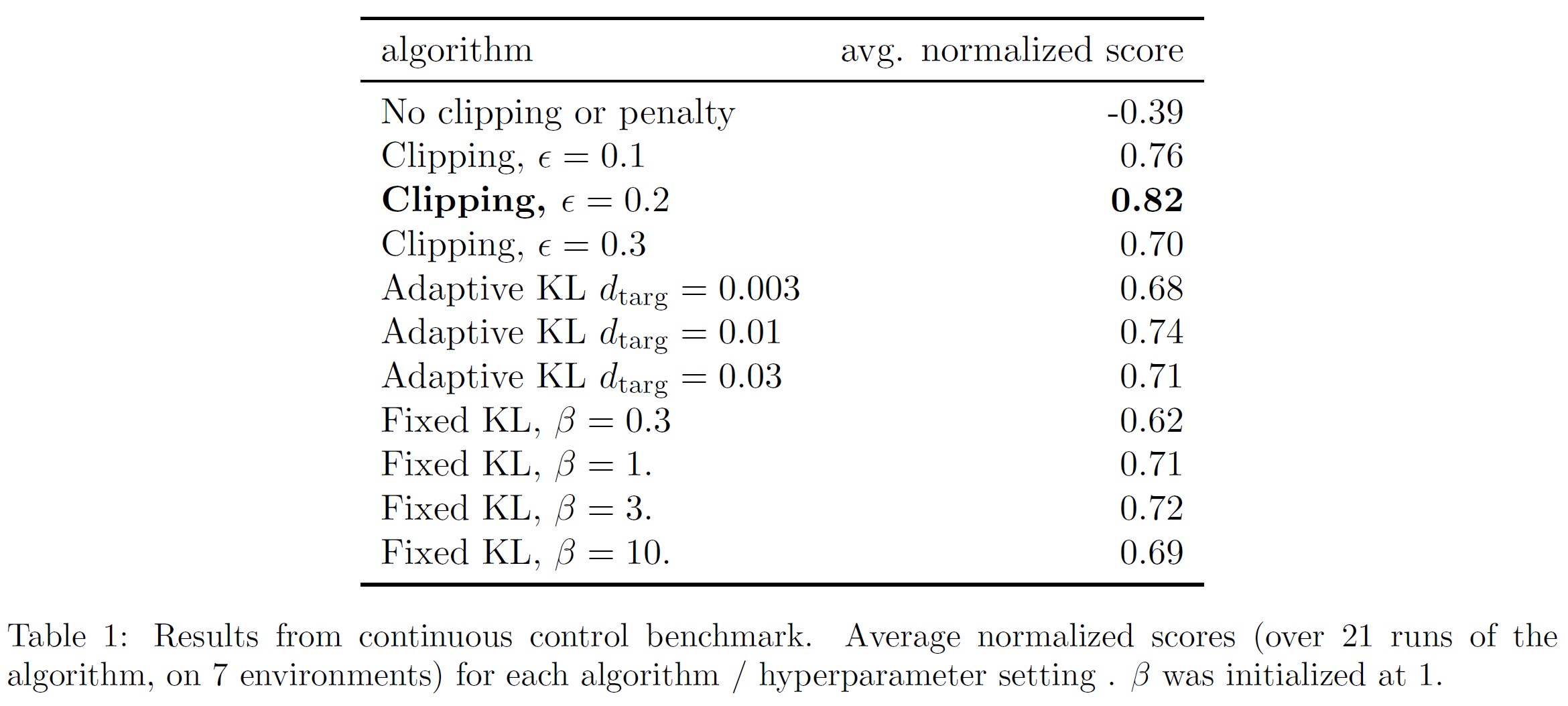
結果は表1に示す通りである．

なお，クリッピングやペナルティを設けない設定では，1つの環境（HalfCheetah）に対して，スコアが非常にマイナスになり，初期のランダム方策よりも悪くなっている．

6.2節：Comparison to Other Algorithms in the Continuous Domain（連続領域における他のアルゴリズムとの比較）

次に，PPO (3章の「クリッピング」代理目的関数を含む）を，連続問題に有効であると考えられている，文献にある他のいくつかの方法と比較する．

信頼領域方策最適化[Sch+15b]，クロスエントロピー法（CEM：Cross-Entropy Method）[SL06]，適応的ステップサイズ付きバニラ方策勾配，A2C[Mni+16]，信頼領域付きA2C[Wan+16]などのアルゴリズムを調整した実装と比較した．

※データの各バッチの後，Adamのステップサイズは，4章で示されたものと同様のルールを使用して，オリジナルの方策と更新された方策のKLダイバージェンスに基づいて調整される．実装は，https://github.com/berkeleydeeprlcourse/homework/tree/master/hw4で公開されている．

A2CはAdvantage Actor Criticの略で，A3Cの同期版であり，非同期版と同等かそれ以上の性能を持つことがわかった．

PPOについては，前節のハイパーパラメータを使用し，\(\epsilon = 0.2\)としている．

ほぼすべての連続制御環境において，PPOがこれまでの手法を上回ることがわかる．

※訳注：図3は本文中では参照されていませんが，こちらに配置しておきます．

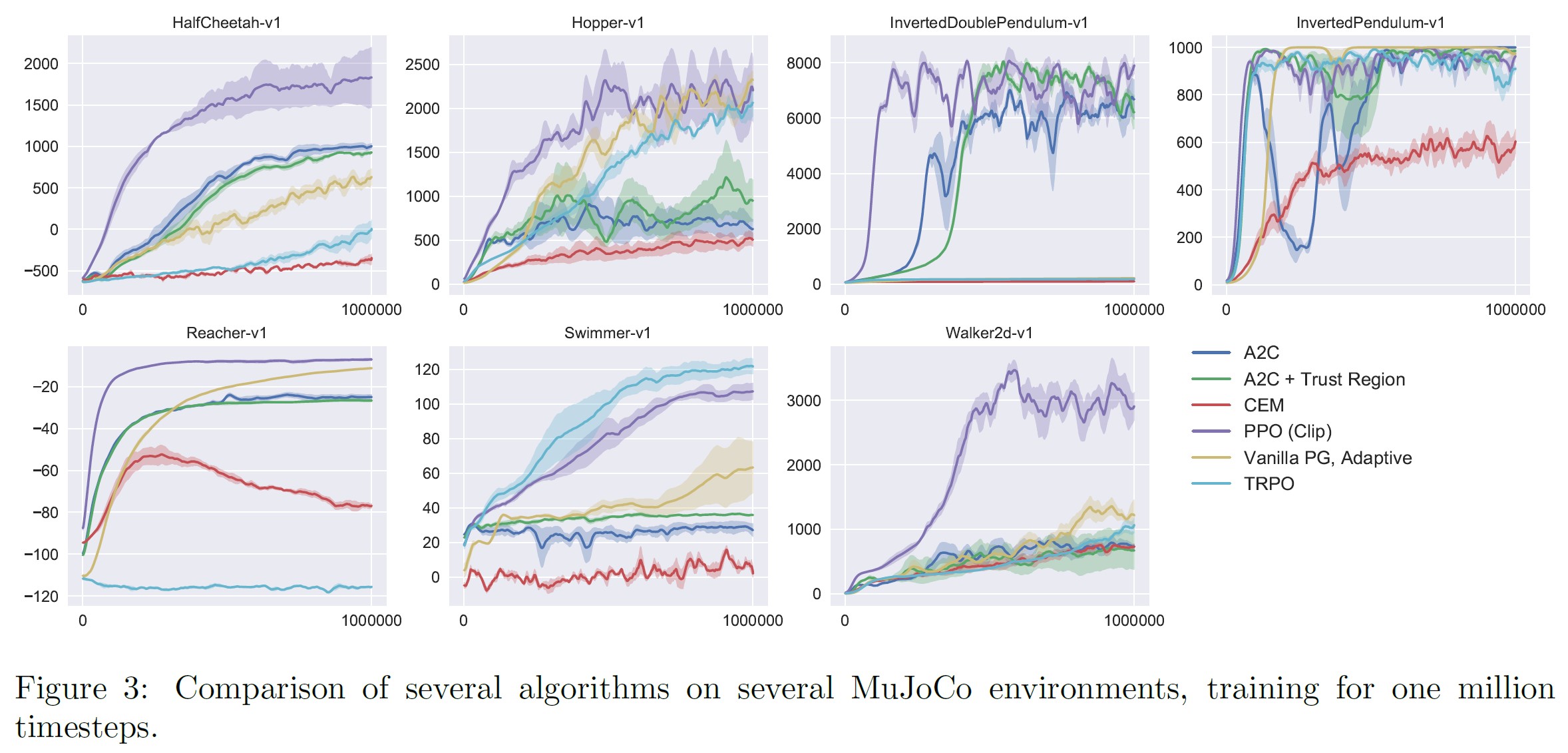
6.3節：Showcase in the Continuous Domain: Humanoid Running and Steering（連続領域でのショーケース：ヒューマノイドのランニングとステアリング）

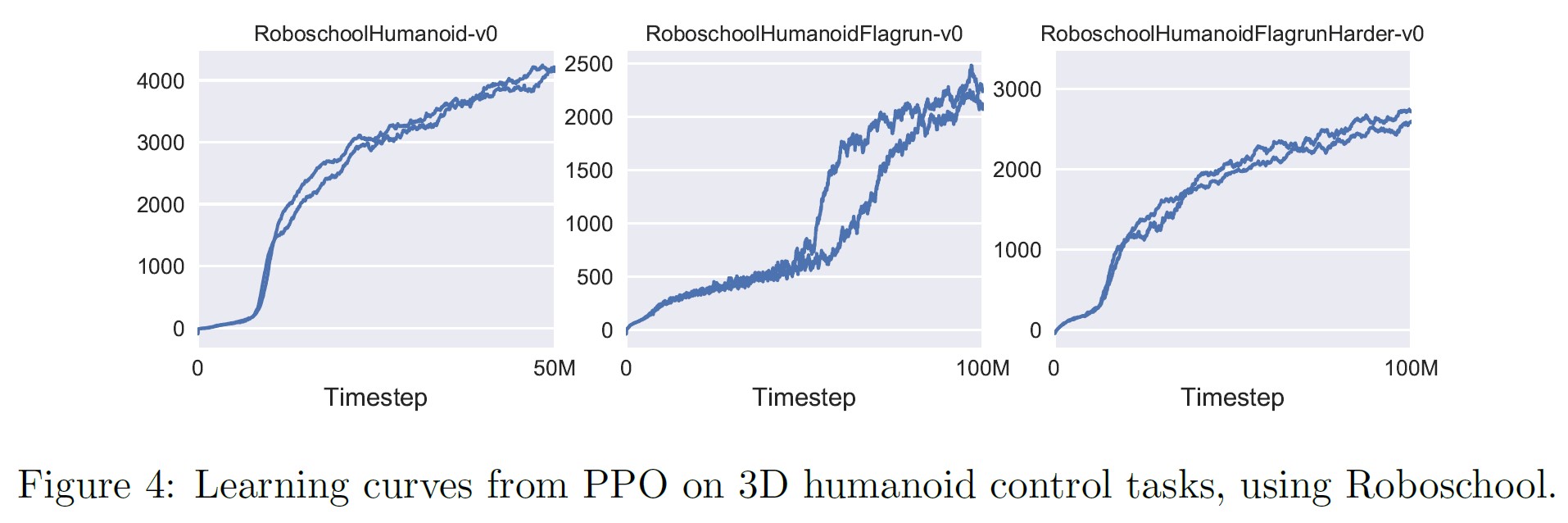
高次元の連続制御問題に対するPPOの性能を示すために，3Dヒューマノイドを含む一連の問題で訓練を行った．

ロボットは，キューブで殴られながら，ランニングしたり，ステアリングしたり，地面から立ち上がったりしなければならない．

（1）RoboschoolHumanoid：前進運動のみ，（2）RoboschoolHumanoidFlagrun：目標の位置を200タイムステップ毎または目標に到達する毎にランダムに変化させる，（3）RoboschoolHumanoid-FlagrunHarder：ロボットがキューブに襲われ，地面から起き上がらなければならない，の3つをテストしている．

3つのタスクの学習曲線は図4，学習した方策の静止画は図5を参照されたい．

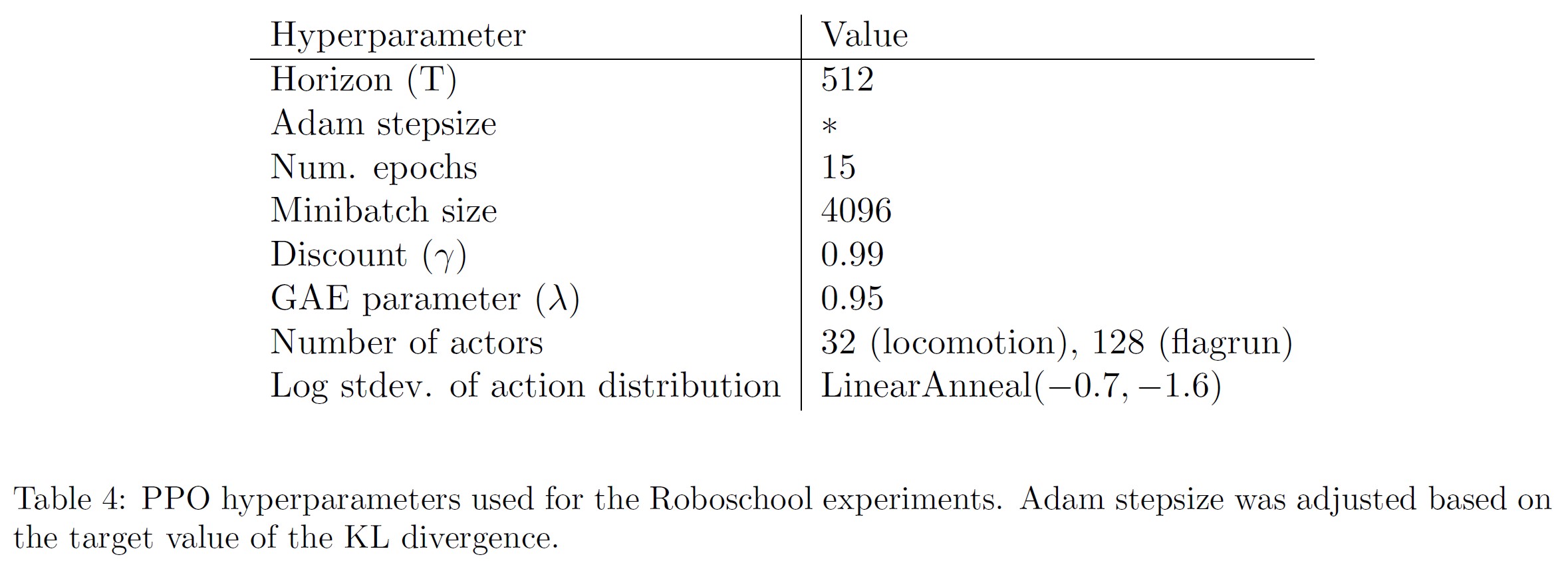
ハイパーパラメータは表4に示す通りである．

同時並行で，Heessら[Hee+17]はPPOの適応的KL variant（4章）を用いて3Dロボットのロコモーション方策を学習した．

6.4節：Comparison to Other Algorithms on the Atari Domain（Atariドメイン上の他のアルゴリズムとの比較）

また，Arcade Learning Environment[Bel+15]ベンチマークでPPOを実行し，A2C[Mni+16]とACER[Wan+16]のよくチューニングされた実装と比較した．

3つのアルゴリズムすべてにおいて，[Mni+16]で使用されたのと同じ方策のネットワークアーキテクチャを使用した．

PPOのハイパーパラメータは表5に示されている．

他の2つのアルゴリズムについては，このベンチマークで性能を最大化するようにチューニングされたハイパーパラメータを使用した．

全49ゲームの結果と学習曲線の表は付録Bに記載されている．

（1）訓練期間全体の1エピソードあたりの平均報酬（高速学習が有利），（2）直近の100訓練エピソードの1エピソードあたりの平均報酬（最終性能が有利），の2つのスコアリング指標を考慮した．

表2は，各アルゴリズムが「勝利」したゲーム数を示している．

ここでは，3回の試行でスコアリング指標を平均して勝利者を算出した．

7章：Conclusion（結論）

我々は，確率的勾配上昇の複数のエポックを用いて各方策の更新を行う方策最適化手法のファミリーである近傍方策最適化を導入した．

これらの手法は，信頼領域法の安定性と信頼性を持ちながら，バニラ方策勾配法の実装に対して数行のコード変更しか必要とせず，より一般的な設定（例えば，方策と価値関数のジョイントアーキテクチャを使用する場合）で適用でき，より優れた全体性能を持つ．

References（参考文献）

1. [Bel+15] M. Bellemare, Y. Naddaf, J. Veness, and M. Bowling. “The arcade learning environment: An evaluation platform for general agents”. In: Twenty-Fourth International Joint Conference on Artificial Intelligence. 2015.
2. [Bro+16] G. Brockman, V. Cheung, L. Pettersson, J. Schneider, J. Schulman, J. Tang, and W. Zaremba. “OpenAI Gym”. In: arXiv preprint arXiv:1606.01540 (2016).
3. [Dua+16] Y. Duan, X. Chen, R. Houthooft, J. Schulman, and P. Abbeel. “Benchmarking Deep Reinforcement Learning for Continuous Control”. In: arXiv preprint arXiv:1604.06778 (2016).
4. [Hee+17] N. Heess, S. Sriram, J. Lemmon, J. Merel, G. Wayne, Y. Tassa, T. Erez, Z. Wang, A. Eslami, M. Riedmiller, et al. “Emergence of Locomotion Behaviours in Rich Environments”. In: arXiv preprint arXiv:1707.02286 (2017).
5. [KL02] S. Kakade and J. Langford. “Approximately optimal approximate reinforcement learning”. In: ICML. Vol. 2. 2002, pp. 267–274.
6. [KB14] D. Kingma and J. Ba. “Adam: A method for stochastic optimization”. In: arXiv preprint arXiv:1412.6980 (2014).
7. [Mni+15] V. Mnih, K. Kavukcuoglu, D. Silver, A. A. Rusu, J. Veness, M. G. Bellemare, A. Graves, M. Riedmiller, A. K. Fidjeland, G. Ostrovski, et al. “Human-level control through deep reinforcement learning”. In: Nature 518.7540 (2015), pp. 529–533.
8. [Mni+16] V. Mnih, A. P. Badia, M. Mirza, A. Graves, T. P. Lillicrap, T. Harley, D. Silver, and K. Kavukcuoglu. “Asynchronous methods for deep reinforcement learning”. In: arXiv preprint arXiv:1602.01783 (2016).
9. [Sch+15a] J. Schulman, P. Moritz, S. Levine, M. Jordan, and P. Abbeel. “High-dimensional continuous control using generalized advantage estimation”. In: arXiv preprint arXiv:1506.02438 (2015).
10. [Sch+15b] J. Schulman, S. Levine, P. Moritz, M. I. Jordan, and P. Abbeel. “Trust region policy optimization”. In: CoRR, abs/1502.05477 (2015).
11. [SL06] I. Szita and A. L¨orincz. “Learning Tetris using the noisy cross-entropy method”. In: Neural computation 18.12 (2006), pp. 2936–2941.
12. [TET12] E. Todorov, T. Erez, and Y. Tassa. “MuJoCo: A physics engine for model-based control”. In: Intelligent Robots and Systems (IROS), 2012 IEEE/RSJ International Conference on. IEEE. 2012, pp. 5026–5033.
13. [Wan+16] Z. Wang, V. Bapst, N. Heess, V. Mnih, R. Munos, K. Kavukcuoglu, and N. de Freitas. “Sample Efficient Actor-Critic with Experience Replay”. In: arXiv preprint arXiv:1611.01224 (2016).
14. [Wil92] R. J. Williams. “Simple statistical gradient-following algorithms for connectionist reinforcement learning”. In: Machine learning 8.3-4 (1992), pp. 229–256.

付録A：Hyperparameters（ハイパーパラメータ）

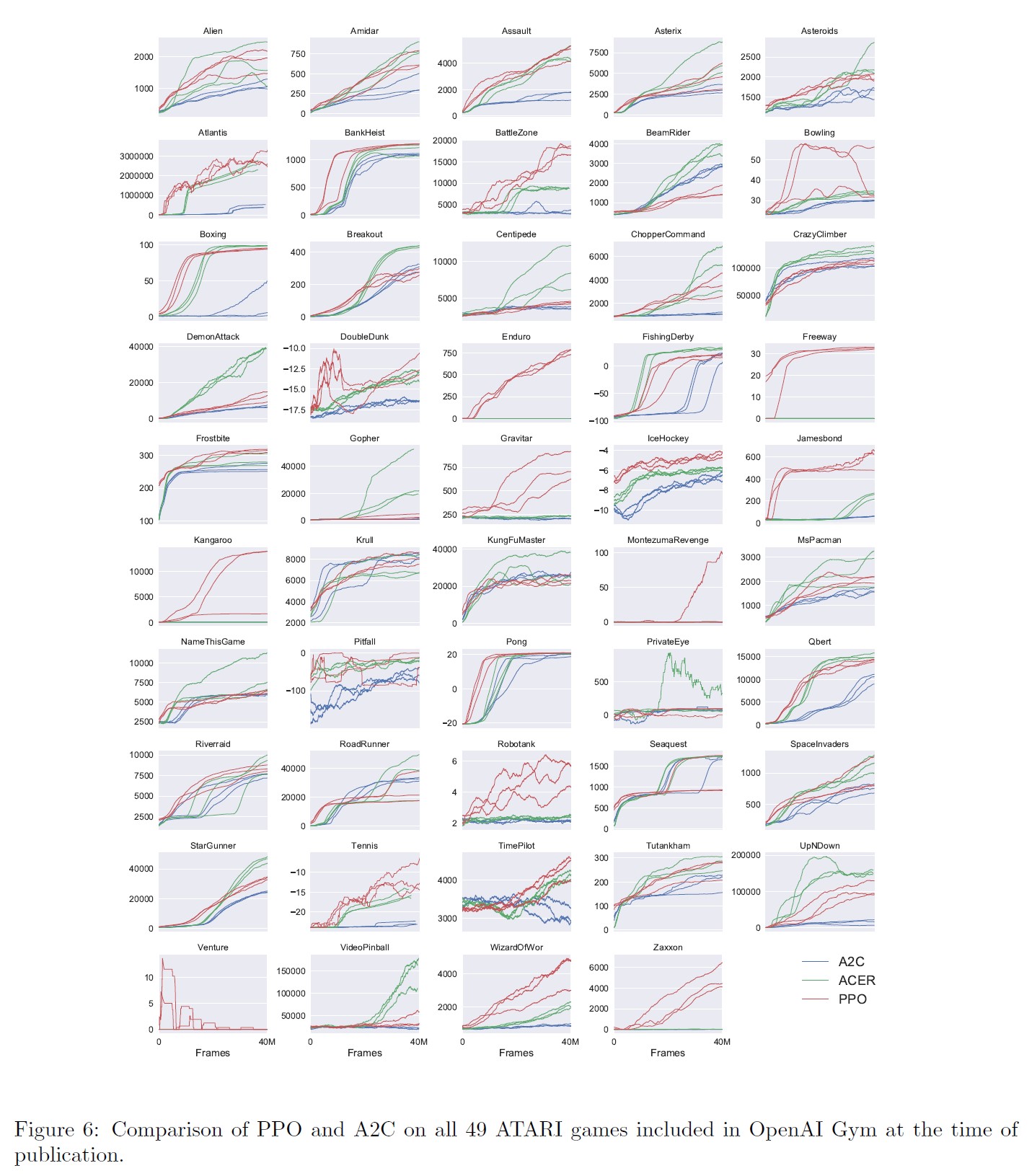
付録B：Performance on More Atari Games（その他のアタリゲームの性能）

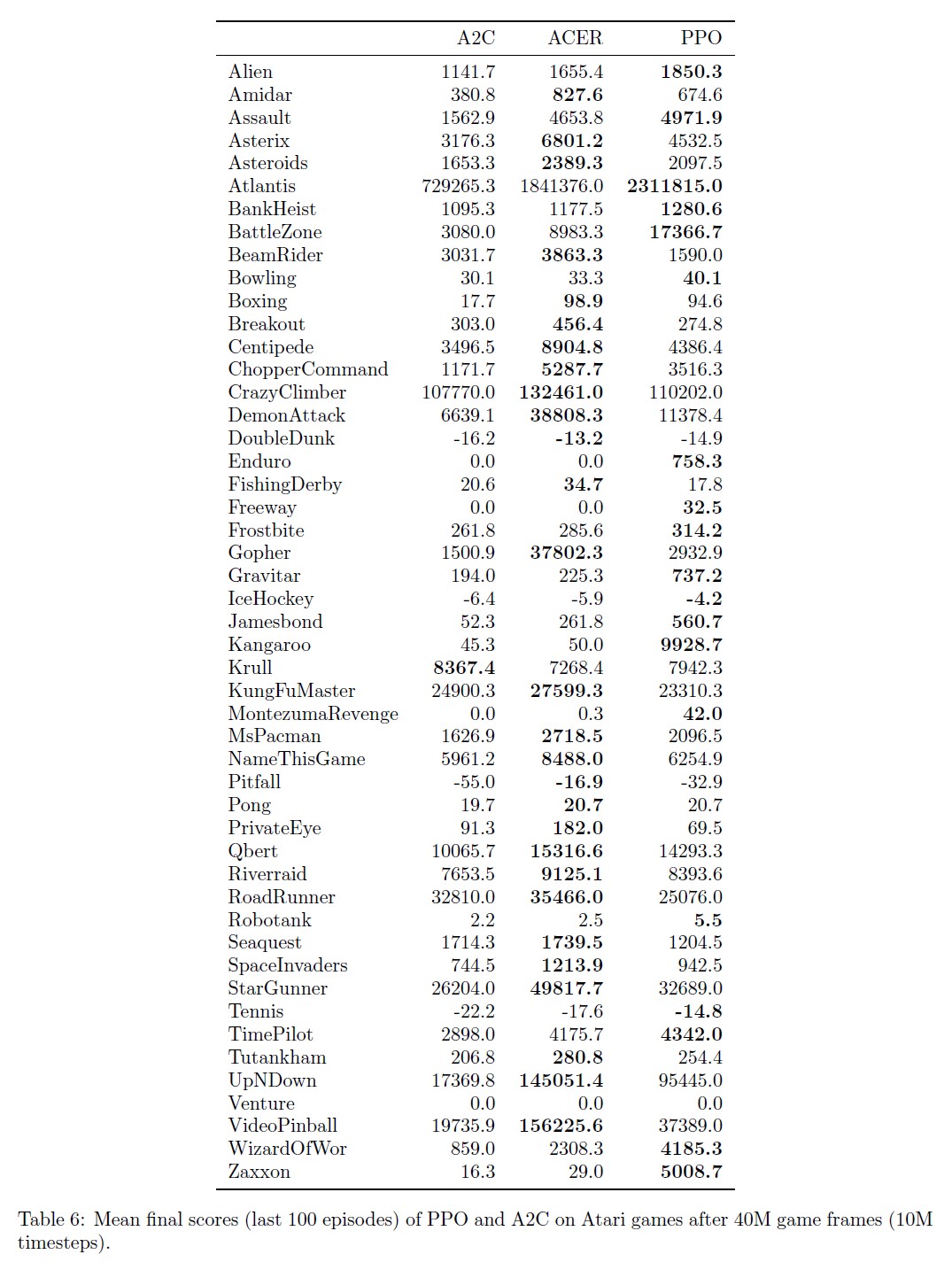
ここでは，より大規模な49のAtariゲームコレクションにおけるA2Cに対するPPOの比較を掲載する．

図6は3つのランダムシードのそれぞれの学習曲線を示し，表6は平均性能を示している．

参考：Proximal Policy Optimization Algorithmsの解説動画

Proximal Policy Optimization Algorithmsの解説動画です．

まとめ

Proximal Policy Optimization Algorithmsの日本語訳を紹介しました．

OpenAIの近傍方策最適化（PPO：Proximal Policy Optimization）がわかりました．

AIのプログラミング言語「C++/Python言語」を学べるおすすめのWebサイトを知りたいあなたはこちらからどうぞ．

独学が難しいあなたは，AIを学べるオンラインプログラミングスクール3社で自分に合うスクールを見つけましょう．後悔はさせません！

国内・海外のAIエンジニアのおすすめ求人サイトを知りたいあなたはこちらからどうぞ．

国内・海外のプロンプトエンジニアのおすすめ求人サイトを知りたいあなたはこちらからどうぞ．