【日本語訳】The Curse of Recursion: Training on Generated Data Makes Models Forget【モデル崩壊，再帰の呪い】

こういった悩みにお答えします．

こういった私から学べます．

AIのプログラミング言語「C++/Python言語」を学べるおすすめのWebサイトを知りたいあなたはこちらからどうぞ．

独学が難しいあなたは，AIを学べるオンラインプログラミングスクール3社で自分に合うスクールを見つけましょう．後悔はさせません！

国内・海外のAIエンジニアのおすすめ求人サイトを知りたいあなたはこちらからどうぞ．

国内・海外のプロンプトエンジニアのおすすめ求人サイトを知りたいあなたはこちらからどうぞ．

The Curse of Recursion: Training on Generated Data Makes Models Forgetの日本語訳を紹介します．

大規模言語モデルのモデル崩壊と再帰の呪いがわかります．

※図表を含む論文の著作権はThe Curse of Recursion: Training on Generated Data Makes Models Forgetの著者に帰属します．

The Curse of Recursion: Training on Generated Data Makes Models Forgetの目次は以下になります．

• Abstract
• 1章：Introduction
• 2章：Related Work
• 3章：What is Model Collapse?
• 4章：Theoretical intuition
• 5章：Evaluation
• 6章：Discussion and Conclusion
• Acknowledgements
• References
• 付録A：Appendix

The Curse of Recursion: Training on Generated Data Makes Models Forgetを解説しつつ，私の考えも語ります．

The Curse of Recursion: Training on Generated Data Makes Models Forgetの概要と私の日本語訳は以下になります．

Stable Diffusion revolutionised image creation from descriptive text.
Stable Diffusionは，説明的なテキストからの画像作成に革命をもたらした．

GPT-2, GPT-3(.5) and GPT-4 demonstrated astonishing performance across a variety of language tasks.
GPT-2，GPT-3（.5），GPT-4は，様々な言語タスクで驚異的な性能を発揮した．

ChatGPT introduced such language models to the general public.
ChatGPTは，このような言語モデルを一般に紹介した．

It is now clear that large language models (LLMs) are here to stay, and will bring about drastic change in the whole ecosystem of online text and images.
現在，大規模言語モデル（LLMs：Large Language Models）は，オンラインテキストと画像のエコシステム全体に劇的な変化をもたらすであろうことは明らかである．

In this paper we consider what the future might hold.
この論文では，未来がどうなるかを考える．

What will happen to GPT-{n} once LLMs contribute much of the language found online?
LLMがオンライン上の言語の多くを占めるようになったら，GPT-{n}はどうなるのだろうか?

We find that use of model-generated content in training causes irreversible defects in the resulting models, where tails of the original content distribution disappear.
我々は，モデルによって生成されたコンテンツを訓練に使用すると，結果として得られるモデルに不可逆的な欠陥が生じ，オリジナルのコンテンツ分布のテールが消えてしまうことを発見した．

We refer to this effect as Model Collapse and show that it can occur in Variational Autoencoders, Gaussian Mixture Models and LLMs.
この効果を「Model Collapse」（モデル崩壊）と呼び，変分オートエンコーダ，ガウス混合モデル，LLMで発生する可能性があることを示す．
※この名前は，Generative Adversarial Networks（GAN）の「モード崩壊」に関する文献からヒントを得たもので，GANはすべての識別器を騙す限られた出力セットを生成し始める．モデル崩壊とは，モデルが最終的にGANのモード崩壊と同様の状態に収束するプロセスである．本論文の原文では，この効果を「モデル認知症」と呼んでいたが，「認知症」という医学的概念を矮小化し，不快感を与える可能性があるというフィードバックを受けて，これを変更することにした．

We build theoretical intuition behind the phenomenon and portray its ubiquity amongst all learned generative models.
この現象の背後にある理論的直観を構築し，学習済みのすべての生成モデルにおけるそのユビキタス性を描写する．

We demonstrate that it has to be taken seriously if we are to sustain the benefits of training from large-scale data scraped from the web.
また，ウェブから収集した大規模データから訓練することの利点を維持するためには，この現象を真剣に考慮する必要があることを実証する．

Indeed, the value of data collected about genuine human interactions with systems will be increasingly valuable in the presence of content generated by LLMs in data crawled from the Internet.
実際，インターネットからクロールされたデータの中にLLMによって生成されたコンテンツが存在する場合，システムと人間の真のインタラクションについて収集されたデータの価値はますます高くなるであろう．

https://arxiv.org/abs/2305.17493

私の日本語訳の注意点は以下になります．

• 概要は英語と日本語を両方掲載しましたが，本文は私の日本語訳のみを掲載していること（英語で読みたいあなたは原文を読みましょう！）
• 基本的には原文の直訳ですが，わかりにくい箇所は意訳や説明を追加している箇所があること
• 原文の「Acknowledgements」（謝辞）は省略していること
• 本文中に登場する表記「[Solaiman et al., 2019]」などは参考文献ですので，興味がある方は本記事の参考文献を参照されたいこと

それでは，The Curse of Recursion: Training on Generated Data Makes Models Forgetの本文を読みすすめましょう！

1章：Introduction（はじめに）

人間のコミュニケーションの多くは，オンラインで行われている．

毎日，何十億通もの電子メール，何十億通ものソーシャルメディア，何百万ものニュース記事が交わされている．

しかし，今世紀に入ってからは，検索エンジンが検索対象を決定するようになり，過去10年間では，スペルや文法を修正できるスマートなテキストエディタが，我々が作成するテキストに手を加えるのに役立っている．

今や，テキストは効率的に編集・分析できるようになっただけでなく，大規模な言語モデル（LLMs：Large Language Models）により，大量に生成することもできるようになった．

これらのモデルは現在，その出力が人間が書いたテキストと確実に区別できないという意味で，チューリングテストの弱い形式を（議論の余地なく）パスしている[Solaiman et al., 2019]．

LLMの開発は非常に複雑で，大量の訓練データを必要とする．

最近の強力なモデルの中には，インターネットの多くのスクレイピングを使用して訓練し，さらに人間のフィードバックからの強化学習（RLHF：Reinforcement Learning from Human Feedback）でファインチューニングしているという逸話がある[Griffith et al., 2013, OpenAI, 2023]．

これにより，有効なデータセットサイズがさらに拡大される．

しかし，GPT-4を含む現在のLLM[Devlin et al., 2018, Liu et al., 2019, Brown et al., 2020, Zhang et al., 2022]は，主に人間が作成したテキストで訓練されていたが，これは将来的に変化する可能性がある．

将来のモデルの訓練データもほとんどがウェブからのスクレイピングであれば，必然的に前任者が作成したデータで訓練するようになる．

この論文では，例えばGPTのバージョンによって生成されたテキストが，後続モデルの訓練データセットの大半を占めるようになった場合に何が起こるかを調査する．

GPTのバージョンGPT-{n}は生成nが増加するとどうなるのか?

※これは，テキストモデルに限ったことではない．人間の作曲家が作り，人間の音楽家が演奏した音楽が，モデルを訓練し，その出力が他のモデルを訓練した場合，どうなるかということも考えることができる．

他のモデルが作成したデータから学習することで，モデル崩壊が起こることを発見した．

モデル崩壊とは，時間経過に伴うデータ分布の変化がない場合でも，時間が経つにつれてモデルが真の基礎データ分布を忘れてしまうという退行過程である．

ガウス混合モデル（GMMs：Gaussian Mixture Models），変分オートエンコーダ（VAE：Variational AutoEncoders），大規模言語モデル（LLMs：Large Language Models）のモデル崩壊の例を挙げる．

時間の経過とともに，真の分布に関する情報が失われ始め，最初は尾が消えることから始まり，何生成にもわたって学習された動作が，非常に小さな分散を持つ点推定値に収束し始めることを示す．

さらに，このプロセスは，関数推定誤差がないなど，長期学習にとってほぼ理想的な条件の場合であっても，不可避であることを示す．

※訳注：原文では図1を参照していませんが，こちらに記載しておきます．

最後に，モデル崩壊のより広い意味について議論する．

オリジナルのデータ分布にアクセスすることが重要であることに注意されたい．

基礎分布のテールが問題となる学習では，人間が作成した実際のデータにアクセスする必要がある．

言い換えれば，インターネット上でコンテンツを公開するためにLLMを大規模に使用することは，彼らを訓練するためのデータ収集を汚染することになる．

LLMと人間とのインタラクションに関するデータは，ますます貴重なものとなるだろう．

本論文は以下のような構成になっている．

まず，3章と4章では，モデル崩壊が起こる理由を説明する．

直感を最もよく表現するために，サンプリングによる誤差が必然的にモデル崩壊を引き起こす1次元ガウスの簡単な例を示し，それをいくつかの仮定の下で多次元生成モデルへと拡張する．

両モデルとも，真の分布からのWasserstein距離で定義されるリスクについて，同様の下界が導出される．

次に，GMMとVAEに着目し，関数近似誤差がモデル崩壊をさらに悪化させることを示す．

最後に，最もよく使われる言語モデルのファインチューニングの設定について説明し，モデルがゼロから訓練されるのとは対照的に，モデル崩壊の初期兆候のみが検出されることを報告する．

本論文では，以下のような貢献をしている．

• 学習における退行過程の存在を示し，それをモデル崩壊と名付けた．
• モデル崩壊が様々な種類のモデルやデータセットに存在することを実証している．
• モデル崩壊を避けるためには，人間が作成した本物のコンテンツにアクセスすることが不可欠であることを示す．

2章：Related Work（関連研究）

本章では，既存の文献からモデル崩壊に最も近い2つの概念である「破滅的忘却」と「データポイズニング」を取り上げることにする．

どちらも設定が根本的に異なるため，モデル崩壊の現象を完全に説明することはできないが，観察された現象に別の視点を与えてくれる．

2.1節：Continual learning and catastrophic forgetting（継続学習と破滅的忘却）

静的なデータ分布から学習しようとする従来の機械学習とは異なり，継続学習はデータが逐次的に供給される動的なものから学習しようとする[Van de Ven and Tolias, 2019]．

これは，タスクベースで，タスクの境界が区切られたデータが提供される傾向がある．

例えば，犬を猫から分類する，手書きの数字を認識する，などである．

我々の仕事は，タスクフリーの継続学習[Aljundi et al., 2019]に似ており，個別のタスクの概念なしにデータ分布が徐々に変化する．

我々の仕事は，変化したデータ分布が，前の反復における訓練の結果として，モデル自身から生じるという特定のシナリオを検討するものである．

継続学習における典型的な挑戦は，新しい情報を学習する際にモデルが以前のサンプルを忘れてしまうことであり，これは破滅的忘却[Kirkpatrick et al., 2017]として知られている．

これを防ぐ典型的な方法は，正則化（Memory Aware Synpass[Aljundi et al., 2018]）を使用するか，あるいは単にデータに依存する（例：Learning without Forgetting[Li and Hoiem, 2017]）ことです．

これは我々の仕事と間接的なつながりがあるが，モデル崩壊の過程におけるデータは異なる生成モデルによって作られるため，異なっている．

2.2節：Data poisoning（データポイズニング）

ポイズニング攻撃は，デプロイ時にモデルのパフォーマンスを低下させるために，訓練中に細工して挿入される[Biggio et al., 2012]．

悪意のあるデータを訓練データに挿入することで，特別なトリガーで起動できる意図しない動作を誘発することができる[Gu et al., 2017]．

データポイズニングに関する初期の文献は，主にラベル付きサンプルで分類器を学習させる教師あり学習に焦点を当てていた．

しかし，対比学習（対照学習）[Radford et al., 2021]とLLM[Brown et al., 2020]の出現により，より最近のモデルは大規模なウェブクロールで訓練され，これらの信頼できないウェブソースでデータポイズニング攻撃がより実現可能になった．

最近の研究では，サンプルのごく一部に悪意のあるデータを導入することで，ウェブスケールのデータセットが汚染されることが実証されている[Carlini and Terzis, 2021, Carlini et al., 2023]．

3章：What is Model Collapse?（モデル崩壊とは?）

定義3.1（モデル崩壊）：モデル崩壊とは，学習した生成モデルに影響を与える退行過程であり，生成されたデータが次の生成モデルの訓練セットを汚染することになる．汚染されたデータで訓練されたモデルは，現実を誤認してしまう．早期モデル崩壊と晩期モデル崩壊という2つの特殊なケースに分ける．早期モデル崩壊では，モデルは分布のテールに関する情報を失い始める．晩期モデル崩壊では，モデルはオリジナルの分布の異なるモードを絡め取り，オリジナルの分布とはほとんど似ていない，しばしば非常に小さな分散を持つ分布に収束してしまう．

なお，この過程は，時間をかけて複数のモデルを考えるという点で，破滅的忘却の過程とは異なる．

この場合，モデルは以前に学習したデータを忘れるのではなく，自分の信念を強化することによって，現実と信じているものを誤って解釈し始める．

このプロセスは，2つの特定のエラー源が生成を超えて複合的に作用し，オリジナルのモデルから逸脱することで発生する．

このうち，1つの誤差が主要な役割を果たしており，この誤差がなければ，このプロセスは最初の生成を超えて発生することはない．

※訳注：原文では図2を参照していませんが，こちらに記載しておきます．

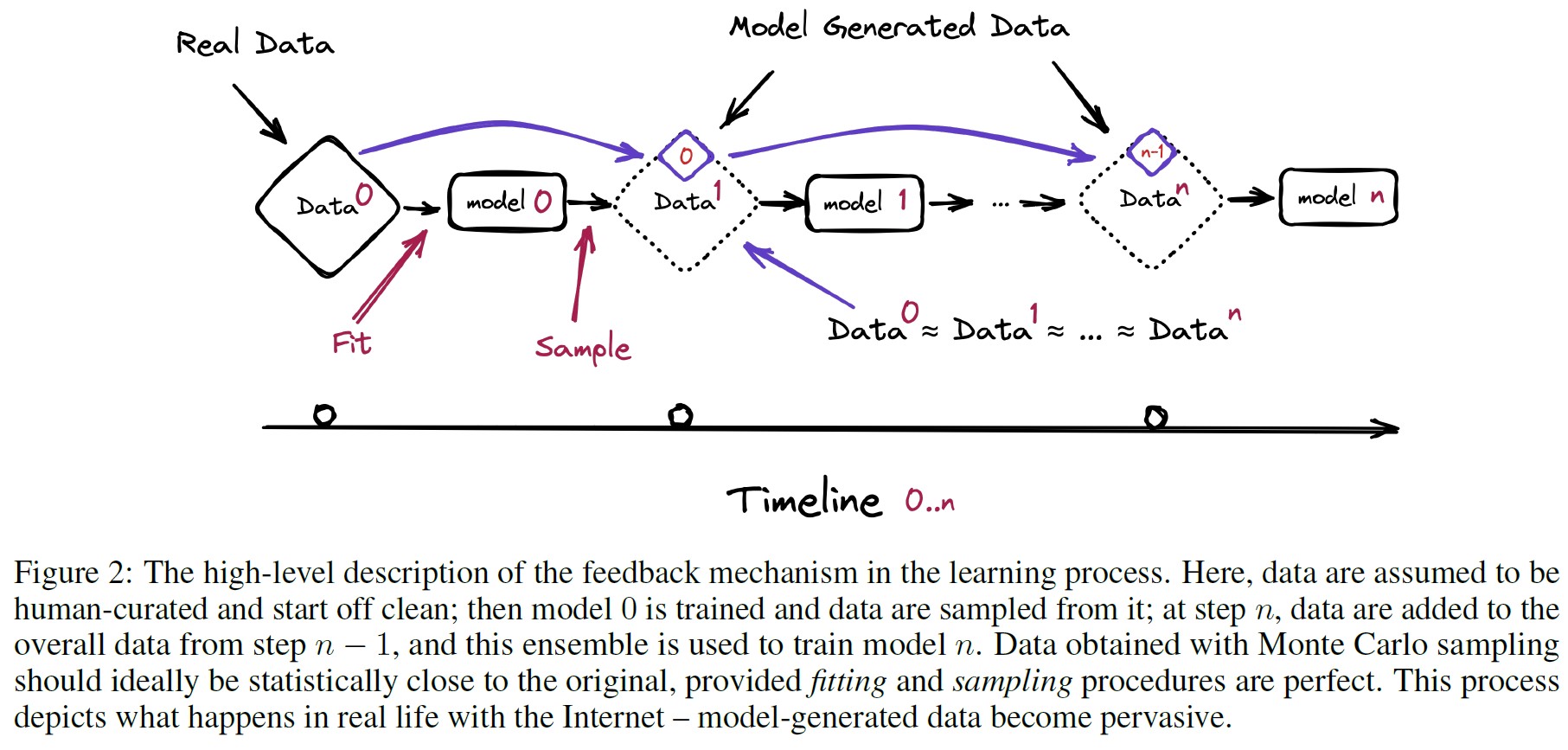
3.1節：Causes of model collapse（モデル崩壊の原因）

モデル崩壊の主な原因は2つあり，1つは一次的なもの，もう1つは二次的なもので，今から説明する．

4章では，これらがどのようにして観測された誤差を生じさせるのか，異なる原因がどのように複合化するのか，平均的なモデルの発散率をどのように定量化できるのかについて，さらに数学的な直観を提供する．

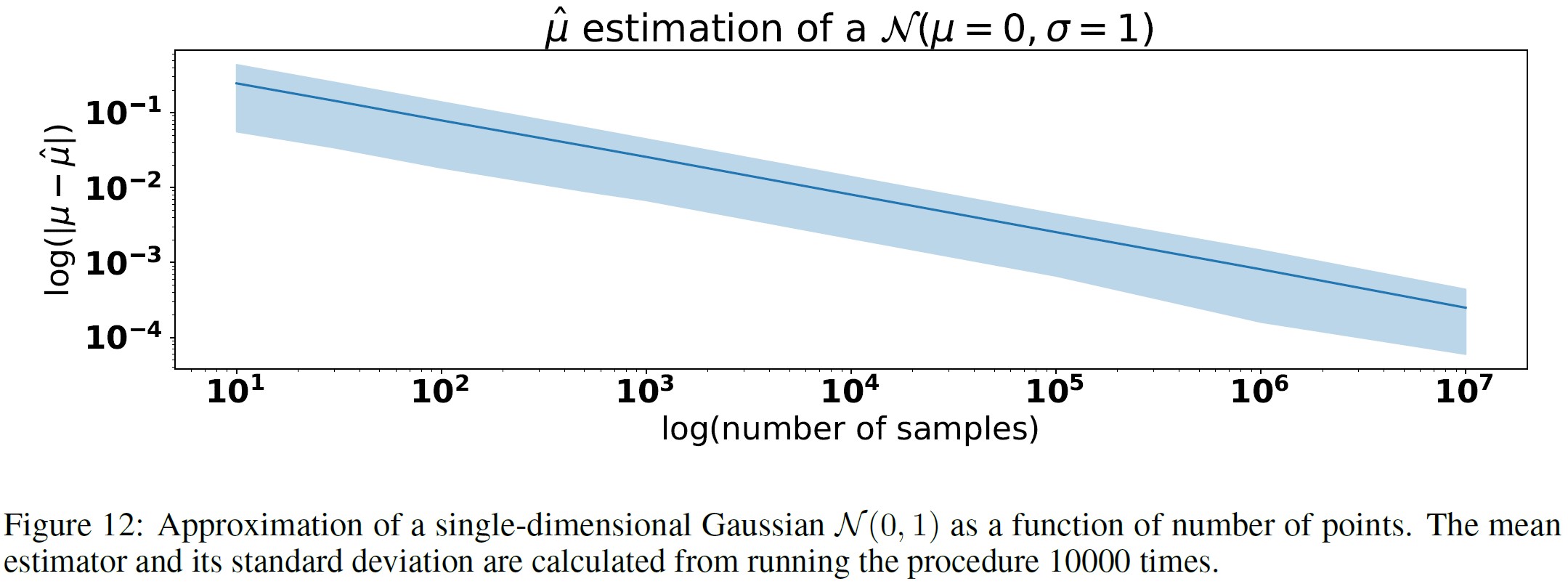
• Statistical Approximation Error（統計近似誤差）：サンプルの数が有限であるために発生し，サンプルの数が無限大になるにつれて消失する，主要なタイプの誤差である．これは，再サンプリングの各段階で情報が失われる可能性がゼロでないために発生する．図12は，近似誤差の一例を示す．ここでは，有限個のサンプルから1次元ガウスを近似している．非常に多くの点を使用しているにもかかわらず，誤差は大きく，\(10^7\)個のサンプルで平均を0.00024899±1.89382984\(e^{-4}\)と推定し，真の値は0であることがわかる．
• Functional Approximation Error（関数近似誤差）：これは二次的な誤差で，関数近似の表現が不十分であることに起因する（あるいは，オリジナルの分布支持の外側で表現が強すぎる場合もある[Nguyen et al., 2015]）．ニューラルネットワークが極限において普遍的な関数近似器であることはよく知られているが，実際にはこれが常に正しいとは限らない．特に，ニューラルネットワークは，オリジナルの分布のサポートの外側に非ゼロの尤度を導入することができる．この誤差の簡単な例は，2つのガウシアンの混合物を1つのガウシアンでフィッティングしようとする場合である．データ分布について完璧な情報を持っていたとしても，モデルの誤差は避けられない．また，統計誤差がない場合，関数近似誤差は最初の生成でのみ発生することに注意することが重要である．新しい分布が関数近似のイメージに属すると，生成を超えた全く同じ分布が維持される．

上記のそれぞれは，モデル崩壊を悪化させたり，良くしたりする原因となる．

近似力の向上は，諸刃の剣となる可能性がある．

より優れた表現力は，統計的なノイズを打ち消し，真の分布の良い近似をもたらすかもしれないが，同様にこのノイズを増幅させる可能性がある．

多くの場合，個々の不正確さが組み合わさって全体の誤差を拡大させるというカスケード効果が発生する．

密度モデルをオーバーフィットさせると，モデルの外挿が不正確になり，訓練セットのサポートでカバーされていない低密度の領域にも高い密度を与える可能性がある．

このような領域は，任意の頻度でサンプリングされることになる．

現代のコンピュータには，浮動小数点数の表現方法から来る更なる計算誤差があることも特筆すべき点である．

この誤差は，異なる浮動小数点数の範囲に均等に広がっていないため，与えられた数値の正確な値を推定することが難しくなっている．

このような誤差は大きさが小さく，より精密なハードウェアで修正可能であるため，モデル崩壊への影響は小さくなる．

4章：Theoretical intuition（理論的直感）

本章では，モデル崩壊現象の理論的な直観を提供することを目的とする．

モデル崩壊のプロセスは，前の生成が作ったデータに対して再帰的に訓練する生成モデルにおいて普遍的であることを主張する．

我々は，おもちゃの数学モデルを構築し，興味のある量の解析式を提供するのに十分なほど単純であることを証明するとともに，モデル崩壊の現象を描写する．

我々は，様々な誤差の原因が，オリジナルの分布の最終的な近似にどのような影響を与えるかを定量化することを目的としている．

3.1節で説明したように，我々が関心を持つ主な原因は，統計誤差と関数誤差の2つである．

現実の世界では無限にサンプルがあることは稀なので，関数近似誤差を定量化するだけでは，モデル崩壊の議論にはあまり意味がない．

そこで，関数近似誤差がない場合の離散分布と，関数近似誤差が統計誤差とどのように複合化するかを示す1次元ガウスの場合の2つの簡単なケースを検討する．

これから考える全体的な確率過程（これを生成データによる学習と呼ぶ）は次のようなものである．

第i生成において，i.i.d.（独立同分布）確率変数\(X_j^i\)からなるデータセット\(\mathcal{D}_i\)があると仮定する．

ここで，\(j \in \{1, …, M_i \}\)はi生成での標本数を表し，\(M_i \geq 2\)である．

\(X^i\)の分布を\(p_i\)とする．

ここで\(p_0\)は，データの元となるオリジナルの分布を表すと仮定する．

第i生成から第i+1生成に行くとき，我々は近似\(p_{\theta_{i+1}}\)で，\(\mathcal{D}_i\)のサンプルの分布を推定することを目指す．

このステップは，我々が関数近似\(\mathcal{F}_\theta : p_i \rightarrow p_{\theta_{i+1}}\)と呼ぶものである．

次に，非負のパラメータ\(\alpha_i\)，\(\beta_i\)，\(\gamma_i\)の合計が1になる分布\(p_{i+1} = \alpha_i p_{\theta_{i+1}} + \beta_i p_i + \gamma_i p_0\)からデータセット\(\mathcal{D}_{i+1}\)を再サンプルする．

これらは，異なる生成のデータの使用比率を表している．

これは，オリジナルの分布に由来するデータ（\(\gamma_i\)），前の生成で使用されたデータ（\(\beta_i\)），新しいモデルで生成されたデータ（\(\alpha_i\)）の混合に相当する．

これをサンプリングステップと呼ぶ．

この後の数学的モデルでは，\(\alpha_i = \gamma_i = 0\)，つまり1つのステップからのデータのみを使用することを考慮する一方，数値実験はより現実的なパラメータの選択で実施する．

4.1節：Discrete distributions with exact approximation（厳密な近似を用いた離散分布）

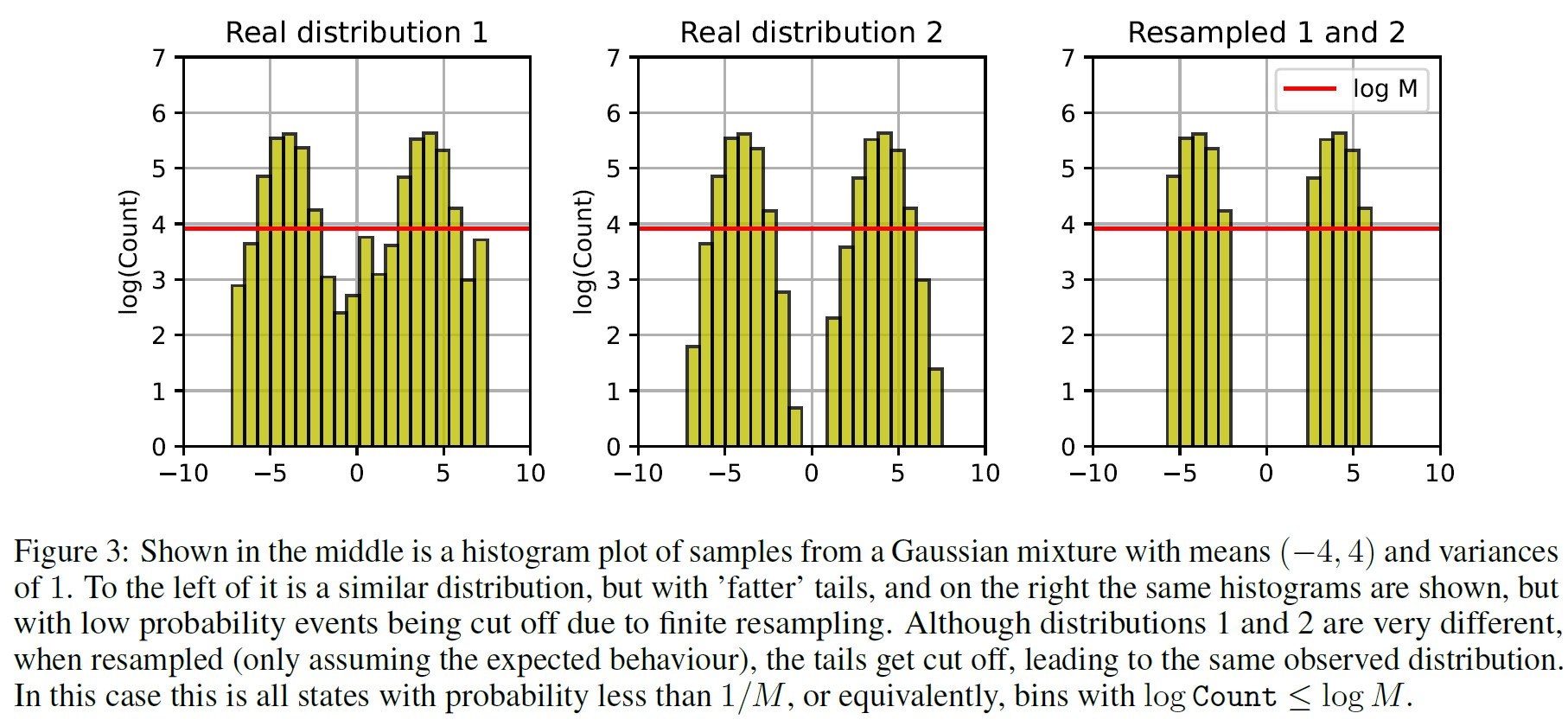
この節では，例えば図3に示すようなヒストグラムで表される離散確率分布を考える．

以下では，関数近似誤差がない場合，すなわち\(\mathcal{F}(p)=p\)の場合の確率過程を考える．

この場合，モデル崩壊はサンプリングステップによる統計誤差によってのみ発生する．

最初は，テール（低確率事象）がサンプリングされる確率が低いために消え始め，時間の経過とともに分布はデルタ関数になる．

サンプルサイズをMとすると，状態iを確率\(q \leq \frac{1}{M}\)で考えると，それらのイベントから来る値iを持つサンプルの期待数は1より少なくなり，実際にはそれらの情報を失うことになる．

これは図3に描かれているように，頻度の低いイベントはカットされる．

より一般的に，ある状態iを確率qで考えると，標準的な条件付き確率を用いれば，情報を失う（ある生成でデータをサンプリングしない）確率は1-qに等しいことを示すことができる．

しかし，これは，ある状態に位置するデルタ関数に収束しなければならないことを意味し，ある状態に行き着く確率は，オリジナルの分布からその状態をサンプリングする確率に等しい．

しかし，この過程が分布をデルタ関数に変えることを直接示すにはどうすればいいのだろうか?

\(\mathbf{X}^i \rightarrow \mathcal{F}_\theta \rightarrow p_{i+1} \rightarrow \mathbf{X}^{i+1}\)という過程を考えると，\(\mathbf{X}^{i+1}\)は\(\mathbf{X}^i\)にのみ依存するので，これはマルコフ連鎖を形成することがわかる．

さらに，もしすべての\(X_j^i\)が同じ値であれば，次の生成では近似された分布はまさにデルタ関数となり，したがって\(X_j^{i+1}\)もすべて同じ値になる．

これはマルコフ連鎖が少なくとも1つの吸収状態を含むことを意味し，したがって確率1で吸収状態の1つに収束する．

これはよく知られた事実であり，その証明は付録A.1にある．

この連鎖では，吸収状態はデルタ関数に対応するものだけである．

その結果，モデル崩壊の進行に従うと，連鎖が吸収されたときにオリジナルの分布の情報をすべて失って，一定の状態に行き着くことが保証される．

※浮動小数点表現が離散的であるため，モデルのパラメータに対するマルコフ連鎖が離散的となり，この議論は一般的にも有効である．したがって，モデルのパラメタリゼーションがデルタ関数を許容する限り，サンプリング誤差のために，吸収可能な状態はデルタ関数だけであるため，我々はデルタ関数に到達することになる．

以上の議論から，完全な関数近似を持つ離散分布の場合，早期段階と晩期段階の両方のモデル崩壊が生じなければならないことがわかる．

4.2節：Single dimensional Gaussian（1次元ガウシアン）

離散分布に関する議論に続いて，関数近似誤差とサンプリング誤差の両方が，モデル崩壊のプロセスをどのように複雑化（または相殺）させるかを考察する．

これを実証するために，1次元のガウス\(X^0 \sim \mathcal{N}(\mu, \sigma^2)\)を考える．

我々が観測したデータを完全に信頼している場合，関数近似は標本平均と分散を推定し，1次元ガウシアンにフィッティングすることを含む．

不偏標本平均推定量と分散推定量を用いてそれらを推定することができる．

$$ \mu_{i+1} = \frac{1}{M_i} \sum_j X_j^i; \ \ \ \sigma_{i+1}^2 = \frac{1}{M_i - 1} \sum_j (X_j^i - \mu_{i+1})^2 \tag{1} $$

ここで，もし最尤推定を使うとすれば，代わりに偏った分散推定量になることに注意されたい．

これらの推定値では，関数近似のステップは，単にこれらのパラメータを持つ正規分布を考えることに対応し，そこからサンプリングすることができる．

$$ X_j^{i+1} | \mu_{i+1}, \sigma_{i+1} \sim \mathcal{N} (\mu_{i+1}, \sigma_{i+1}^2) $$

これにより，\(X_j^i\)の条件付き分布が得られ，\(X_j^i\)の完全な分布を計算することができる．

式2から，最初の近似の後でも，\(X_j^i\)の分布はもはや正規分布ではなく，分散ガンマ分布[Fischer et al., 2023]に従うことがわかる．

しかし，各生成での確率密度関数を書く代わりに，独立な確率変数で明示的に構成することができる．

特に，\(\mu_1\)と\(\sigma_1\)は独立であり，\(\mu_1 \sim \mathcal{N}(μ, \frac{\sigma^2}{M_0})\)と\((M_0 - 1) \sigma_1^2 \sim \sigma^2 \Gamma (\frac{M_0 - 1}{2}, \frac{1}{2})\)であることはよく知られている[Cochran, 1934]．

以下では，\(\mathcal{N}(0, 1)\)で分布する確率変数をZ，\(\frac{1}{M_{i-1}-1} \Gamma (\frac{M_{i-1}-1}{2}, \frac{1}{2})\)で分布する確率変数を\(S^i\)とする．

\begin{eqnarray}
X_j^0 &=& \mu + \sigma Z_j^0; \ \ \ X_j^1 = \mu + \frac{\sigma}{\sqrt{M_0}} Z^1 + \sigma \sqrt{S^1} Z_j^1; ... \tag{2} \\
X_j^n &=& \mu + \frac{\sigma}{\sqrt{M^0}} Z^1 + \frac{\sigma}{\sqrt{M^1}} \sqrt{S^1} Z^2 + ... \\
&&+ \frac{\sigma}{\sqrt{M_{n-1}}} \sqrt{S^1 * ... * S^{n-1}} Z^n + \sigma \sqrt{S^1 * ... * S^n} Z_j^n
\end{eqnarray}

\(Z^n\)と\(S^n\)は\(Z_j^{n-1}\)に直接依存するため，これらは共同分布ではないが，\(X_j^n\)を単独で考える場合，上式は完全な分布に関するすべての情報を提供する．

最初に計算しようとするのは分散である．

その正確な値を求めることは可能だが，ガンマ分布の平方根の平均と分散はガンマ関数で表現されるため，結果がかなり不便になる．

以下では，各標本サイズが大きいと仮定して，(\(1/M_i\))の各々ですべてを2次まで展開する（実際には，これは\(M \sim 100\)（訳注：iが100）を超えるとかなり正確になる）．

そうすると下式がわかる．

$$ \frac{1}{\sigma^2} Var(X_j^n) = \frac{1}{M_0} + \frac{1}{M_1} + ... + \frac{1}{M_{n-1}} + 1 + \mathcal{O}(2) $$

また，\(M_i=M\)が一定であると仮定すると，下式のようになる．

$$ Var(X_j^n) = \sigma^2 \left(1 + \frac{n}{M} \right); \ \ \ \mathbb{E}(X_j^n) = \mu $$

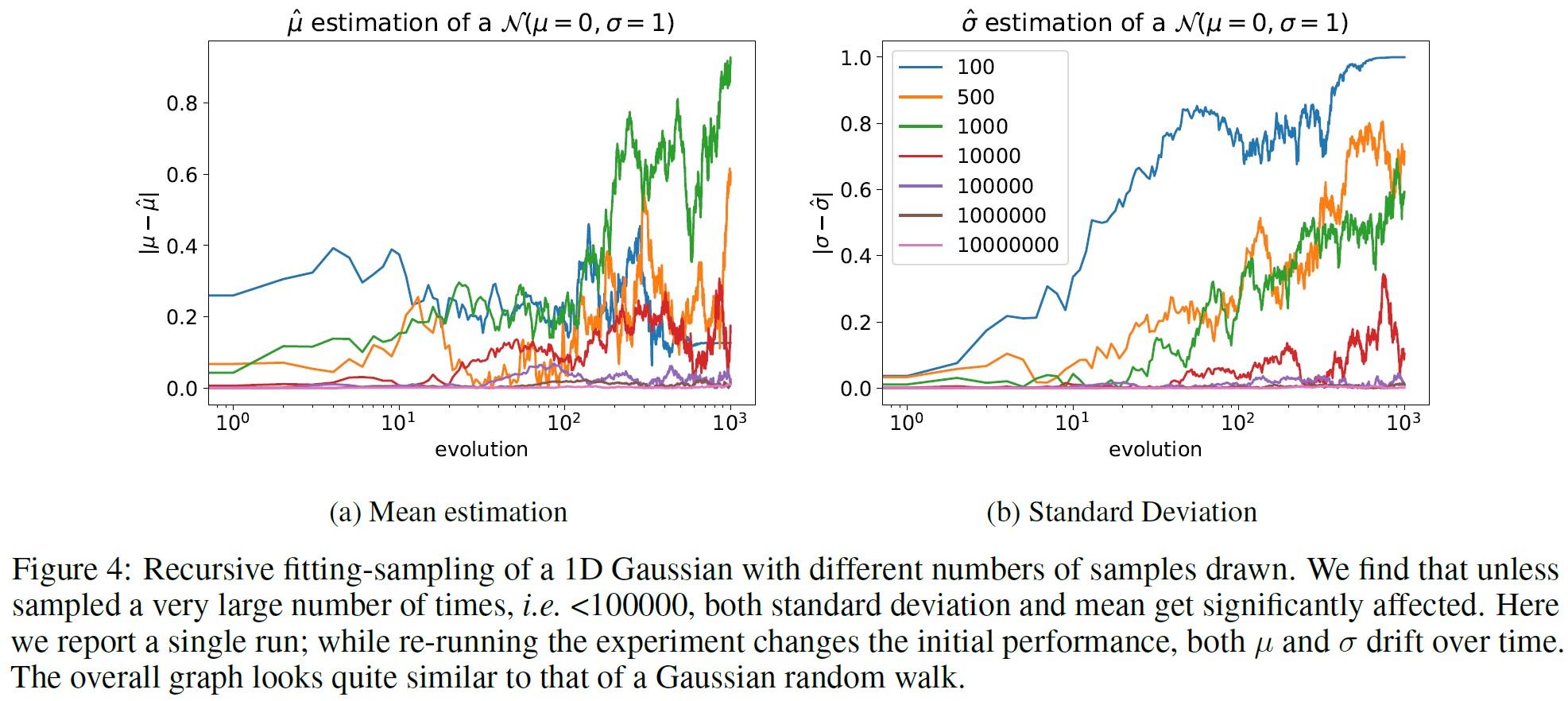
これは，\(n \rightarrow \infty\)として，分散が線形に発散することを意味する．

これは，1次元ガウシアンランダムウォークと同じスケーリングである．

さらに，図4に示すような様々なサンプルサイズでの数値実験でも同様のことが見られ，これらの理論的直観を確認することができる．

\(X_j^n\)の分散が発散しても，それに対応する\(\mu_{n+1}\)と\(\sigma_{n+1}^2\)の推定値がどのようなものなのか，あるいはそれらがオリジナルの\(\mu\)と\(\sigma\)からどの程度離れているのかについての情報は得られない．

特に，ステップn + 1において，真の分布と近似された分布の間の距離がどの程度かを考えたいと思うかもしれない．

これを測定するために，2つの法線間のWasserstein-2距離を考えることができる．

$$ R_{W_2}^{n+1} := W_2^2 (\mathcal{N}(\mu, \sigma^2), \mathcal{N}(\mu_{n+1}, \sigma_{n+1}^2)) = || \mu_{n+1} - \mu ||^2 + || \sigma_{n+1} - \sigma ||^2 $$

これで，有限サンプリングによって発生するリスク，つまり距離の期待値がいくらになるかを計算できる（\(1/M_i\)で展開）．

\begin{eqnarray}
\mathbb{E}_{\mu_{n+1}, \sigma_{n+1}^2} \left[ R_{W_2}^{n+1} \right] &=& \sigma^2 \left( \frac{1}{M_0} + \frac{1}{M_1} + ... + \frac{3}{2M_n} \right) + \mathcal{O}(2) \tag{3} \\
Var_{\mu_{n+1}, \sigma_{n+1}^2} \left[ R_{W_2}^{n+1} \right] &=& \sigma^4 \left( \frac{1}{M_0^2} + \frac{1}{M_1^2} + ... + \frac{3}{M_n^2} + \sum_{i \neq j} \frac{3}{M_i M_j} \right) + \mathcal{O}(3)
\end{eqnarray}

この結果から，モデル崩壊のこの定式化で何が起こるかを正確に解釈することができる．

正確には，近似分布の再サンプリングによる誤差のために，各生成はモデルパラメータのランダムウォークの新しいステップに対応することになる．

このモデルで発生するリスクは，各生成で一定のサンプルサイズに対して発散してしまう．

最終分布の近似が正確で，距離が有限であるためには，サンプリング率\(M_i\)は超線形に増加する必要がある．

つまり，時間をかけて，おそらく2次関数的に，より多くのサンプルを収集する必要がある．

しかし，その場合でもnステップ後の期待距離は0でないままであり，実際に0になる唯一のケースは，各ステップでのサンプリングが無限の場合である．

全体として，これはオリジナルの分布から平均してどの程度離れているかを示しているだけだが，ある生成で推定された分散が十分に小さくなった場合，つまり効果的にデルタ関数になった場合にのみ，プロセスは「終了」することができる．

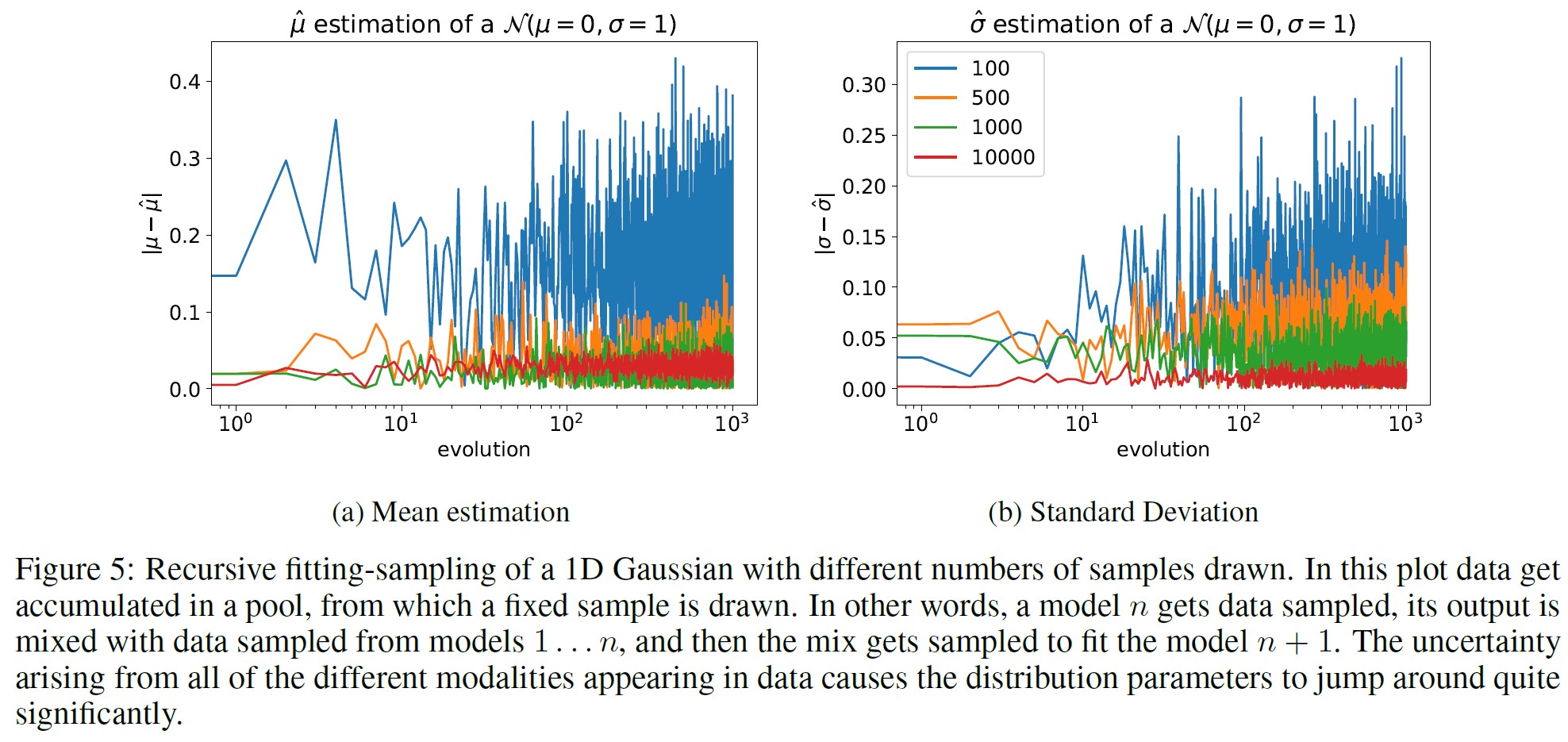
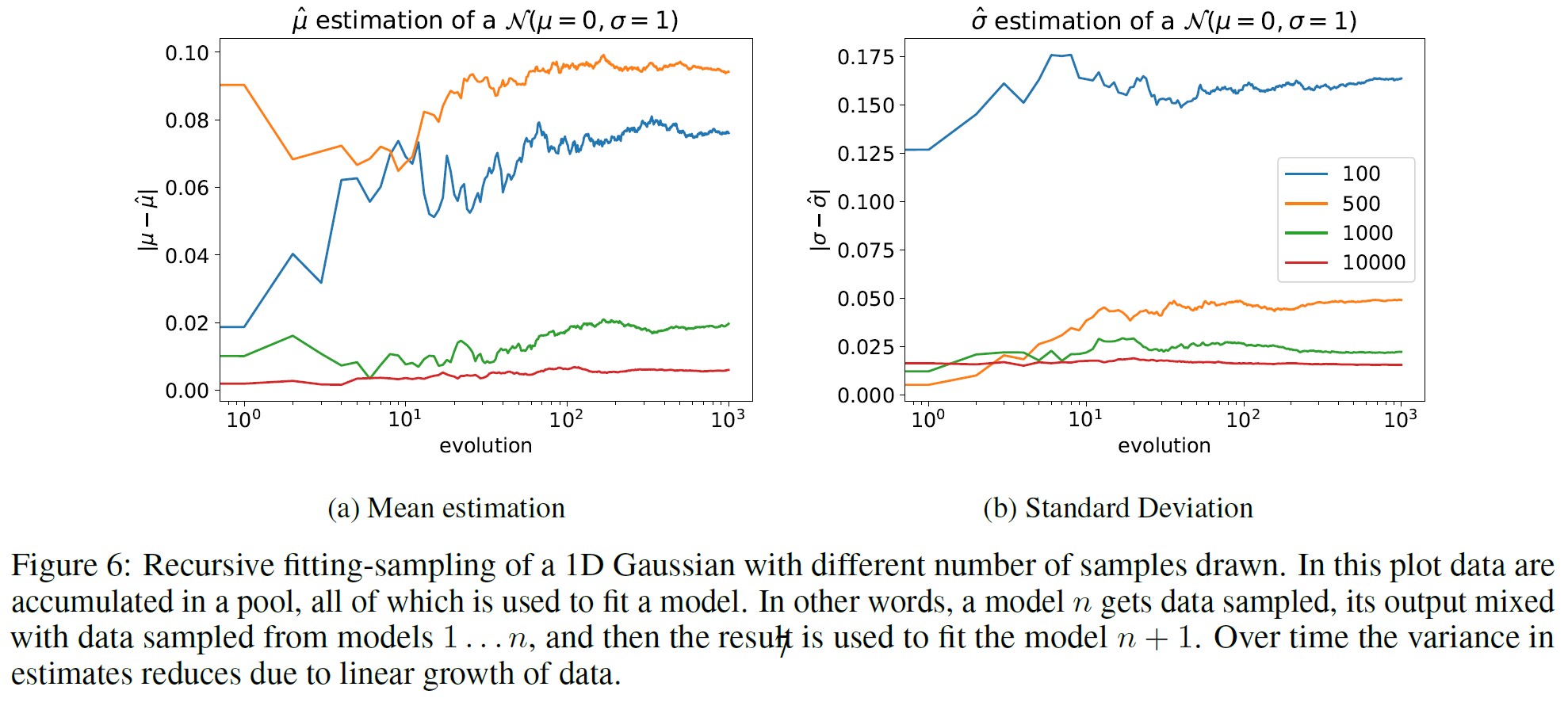
図5と図6は，\(\alpha_i\)，\(\beta_i\)，\(\gamma_i\)のパラメータを異なるサンプルサイズに設定した場合の，このプロセスの異なる実行であり，モデル崩壊を克服するのに十分かどうかを数値的に調べたものである．

しかし，そのような場合であっても，変化は減衰するものの，避けられない．

4.3節：Noisy approximation model（ノイズ近似モデル）

この簡単な例から，n生成分布とオリジナルの分布との距離の下界を構築し，超線形サンプリングなしでも同様にnが大きい極限で発散することを示すことができる．

Wasserstein-2距離の素晴らしい性質は，ガウス分布がWasserstein距離の普遍的な下界を提供することである[Gelbrich, 1990]．

特に，\(\mu_\kappa\)と\(\mu_\nu\)の平均，\(\sum_\kappa\)と\(\sum_\nu\)の共分散行列を持つユークリッドN次元空間上の\(\kappa\)と\(\nu\)の確率測度に対して，次の式が得られる．

$$ W_2^2 (\kappa, \nu) \geq || \mu_\kappa - \mu_\nu ||^2 + Tr \left( \Sigma_\kappa + \Sigma_\nu - 2 \left( \Sigma_\kappa^{1/2} \Sigma_\nu \Sigma_\kappa^{1/2} \right)^{1/2} \right) \geq || \mu_\kappa - \mu_\nu ||^2 $$

これにより，距離を正確に定量化する代わりに，その距離の下界を形成することができる．

唯一の制限は，関数近似モデルを指定しなければならないということである．

\(W_2\)境界を達成するためには，平均が生成間でどのように変化するかを特定する必要がある．

標本平均しか入手できないシナリオでは，次の生成分布の平均を式1のように近似する．

しかし，より多くの情報が入ってきたり，モデルがその情報をうまく使い始めたりすると，標本平均から乖離してしまうかもしれない．

この場合でも，モデルの性能が良いこと，つまり平均推定値が同じであることが必要である．

また，分散計算に対するモデルの期待される振る舞いを指定しなければならないが，これも平均化されるように選択される．

従って，我々は次のような生成間の進化を採用する．

$$ \mu_{i+1} = \frac{1}{M_i} \sum_j X_j^i + \varepsilon_{i+1} = \frac{\sum_i^{1/2}}{\sqrt{M_i}} T^{i+1} + \mu_i + \varepsilon_{i+1}; \ \ \ \mathbb{E}_{X_j^i} ( \Sigma_{i+1} ) = \Sigma_i $$

ここで\(T^{i+1}\)は上式を満たすように定義される，すなわち\(T^{i+1} = \frac{\sum_i^{-1/2}}{\sqrt{M_i}} \Sigma_j (X_j^i - \mu_i)\)．

この正規化により，Tは平均0，共分散\(I_N\)となり，中心極限定理（CLT：Central Limit Theorem）により，\(T^{i+1}| \mu_i, \Sigma_i \xrightarrow{\mathcal{D}} \mathcal{N}(0, I_N)\)となるが，下界はこれに依存しない．

式3と同様のリスクの下界を得るためには，\(\varepsilon_{i+1}\)の形式についていくつかの仮定をする必要がある．

仮定：

1. 平均すると，反復前と同じになる．
   $$ \mathbb{E}[\varepsilon_{i+1}|\mu_i, \Sigma_i] = 0 $$
2. すべての\(X_j^i\)が与えられたとき，\(\varepsilon\)は一定でなければならない．すなわち，データだけの関数である．
   $$ \varepsilon_{i+1} = \varepsilon_{i+1} (X_j^i) $$
   特に，\(\mu_i\)と\(\sum_i\)にはデータを通じてのみ依存する．
3. 余分なノイズは，確率変数の意味で標本平均に直交する．これは事実上，ノイズがいかなるファーストモーメント情報も含んでいないと仮定していることになる．すなわち下式が成立する．
   $$ Cov(\varepsilon_{i+1}, T^{i+1} | \mu_i, \Sigma_i) = 0 $$
   これは，これまでの仮定と比べると，かなり強い仮定であるように思われるかもしれないが，この性質は，\(M_i\)が大きい極限で\(T^{i+1}\)にCLTを課し（ここでは，\(M_i\)は大きいと仮定するだけで，無限大ではないことに注意），\(\varepsilon\)が厳密にはファーストモーメントより大きいモーメントの関数であると仮定したときに成り立つことを示すことができる．さらに，このタイプの性質は，実際に何らかの情報を提供するために必要である．それ以前は，\(\varepsilon\)項と標本平均項に分離する必要はなく，すべてが\(\varepsilon\)に吸収されるからである．

付録A.2では，さらに仮定3の代替案を提示し，ノイズの大きさを制限することで，\(1/M_i\)の展開としてのみ，以下の境界を回復することができる．

すべての仮定が整ったので，次のような境界が得られた．

\begin{eqnarray}
\mathbb{E} \left[R_{W^2}^{i+1} \right] &\geq& \mathbb{E} (|| \mu_{i+1} - \mu ||^2) \\
&=& \mathbb{E} (|| \mu_i - \mu ||^2) + \mathbb{E}(||\varepsilon_{i+1}||^2) + \frac{1}{M_i} \mathbb{E}((T^{i+1})^\top \Sigma_i (T^{i+1})) \\
&+& \frac{2}{\sqrt{M_i}} \mathbb{E} \left( (\varepsilon_{i+1})^\top \Sigma_i^{1/2} T^{i+1} + (\mu_i - \mu)^\top \Sigma_i^{1/2} T^{i+1} \right) \\
&=& \mathbb{E}(||\mu_i - \mu||^2) + \frac{Tr \Sigma}{M_i} + \mathbb{E}(||\varepsilon_{i+1}||^2) + \frac{2}{\sqrt{M_i}} \mathbb{E} \left( (\varepsilon_{i+1})^\top \Sigma_i^{1/2} T^{i+1} \right)
\end{eqnarray}

今，評価すべき唯一の量は，仮定3によると下式である．

$$ \frac{2}{\sqrt{M_i}} \mathbb{E} \left( (\varepsilon_{i+1})^\top \Sigma_i^{1/2} T^{i+1} \right) = \frac{2}{\sqrt{M_i}} \int d \Sigma_i p(\Sigma_i) Tr \left[ \Sigma_i^{1/2} Cov(\varepsilon_{i+1}, T^{i+1} | \Sigma_i ) \right] = 0 $$

したがって，全体的な境界はガウスの場合と似ているが，ノイズの分散項が追加されている．

$$ \mathbb{E}_{\mu_{n+1}, \sigma_{n+1}^2} \left[ R_{W_2}^{n+1} \right] \geq Tr \Sigma \left( \frac{1}{M_0} + \frac{1}{M_1} + ... + \frac{1}{M_n} \right) + \sum_{i=1}^{n+1} \mathbb{E}(||\varepsilon_i||^2) $$

その結果，ステップi + 1での平均が標本平均と「余分な」平均に直交して分離できるような，より一般的な近似モデルの場合でも，モデル崩壊の下界を最小化するために同じ超線形スケーリングが必要であることが示された．

全体として，本章のメッセージは以下のように要約できる．

5章：Evaluation（評価）

5.1節：Training from scratch with GMMs and VAEs（GMMとVAEによるゼロからのトレーニング）

ガウス混合モデル：

この節では，ガウス混合モデル（Gaussian Mixture Models: GMMs）[Reynolds et al., 2009]の性能を評価する．

ここでの基礎タスクは，与えられたGMMが2つの人工的に生成されたガウシアンを分離しようとすることである．

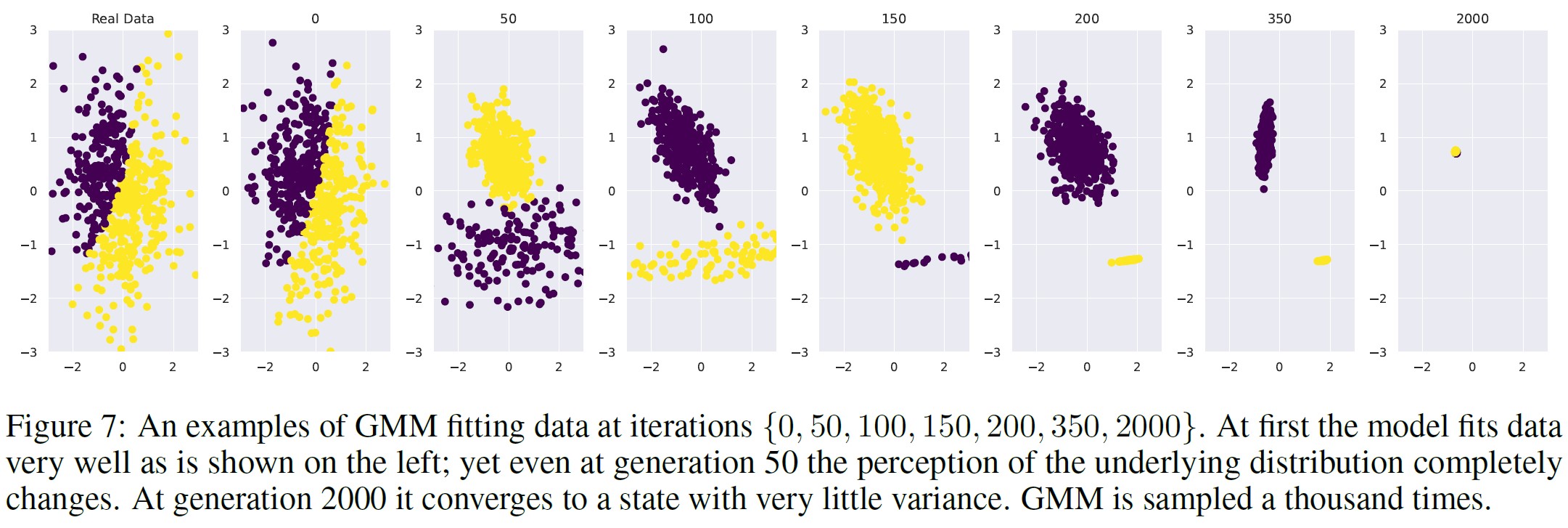
図7は，GMMフィッティングプロセスの時間経過を示す．

一番左のプロットは，オリジナルの2つのガウシアンとグランドトゥルースラベルを示す．

次のプロットは，誤差が最小となる\(\alpha_i = \gamma_i = 0\)，つまり生成を超えたデータを使用しないオリジナルデータにフィットしたGMMを示している．

しかし，再サンプリングを50回繰り返すうちに，根本的な分布が誤って認識されるポイントに到達する．

性能は時間とともに悪化し，反復2000までには，ほとんど分散のない分布の点推定に到達する．オリジナルのGMMとその子孫の間のL2距離を図13にプロットする．

変分オートエンコーダ：

この節では，変分オートエンコーダ（VAE）について述べる．

先程と同様に，オートエンコーダをオリジナルのデータソースで訓練し，それを後でサンプリングする．

ここでは，ガウス分布から潜在変数を生成し，それをデコーダが次の生成のためのデータを生成するために使用する．

左の図9は，[Kingma and Welling, 2022]が説明した設定を使って生成したデータの例である．

※訳注：図8は後述します．

この処理を何度も行ううちに，データから学習したオリジナルのクラスとはほとんど似ていない表現にたどり着く．

右側は20番目の生成から作られた画像で，すべての異なる数字が混在しているように見える．

興味深いことに，オリジナルのエンコーダは，その子孫から生成されたデータを，ますます信頼性を増して知覚している．

エンコーダはこのようなデータを平均にどんどん近づけていく．

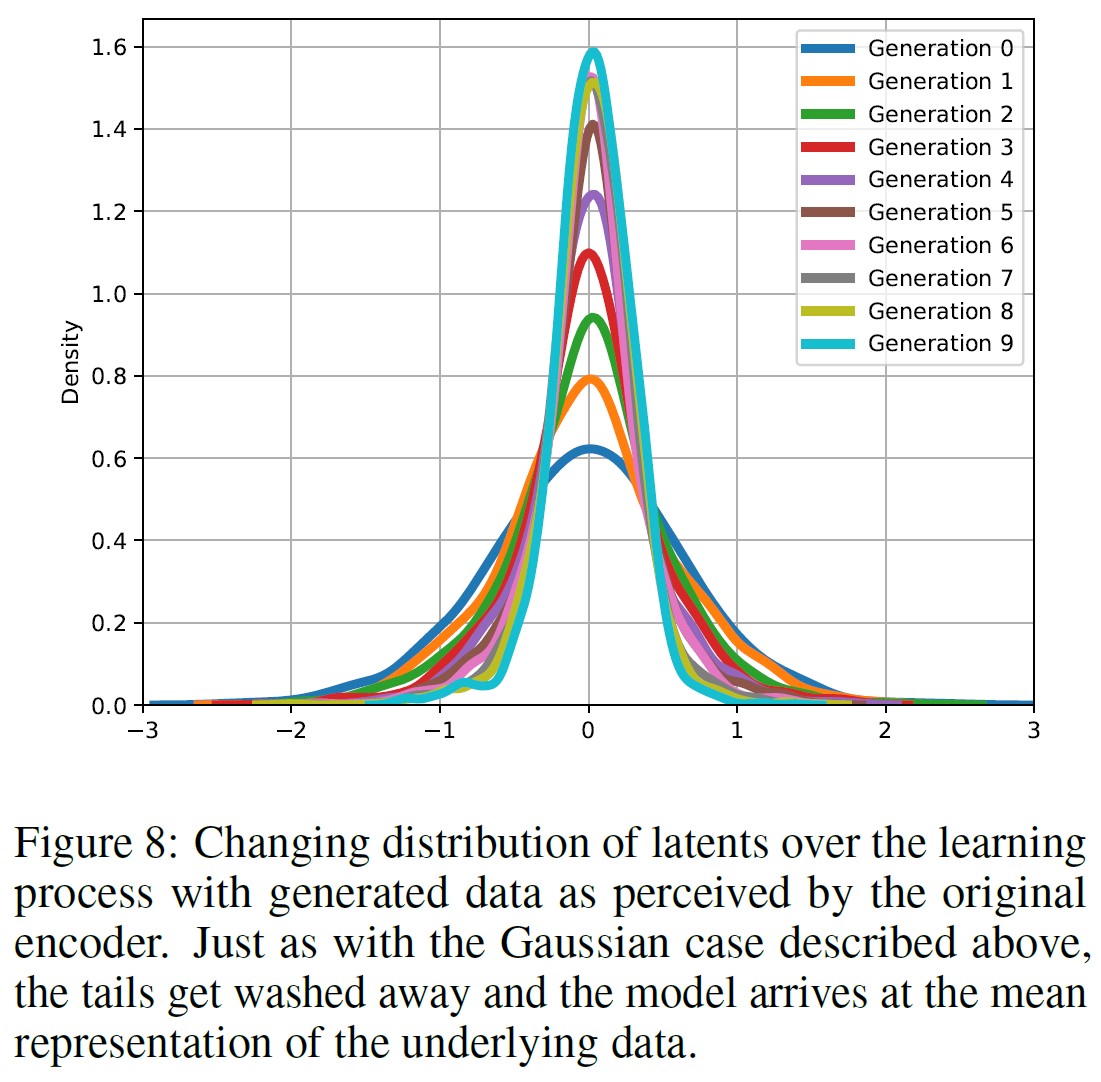
図8は，その子孫によって生成されたデータを提示したときの，オリジナルのモデルにおける潜在的表現の密度を示している．

1次元のガウシアンと同様に，時間の経過とともにテールは消え，密度はすべて平均に向かってシフトする．

5.2節：Language Models（言語モデル）

ここまでで，モデル崩壊がMLモデルの異なるファミリーに普遍的であることは明らかである．

しかし，GMMやVAEなどの小さなモデルは通常ゼロから訓練されるとすると，LLMは異なる．

ゼロから再訓練するのは非常にコストがかかるため，通常，BERT[Devlin et al., 2018]，RoBERTa[Liu et al., 2019]，GPT2[Brown et al., 2020]など，大規模なテキストコーパスで訓練された事前訓練済みモデルで初期化される．

その後，様々な下流タスクに合わせてファインチューニングされる[Bommasani et al., 2022]．

この節では，言語モデルが他のモデルによって生成されたデータで順次ファインチューニングされた場合に何が起こるかを探る．

※5.1節で説明した実験を言語モデルで簡単に再現し，モデル崩壊を実証することができる．中程度の大きさのモデルを1つ訓練すると，アメリカ人の一生分の2倍の\(CO_2\)が発生する[Strubell et al., 2019]ことを考えると，我々はそのような実験を行わず，代わりに概念実証（PoC：Proof-of-Concept）のためのより現実的な設定に焦点を当てることを選択した．論文に記載されている言語実験だけでも，実行に数週間を要したことに注意されたい．

ここでは，言語モデルの訓練で最も一般的な設定である，訓練サイクルがそれぞれ最近のデータで事前訓練されたモデルから始まるファインチューニング設定を評価する．

ここでのデータは，別のファインチューニングされた事前訓練されたモデルから得られる．

訓練は，オリジナルの訓練済みモデルに近いモデルを生成するように制限され，モデルによって生成されるデータポイントは一般的に非常に小さな勾配を生成する．

ここで期待されるのは，ファインチューニング後にモデルが適度にしか変化しないかもしれない．

我々は，Huggingface[Zhang et al., 2022]を通じてMetaが提供するOPT-125m因果言語モデルをファインチューニングする．

wikitext2データセットでモデルをファインチューニングする．

訓練済みモデルからのデータ生成には，5-way beam-searchを使用する．

訓練シーケンスは64トークンの長さになるようにブロックする．

次に，訓練セットの各トークンシーケンスに対して，次の64トークンを予測するようモデルに求める．

オリジナルの訓練データセットをすべて調べ，同じサイズの人工データセットを作成する．

オリジナルのデータセットをすべて調べ，すべてのブロックを予測するので，モデルの誤差が0.0であれば，オリジナルのwikitext2データセットを生成することになる．

各生成の訓練は，オリジナルの訓練データから生成することから始める．

各実験は5回実行され，結果は5回の別々の実行として示される．

実際のwikitext2データでファインチューニングされたオリジナルのモデルは，zero-shotのベースライン115から34の平均パープレキシティを得る（タスクの学習に成功する）．

最後に，可能な限り現実的にするために，オリジナルのwikitext2検証セットを使って評価された，オリジナルのタスクで最もパフォーマンスの良いモデルを，後続生成の基本モデルとして使用する．

実際に観測されたモデル崩壊は，さらに顕著になる可能性がある．

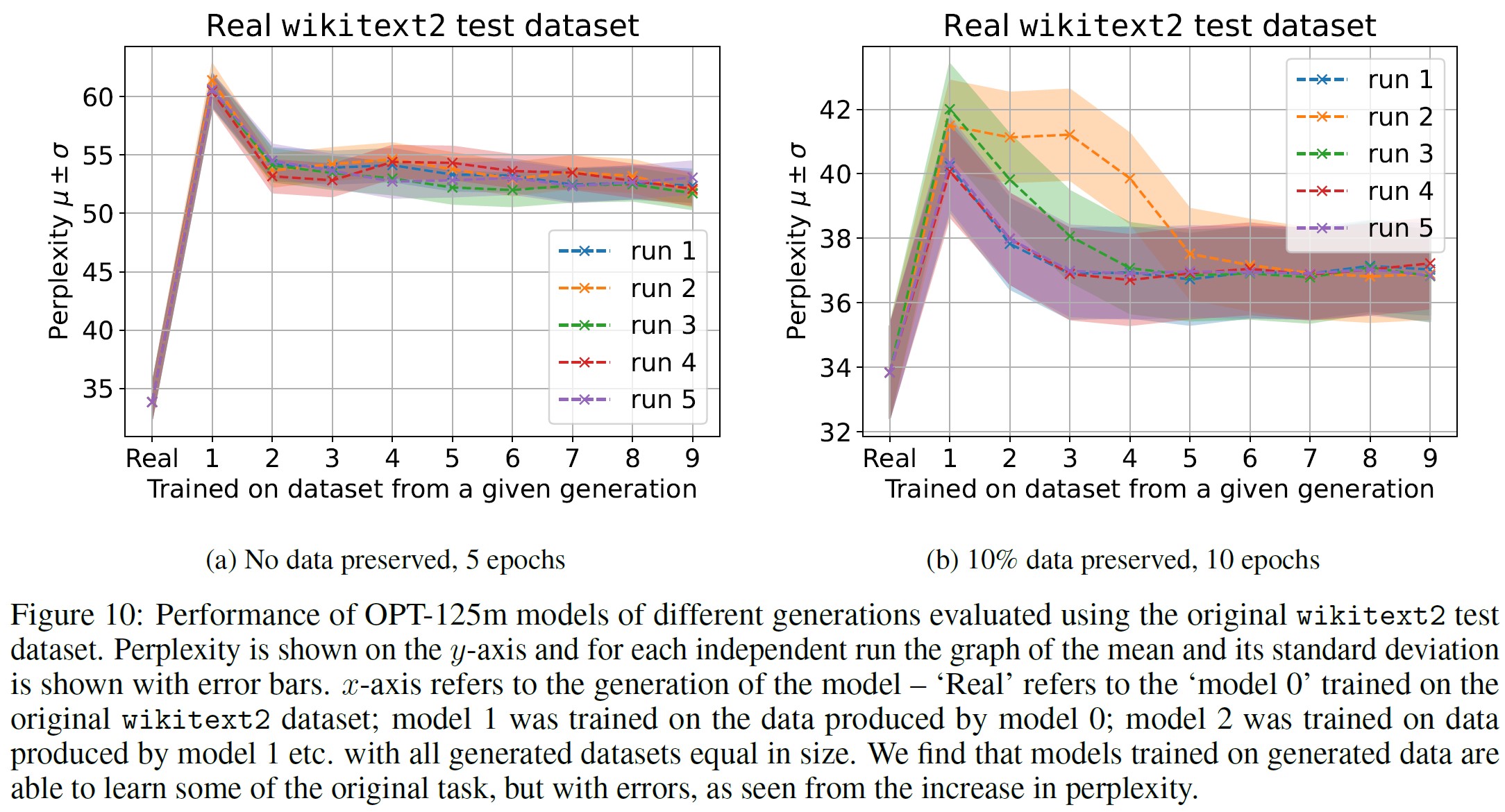
ここでは2つの異なるセッティングを考える．

• 5エポック，オリジナルの訓練データなし：ここでは，オリジナルデータセットとオリジナルデータなしでモデルを5エポック訓練させる．全体的なオリジナルのタスクの性能は図10（a）に示されている．生成されたデータで訓練することで，20から28パープレキシティポイントの性能を失いながらも，基礎タスクに適応できることがわかる．
• 10エポック，オリジナルの訓練データの10%を保存：ここでは，モデルはオリジナルのデータセットで10エポック訓練され，新しい生成の訓練ごとに，オリジナルのデータポイントのランダムな10%がサンプリングされる．図10（b）に全体的なオリジナルタスクのパフォーマンスを示す．オリジナルのデータを保存することで，より良いモデルのファインチューニングが可能になり，性能の劣化はわずかであることがわかる．

どちらの訓練方式も，我々のモデルのパフォーマンスを低下させる．

しかし，生成されたデータを使った学習は可能であり，モデルは基礎タスクの（一部の）学習に成功することがわかった．

次に，我々のモデルの各生成における，起こりうる出来事の基本的な認識について考えてみる．

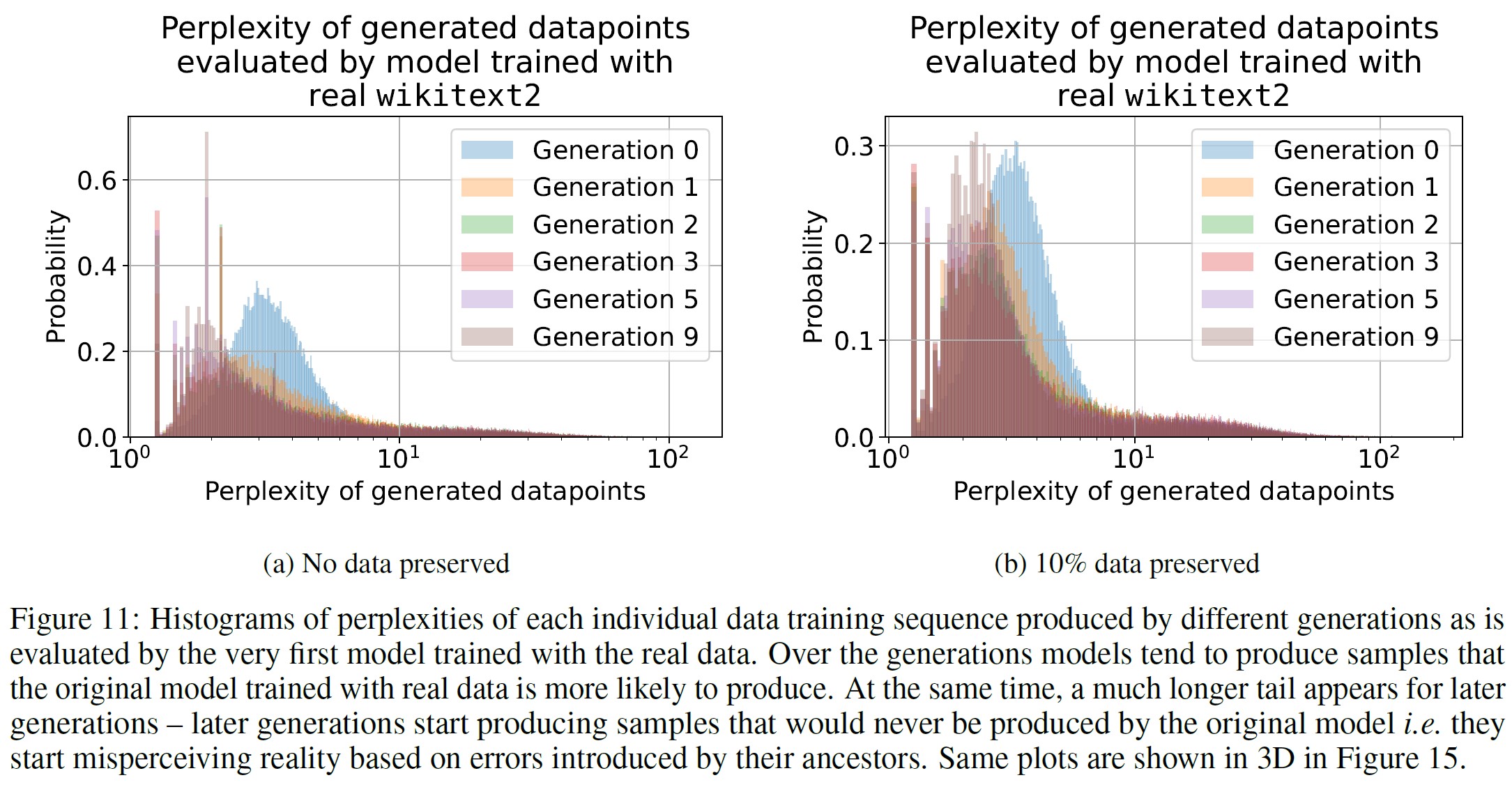
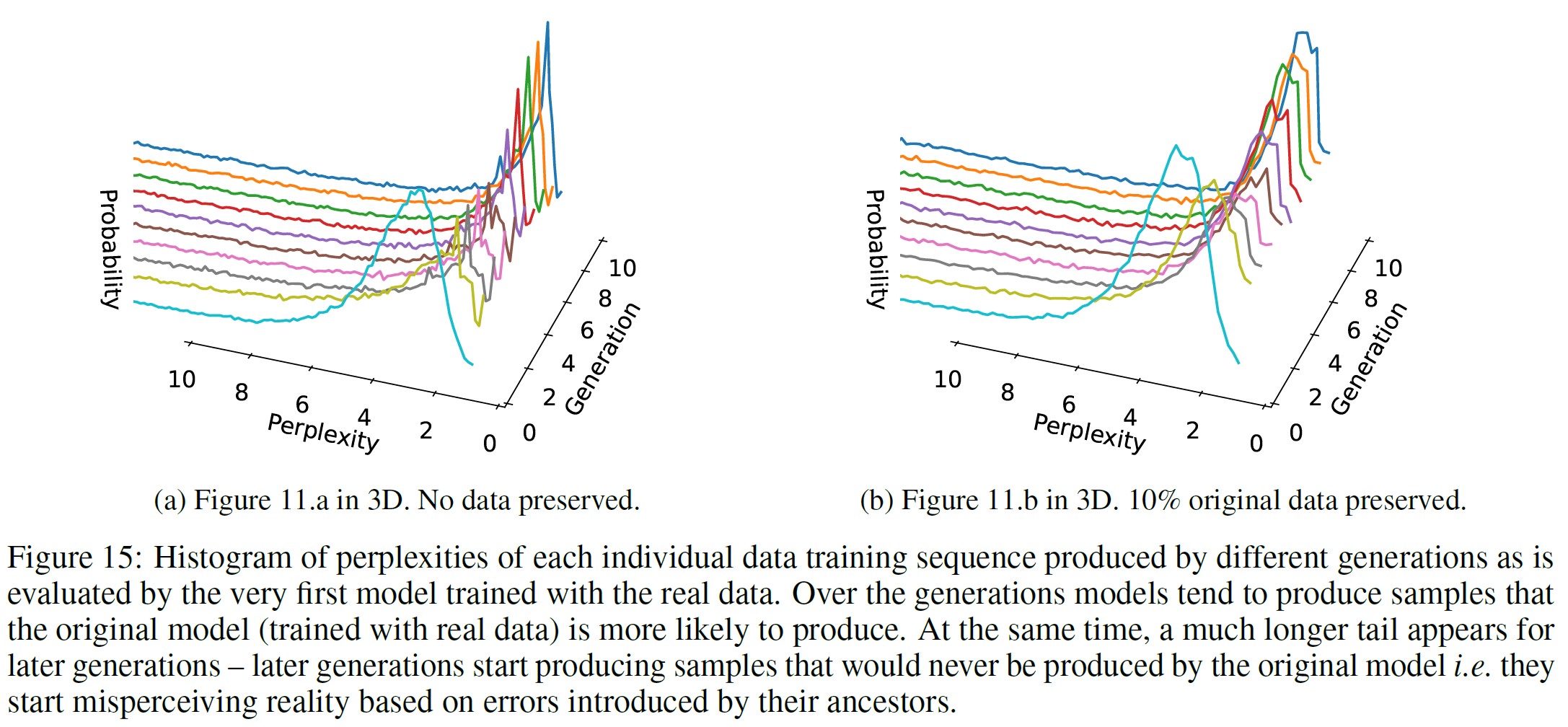
図11は，実際のwikitext2訓練データを用いて開発された最初のモデルによって評価された，異なる生成モデルによって作られた個々のデータポイントのパープレキシティのヒストグラムである．

生成が進むにつれて，モデルはオリジナルのモデルがより高い尤度で生成するであろうシーケンスをより多く生成する傾向がある．

観察された効果は，5.1節でVAEとGMMについて説明したものと似ており，生成が進むにつれて，モデルはオリジナルのモデルにより高い確率で生成されるサンプルを生成し始める．

同時に，我々は，生成されたデータがより長いテールを持つことを発見し，データの一部はオリジナルのモデルでは生成されないことを示唆する．

これらは，生成データを使った学習のために蓄積されたエラーである．

我々の実験では，言語モデルによって生成されたデータには，繰り返しフレーズが大量に含まれてしまうことがわかった．

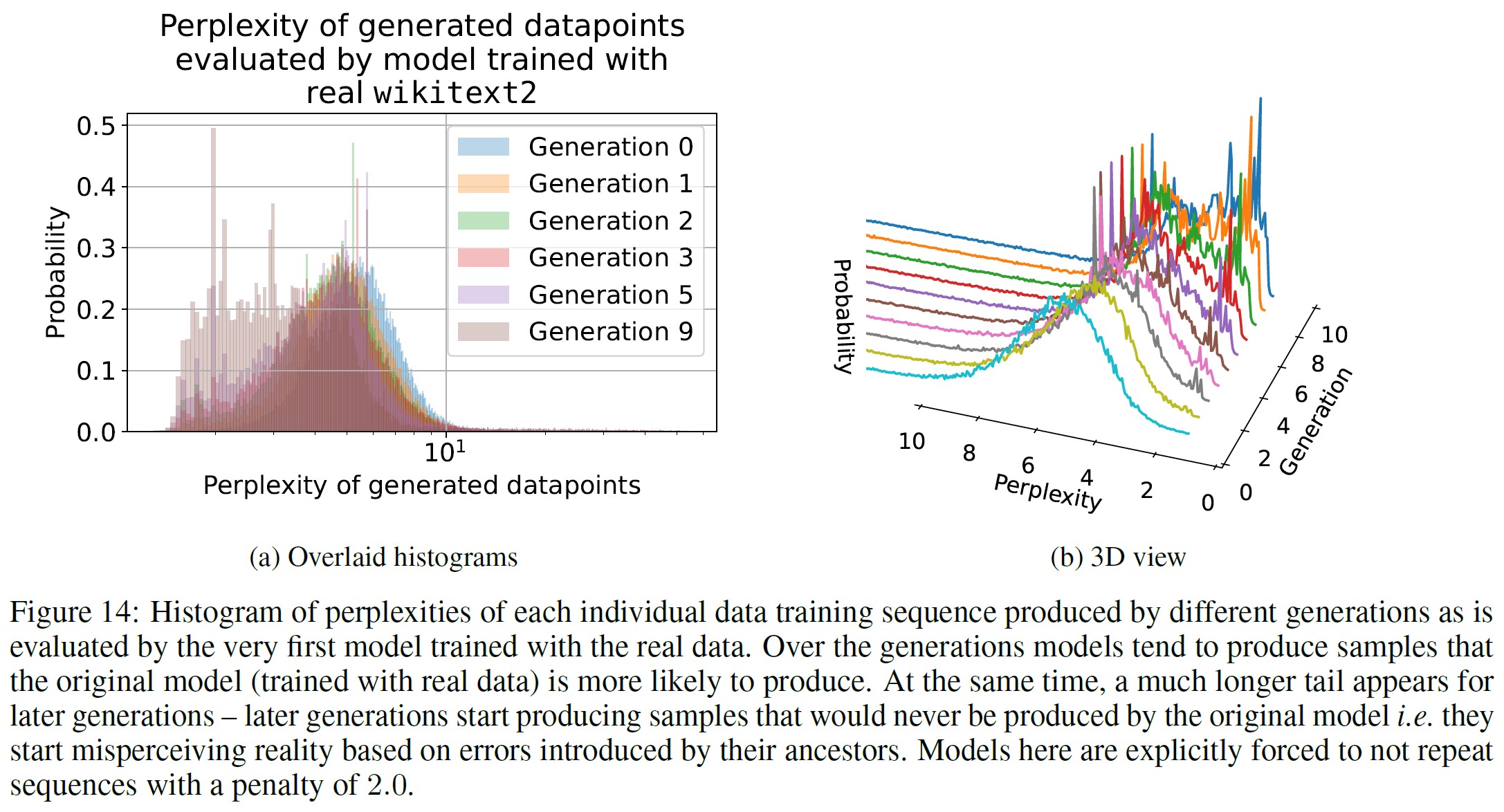
繰り返し問題は，ほぼ全てのテキスト生成モデルで観察されており[Keskar et al., 2019, Shumailov et al., 2021]，モデル崩壊の原因としてこれを除外するために，さらに，モデルが明示的に繰り返しペナルティー2.0の非繰り返しシーケンスを生成するよう促された場合の数値実験を提供する．

この結果，モデルは繰り返しの使用を避けるために，より低いスコアの連続を生成するようになり，結果的にモデルの性能がさらに低下することがわかった．

図14は，モデルの複雑さが生成間でより確率の高いトークン列にシフトしていることを示している．

特にLLM実験では，これを強制することで，オリジナルのモデルに比べてパープレキシティが2倍になる．

モデルはモデル崩壊の影響を受けやすい．

このプロセスは，言語モデルのファインチューニングがモデル崩壊の影響を抑制せず，ファインチューニング中のモデルも脆弱であることを示している．

生成を重ねるにつれて，モデルはオリジナルのデータからより確率の高いシーケンスを生成する傾向があり，独自のあり得ないシーケンス，つまりエラーを導入し始めることがわかる．

6章：Discussion and Conclusion（ディスカッションと結論）

ここで，モデル崩壊がLLMの基本的な学習ダイナミクスに与える影響について議論する．

言語モデルに対する長期的なポイズニング攻撃は新しいものではない．

例えば，クリックファーム，コンテンツファーム，トロールファームといった，ソーシャルネットワークや検索アルゴリズムを誤誘導することを仕事とする，人間の「言語モデル」のようなものが作られた．

このようなポイズニング攻撃が検索結果に与えた悪影響は，検索アルゴリズムの変更につながった．

例えば，グーグルはファーム化された記事を格下げし，教育ドメインなどの信頼できるソースによって作成されたコンテンツをより重視するようになり，DuckDuckGoはそれらを完全に削除した．

LLMの登場によって異なるのは，ひとたび自動化されると，このようなポイズニングが起こりうる規模が大きくなることである．

LLMが確率の低い事象をモデル化する能力を維持することは，その予測の公平性を保つために不可欠である．

このような事象は，しばしば社会から疎外されたグループに関連する．

確率の低い事象は，複雑なシステムを理解するためにも不可欠である[Taleb, 2007]．

我々の評価は，LLMのようなモデルの訓練に関して，「先行者利益」を示唆している．

我々の研究では，別の生成モデルからのサンプルで訓練することで，分布のシフトを誘発し，それが時間の経過とともにモデル崩壊を引き起こすことを実証している．

その結果，モデルは基礎学習タスクを誤認識するようになる．

学習が長期間にわたって持続するようにするには，オリジナルのデータソースへのアクセスが維持され，LLMによって生成されたのではない追加データが長期間にわたって利用可能であることを確認する必要がある．

LLMによって生成されたデータを他のデータと区別する必要性から，インターネットからクロールされたコンテンツの出所に関する疑問が生じる．

LLMによって生成されたコンテンツを，どのようにして大規模に追跡できるかは不明である．

1つの選択肢は，LLMの作成と展開に関わるさまざまな関係者が，出所に関する疑問を解決するために必要な情報を共有できるよう，コミュニティ全体で調整することである．

そうでなければ，この技術が大量に採用される前にインターネットからクロールされたデータにアクセスしたり，人間が大規模に生成したデータに直接アクセスしたりすることなく，新しいバージョンのLLMを訓練することはますます難しくなるかもしれない．

References（参考文献）

1. [Aljundi et al., 2018] Rahaf Aljundi, Francesca Babiloni, Mohamed Elhoseiny, Marcus Rohrbach, and Tinne Tuytelaars. Memory aware synapses: Learning what (not) to forget. In Proceedings of the European conference on computer vision (ECCV), pages 139–154, 2018.
2. [Aljundi et al., 2019] Rahaf Aljundi, Klaas Kelchtermans, and Tinne Tuytelaars. Task-free continual learning. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, pages 11254–11263, 2019.
3. [Biggio et al., 2012] Battista Biggio, Blaine Nelson, and Pavel Laskov. Poisoning attacks against support vector machines. arXiv preprint arXiv:1206.6389, 2012.
4. [Bommasani et al., 2022] Rishi Bommasani, Drew A. Hudson, Ehsan Adeli, Russ Altman, Simran Arora, Sydney von Arx, Michael S. Bernstein, Jeannette Bohg, Antoine Bosselut, Emma Brunskill, Erik Brynjolfsson, Shyamal Buch, Dallas Card, Rodrigo Castellon, Niladri Chatterji, Annie Chen, Kathleen Creel, Jared Quincy Davis, Dora Demszky, Chris Donahue, Moussa Doumbouya, Esin Durmus, Stefano Ermon, John Etchemendy, Kawin Ethayarajh, Li Fei-Fei, Chelsea Finn, Trevor Gale, Lauren Gillespie, Karan Goel, Noah Goodman, Shelby Grossman, Neel Guha, Tatsunori Hashimoto, Peter Henderson, John Hewitt, Daniel E. Ho, Jenny Hong, Kyle Hsu, Jing Huang, Thomas Icard, Saahil Jain, Dan Jurafsky, Pratyusha Kalluri, Siddharth Karamcheti, Geoff Keeling, Fereshte Khani, Omar Khattab, Pang Wei Koh, Mark Krass, Ranjay Krishna, Rohith Kuditipudi, Ananya Kumar, Faisal Ladhak, Mina Lee, Tony Lee, Jure Leskovec, Isabelle Levent, Xiang Lisa Li, Xuechen Li, Tengyu Ma, Ali Malik, Christopher D. Manning, Suvir Mirchandani, Eric Mitchell, Zanele Munyikwa, Suraj Nair, Avanika Narayan, Deepak Narayanan, Ben Newman, Allen Nie, Juan Carlos Niebles, Hamed Nilforoshan, Julian Nyarko, Giray Ogut, Laurel Orr, Isabel Papadimitriou, Joon Sung Park, Chris Piech, Eva Portelance, Christopher Potts, Aditi Raghunathan, Rob Reich, Hongyu Ren, Frieda Rong, Yusuf Roohani, Camilo Ruiz, Jack Ryan, Christopher Ré, Dorsa Sadigh, Shiori Sagawa, Keshav Santhanam, Andy Shih, Krishnan Srinivasan, Alex Tamkin, Rohan Taori, Armin W. Thomas, Florian Tramèr, Rose E. Wang, William Wang, Bohan Wu, Jiajun Wu, Yuhuai Wu, Sang Michael Xie, Michihiro Yasunaga, Jiaxuan You, Matei Zaharia, Michael Zhang, Tianyi Zhang, Xikun Zhang, Yuhui Zhang, Lucia Zheng, Kaitlyn Zhou, and Percy Liang. On the opportunities and risks of foundation models, 2022.
5. [Brown et al., 2020] Tom Brown, Benjamin Mann, Nick Ryder, Melanie Subbiah, Jared D Kaplan, Prafulla Dhariwal, Arvind Neelakantan, Pranav Shyam, Girish Sastry, Amanda Askell, et al. Language models are few-shot learners. Advances in neural information processing systems, 33:1877–1901, 2020.
6. [Carlini and Terzis, 2021] Nicholas Carlini and Andreas Terzis. Poisoning and backdooring contrastive learning. arXiv preprint arXiv:2106.09667, 2021.
7. [Carlini et al., 2023] Nicholas Carlini, Matthew Jagielski, Christopher A Choquette-Choo, Daniel Paleka, Will Pearce, Hyrum Anderson, Andreas Terzis, Kurt Thomas, and Florian Tramèr. Poisoning web-scale training datasets is practical. arXiv preprint arXiv:2302.10149, 2023.
8. [Cochran, 1934] W. G. Cochran. The distribution of quadratic forms in a normal system, with applications to the analysis of covariance. Mathematical Proceedings of the Cambridge Philosophical Society, 30(2):178–191, 1934. doi: 10.1017/S0305004100016595.
9. [Devlin et al., 2018] Jacob Devlin, Ming-Wei Chang, Kenton Lee, and Kristina Toutanova. Bert: Pre-training of deep bidirectional transformers for language understanding. arXiv preprint arXiv:1810.04805, 2018.
10. [Fischer et al., 2023] Adrian Fischer, Robert E. Gaunt, and Andrey Sarantsev. The variance-gamma distribution: A review, 2023.
11. [Gelbrich, 1990] Matthias Gelbrich. On a formula for the l2 wasserstein metric between measures on euclidean and hilbert spaces. Mathematische Nachrichten, 147(1):185–203, 1990.
12. [Griffith et al., 2013] Shane Griffith, Kaushik Subramanian, Jonathan Scholz, Charles L Isbell, and Andrea L Thomaz. Policy shaping: Integrating human feedback with reinforcement learning. In C.J. Burges, L. Bottou, M. Welling, Z. Ghahramani, and K.Q. Weinberger, editors, Advances in Neural Information Processing Systems, volume 26. Curran Associates, Inc., 2013. URL https://proceedings.neurips.cc/paper_files/paper/2013/file/e034fb6b66aacc1d48f445ddfb08da98-Paper.pdf.
13. [Gu et al., 2017] Tianyu Gu, Brendan Dolan-Gavitt, and Siddharth Garg. Badnets: Identifying vulnerabilities in the machine learning model supply chain. arXiv preprint arXiv:1708.06733, 2017.
14. [Keskar et al., 2019] Nitish Shirish Keskar, Bryan McCann, Lav R. Varshney, Caiming Xiong, and Richard Socher. Ctrl: A conditional transformer language model for controllable generation, 2019.
15. [Kingma and Welling, 2022] Diederik P Kingma and Max Welling. Auto-encoding variational bayes, 2022.
16. [Kirkpatrick et al., 2017] James Kirkpatrick, Razvan Pascanu, Neil Rabinowitz, Joel Veness, Guillaume Desjardins, Andrei A Rusu, Kieran Milan, John Quan, Tiago Ramalho, Agnieszka Grabska-Barwinska, et al. Overcoming catastrophic forgetting in neural networks. Proceedings of the national academy of sciences, 114(13):3521–3526, 2017.
17. [Li and Hoiem, 2017] Zhizhong Li and Derek Hoiem. Learning without forgetting. IEEE transactions on pattern analysis and machine intelligence, 40(12):2935–2947, 2017.
18. [Liu et al., 2019] Yinhan Liu, Myle Ott, Naman Goyal, Jingfei Du, Mandar Joshi, Danqi Chen, Omer Levy, Mike Lewis, Luke Zettlemoyer, and Veselin Stoyanov. Roberta: A robustly optimized bert pretraining approach. arXiv preprint arXiv:1907.11692, 2019.
19. [Nguyen et al., 2015] Anh Nguyen, Jason Yosinski, and Jeff Clune. Deep neural networks are easily fooled: High confidence predictions for unrecognizable images, 2015.
20. [OpenAI, 2023] OpenAI. Gpt-4 technical report, 2023.
21. [Radford et al., 2021] Alec Radford, Jong Wook Kim, Chris Hallacy, Aditya Ramesh, Gabriel Goh, Sandhini Agarwal, Girish Sastry, Amanda Askell, Pamela Mishkin, Jack Clark, et al. Learning transferable visual models from natural language supervision. In International conference on machine learning, pages 8748–8763. PMLR, 2021.
22. [Reynolds et al., 2009] Douglas A Reynolds et al. Gaussian mixture models. Encyclopedia of biometrics, 741(659-663), 2009.
23. [Shumailov et al., 2021] Ilia Shumailov, Yiren Zhao, Daniel Bates, Nicolas Papernot, Robert Mullins, and Ross Anderson. Sponge examples: Energy-latency attacks on neural networks. In 2021 IEEE European Symposium on Security and Privacy (EuroS&P), pages 212–231. IEEE, 2021.
24. [Solaiman et al., 2019] Irene Solaiman, Miles Brundage, Jack Clark, Amanda Askell, Ariel Herbert-Voss, Jeff Wu, Alec Radford, Gretchen Krueger, Jong Wook Kim, Sarah Kreps, Miles McCain, Alex Newhouse, Jason Blazakis, Kris McGuffie, and Jasmine Wang. Release strategies and the social impacts of language models, 2019.
25. [Strubell et al., 2019] Emma Strubell, Ananya Ganesh, and Andrew McCallum. Energy and policy considerations for deep learning in nlp. arXiv preprint arXiv:1906.02243, 2019.
26. [Taleb, 2007] Nassim Nicholas Taleb. Black swans and the domains of statistics. The American Statistician, 61(3):198–200, 2007.
27. [Van de Ven and Tolias, 2019] Gido M Van de Ven and Andreas S Tolias. Three scenarios for continual learning. arXiv preprint arXiv:1904.07734, 2019.
28. [Zhang et al., 2022] Susan Zhang, Stephen Roller, Naman Goyal, Mikel Artetxe, Moya Chen, Shuohui Chen, Christopher Dewan, Mona Diab, Xian Li, Xi Victoria Lin, et al. Opt: Open pre-trained transformer language models. arXiv preprint arXiv:2205.01068, 2022.

付録A：Appendix（付録）

付録A.1：Absorbing Markov Chain（吸収マルコフ連鎖）

この節では，吸収マルコフ連鎖が確率1で吸収状態に収束するという，吸収マルコフ連鎖に関するよく知られた事実を説明する．

\(\mathbf{X}^m\)がマルコフ連鎖を形成していると仮定する．

この連鎖を推論するためには，遷移確率を考える必要がある．

一般に，これらは我々の関数近似スキームに対応する．

マルコフ連鎖の確率的性質から，分散が上下することが予想される．

しかし分散が減少するにつれて，新たにサンプリングされたデータは，その有限性により，より集中し，極限ではすなわちデルタ関数の集合につながる．

この議論は，近似スキームが良好でデルタ関数に収束できることを前提としている．

そうでない場合，近似の誤差が確率の誤差の伝播を妨げる可能性がある．

先述した章で説明したように，「サンプリング」と「フィッティング」を繰り返すプロセスをマルコフ連鎖としてモデル化することができる．

この節では，このようなプロセスがどのようにして定常状態，つまりマルコフ連鎖の吸収状態に収束するかを説明する．

この導出ではAllan Yashinskiに従う．

r個の過渡状態\(t_1,…,t_r\)とs個の吸収状態\(a_1,…,a_s\)の吸収マルコフ連鎖を持つと仮定する．

マルコフ連鎖全体はr + s個の状態を持ち，\(t_1,…,t_r,a_1,…,a_s\)のように並べられる．

遷移行列は次のように定義される．

\begin{eqnarray}
T =
\begin{bmatrix}
Q & 0_{r*s} \\
R & I_s \\
\end{bmatrix}
\end{eqnarray}

ここで，各要素は以下である．

• Qは，ある過渡状態から別の過渡状態に移行する確率を保持するr*r行列である．
• Rは，s*rの行列で，過渡状態から吸収状態に移行する確率を保持する．
• \(0_{r*s}\)は，すべての0のr*s行列である．0は吸収状態から過渡状態（定義上不可能）に移行する確率を表す．
• \(I_s\)は吸収状態間の遷移確率を保持する．遷移は不可能なので，これは単なる\(s*s\)の恒等行列である．

我々は\(\lim_{k \rightarrow \infty} T^k (\mathbf{X}_0)\)に興味がある．

ある与えられたkについて，行列は次のようになる．

\begin{eqnarray}
T^k =
\begin{bmatrix}
Q^k & 0_{r*s} \\
R + RQ + ... + RQ^{k-1} & I_s
\end{bmatrix}
=
\begin{bmatrix}
Q^k & 0_{r*s} \\
R\sum_{i=0}^{k-1}Q_i & I_s \\
\end{bmatrix}
\end{eqnarray}

最後に，吸収マルコフ連鎖の\(T = \begin{bmatrix} Q & 0_{r*s} \\ R & I_s \end{bmatrix}\)を用いると，

\(\lim_{k \rightarrow \infty} T^k = \begin{bmatrix} 0_{r*r} & 0_{r*s} \\ R(I_r - Q)^{-1} & I_s \end{bmatrix} \)になる．

極限では過渡状態への遷移確率はゼロなので，結局は吸収状態に収束し，そこに留まることになる．

ゼロ分散のデータセット（すなわちデルタ関数）を完全に近似できる離散分布の場合，吸収状態はオリジナルの分布から任意の非ゼロ確率点を中心とするデルタ関数になる．

実際には，吸収されるまでの予想ステップ数を知りたい（大きいかもしれないので）．

しかし，我々のフィッティング手順を知らなければ，行列Qを計算することは不可能であり，したがって崩壊するまでの平均的な時間の長さを計算することもできない．

付録A.2：Alternative assumption for noisy approximations（ノイズの多い近似値の代替仮定）

この節では，いくつかの設定によってはより現実的な代替仮定を取り上げる．

4.3節の仮定3とは対照的に，この節は代替というよりむしろ拡張として機能する．

特に，直交性を課す代わりに，ノイズ項に対してある大きさの要求を課すことができる．

これにより同様の結果を得ることができる．

より正確には，4.3節と同じ設定を考えるが，仮定3を仮定3*に置き換える．

仮定：

• 3*：余分なノイズは有界で，標本平均偏差より大きなオーダーであると仮定する．正確には，（生成iに依存しない）定数Kを設定し，すべてのiに対して次が成立する．
  $$ || \varepsilon_{i+1} || \leq \frac{K}{M_i} $$

さて，代替の仮定を置いた上で，まったく同じ計算をすると次のようになる．

$$ \mathbb{E} \left[ R_{W_2}^{i+1} \right] \geq \mathbb{E} ( || \mu_i - \mu ||^2 ) + \frac{Tr \sum}{M_i} + \mathbb{E} ( || \varepsilon_{i+1} ||^2 ) + \frac{2}{\sqrt{M_i}} \mathbb{E} \left( (\varepsilon_{i+1} )^\top \Sigma_i^{1/2} T^{i+1} \right) $$

前回同様，評価する必要がある（今回は代わりに境界を形成する）．

\begin{eqnarray}
\frac{2}{\sqrt{M_i}} \mathbb{E} \left( (\varepsilon_{i+1} )^\top \Sigma_i^{1/2} T^{i+1} \right)
&=& \frac{2}{\sqrt{M_i}} \int d \Sigma_i p(\Sigma_i) Tr \left[ \Sigma_i^{1/2} Cov(\varepsilon_{i+1}, T^{i+1} | \Sigma_i) \right] \neq 0 \\
&\geq& - \frac{2\sqrt{N}}{\sqrt{M_i}} \int d \Sigma_i p(\Sigma_i) \sqrt{Tr [\Sigma_i \Sigma_{\varepsilon_{i+1}}]} \\
&\geq& - \frac{2\sqrt{N}}{\sqrt{M_i}} \sqrt{\mathbb{E} (\varepsilon_{i+1}^\top \Sigma_i \varepsilon_{i+1})} \\
&\geq& - \frac{2\sqrt{N}}{\sqrt{M_i}} \sqrt{\frac{K^2 Tr \Sigma}{M_i^2}} = - \frac{2K\sqrt{N}}{M_i \sqrt{M_i}} \sqrt{Tr \Sigma}
\end{eqnarray}

ここで我々はCauchy-Schwarz不等式とJensen不等式を用いた．

最大の固有値の期待値を使う代わりに，\(Tr \Sigma\)で境界をとったので，これは最適な不等式とはほど遠いことに注意されたい．

特に，1ステップあたりの境界は次のようになる．

$$ \mathbb{E} \left[ R_{W_2}^{i+1} \right] \geq \mathbb{E} ( || \mu_i - \mu ||^2 ) + \frac{Tr \sum}{M_i} + \mathbb{E} ( || \varepsilon_{i+1} ||^2 ) - \frac{2K\sqrt{N}}{M_i \sqrt{M_i}} \sqrt{Tr \Sigma} $$

K，N，\(Tr \Sigma\)の具体的な値についての知識がなければ，\(M_i\)が大きくなるにつれて，これが境界にとってどのような意味を持つかを考えるのが精一杯である．

特に，最後の2つの項からの寄与は最大でも3/2のオーダーとなる．

その結果，これまでに観測されたものと同様の境界が得られる．

$$ \mathbb{E}_{\mu_{n+1}, \sigma_{n+1}^2} \left[ R_{W_2} \right] \geq Tr \Sigma \left( \frac{1}{M_0} + \frac{1}{M_1} + ... + \frac{1}{M_n} \right) + \mathcal{O}(3/2) $$

特に，ステップi + 1での平均が標本平均と最大\(1/M_i\)のオーダーの有界項とに分離できるような，より一般的な近似モデルの場合でも，モデル崩壊の下界を最小化するためには，超線形スケーリングが必要であることを同様に発見する．

参考：The Curse of Recursion: Training on Generated Data Makes Models Forgetの解説動画

The Curse of Recursion: Training on Generated Data Makes Models Forgetの解説動画です．

まとめ

The Curse of Recursion: Training on Generated Data Makes Models Forgetの日本語訳を紹介しました．

大規模言語モデルのモデル崩壊と再帰の呪いがわかりました．

AIのプログラミング言語「C++/Python言語」を学べるおすすめのWebサイトを知りたいあなたはこちらからどうぞ．

独学が難しいあなたは，AIを学べるオンラインプログラミングスクール3社で自分に合うスクールを見つけましょう．後悔はさせません！

国内・海外のAIエンジニアのおすすめ求人サイトを知りたいあなたはこちらからどうぞ．

国内・海外のプロンプトエンジニアのおすすめ求人サイトを知りたいあなたはこちらからどうぞ．