【第7回】元東大教員から学ぶリアルタイムシステム「Rate Monotonicスケジューリング」

こういった私から学べます．

前回を読んでいない方はこちらからどうぞ．

リアルタイムシステムの記事一覧はこちらからどうぞ．

リアルタイムシステムで使われているリアルタイムOSは，主にC言語で書かれています．

私にC言語の無料相談をしたいあなたは，公式LINE「ChishiroのC言語」の友だち追加をお願い致します．

私のキャパシティもあり，一定数に達したら終了しますので，今すぐ追加しましょう！

独学が難しいあなたは，元東大教員がおすすめするC言語を学べるオンラインプログラミングスクール5社で自分に合うスクールを見つけましょう．後悔はさせません！

Rate Monotonic（RM）スケジューリング

Rate Monotonic（RM）スケジューリングは，周期に従ってタスクの優先度を割り当てるシンプルなルールです．

RMは短い周期のタスクに高い優先度を割り当てます．すなわち，周期を優先度に変換します．

周期は一定なので，RMは固定優先度スケジューリングです．

RMでは，タスク\(\tau_i\)の優先度\(P_i\)は実行前に割り当てられて，実行時に変更しません．

さらには，RMはプリエンプティブ（横取り可能）なので，現在実行しているタスクは新しく到着した短い周期（高い優先度）のタスクにプリエンプション（横取り）されます．

Linuxでは，リアルタイムスケジュールポリシー「SCHED_FIFO」を利用することでRMスケジューリングを実装できます．

1973年にLiuとLaylandは，RMが最適であることを証明しました．

最適とは，あらゆる固定優先度スケジューリングでスケジュール可能なタスクセットは，必ずRMもスケジュール可能という意味です．

逆に言うと，RMでスケジュール不可能なタスクセットはあらゆる固定優先度スケジューリングでスケジュール不可能という意味です．

LiuとLaylandは\(n\)個の周期タスクにおけるRMスケジューリングのスケジュール可能上限\(U_{LUB}\)を証明しました．

証明の内容は以下の順番で説明していきます．

• RMの最適性の証明
• RMにおける2タスク向け\(U_{LUB}\)の算出
• RMにおけるnタスク向け\(U_{LUB}\)の算出
• Hyperbolic Boundの算出

RMの最適性の証明

RMスケジューリングの最適性を証明するためには，あるタスクが高優先度タスクと同時にリリースする時はいつでもクリティカルインスタント（タスクの応答時間が最大値になる時刻）になることを示します．

タスクセット\(\Gamma = \{ \tau_1, \tau_2, ..., \tau_n\}\)は，タスクの周期の短い順番にソートされているとします．

すなわち，\(\tau_1\)が一番短い周期（最高優先度），\(\tau_n\)が一番長い周期（最低優先度）になります．

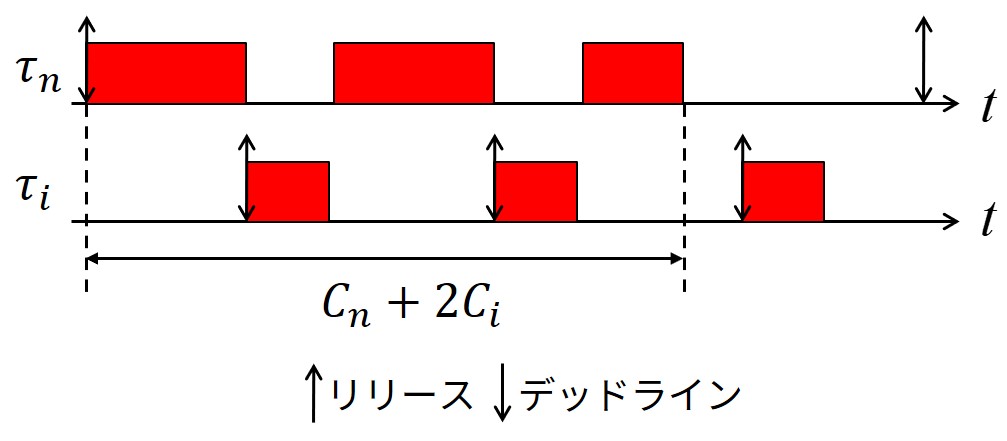
下図に示すように，タスク\(\tau_i (i<n)\)がタスク\(\tau_n\)の実行中にリリースすると，プリエンプションして実行します．

タスク\(\tau_n\)の応答時間は高優先度タスク\(\tau_i\)の干渉（Interference）により遅延します．

この場合は，タスク\(\tau_i\)はタスク\(\tau_n\)の実行を2回（\(2C_i\)）干渉しています．

なので，タスク\(\tau_n\)の応答時間は\(C_n + 2C_i\)になります．

また，下図に示すように，タスク\(\tau_i\)がタスク\(\tau_n\)を干渉することで，\(\tau_n\)の終了時刻が長くなります．

この場合は，タスク\(\tau_i\)はタスク\(\tau_n\)の実行を3回（\(3C_i\)）干渉しています．

なので，タスク\(\tau_n\)の応答時間は\(C_n + 3C_i\)になります．

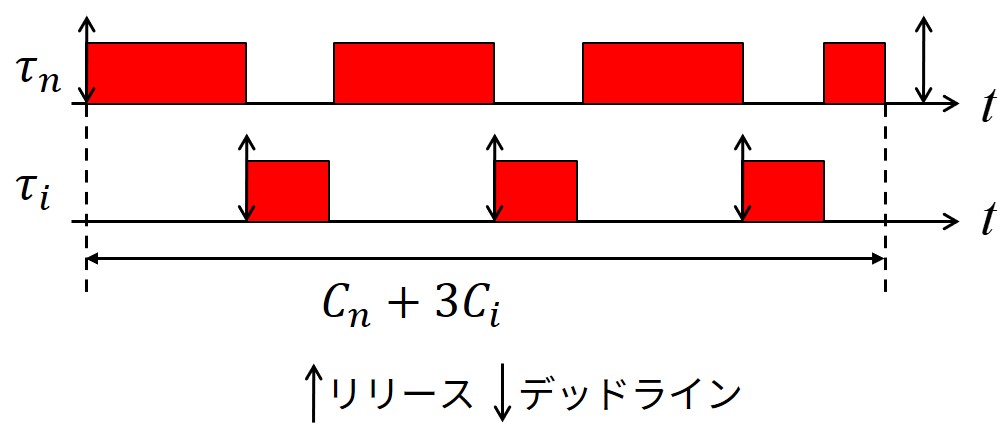
結果として，タスク\(\tau_n\)の応答時間は高優先度タスク\(\tau_i\)と同時にリリースした時に最大になります．

全てのタスク\(\tau_i (i=１, ..., n-1)\)の応答時間を算出することで，タスクの最悪応答時間は全ての高優先度タスクが同時にリリースした時になることを証明します．

この結果の最初の帰着は，タスクのスケジュール可能性はクリティカルインスタントで簡単にチェックできることです．

具体的には，全てのタスクがクリティカルインスタントでスケジュール可能であれば，タスクセットは他の場合でもスケジュール可能です．

タスクセットが任意の優先度で割り当てたタスクセットがスケジュール可能であれば，RMでのスケジュール可能であることを示すことで，RMの最適性が正しいことがわかります．

2つの周期タスク\(\tau_1\)と\(\tau_2\)があり，それぞれの周期の関係は\(T_1 < T_2\)とします．

もしRMのように優先度を割り当てない場合は，タスク\(\tau_2\)が最高優先度になります．

この状況は下図で示すように，クリティカルインスタントで以下の数式を満たす場合にスケジュール可能になります．

$$C_1 + C_2 \leq T_1 \tag{7.1}$$

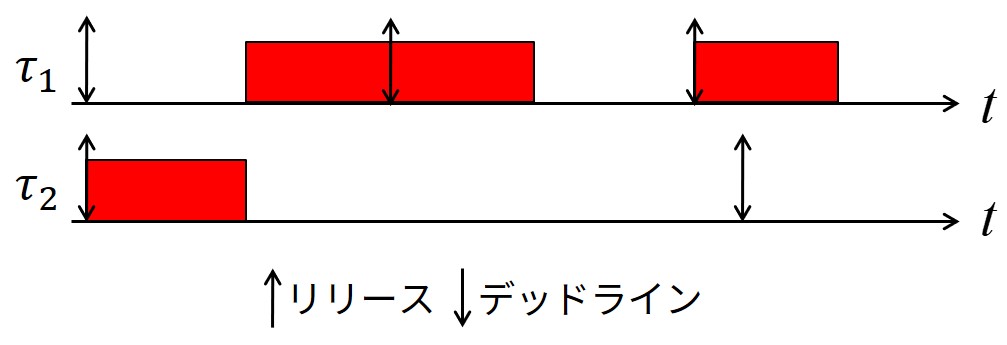
他方，優先度がRMで割り当てられる場合，タスク\(\tau_1\)は最高優先度になります．

この状況でスケジュール可能であることを保証するためには，以下の2つのケースを考えなければなりません（下図）．

\(F=\lfloor T_2 / T_1 \rfloor\)をタスク\(T_2\)に含まれる\(\tau_1\)の周期の数と置きます．

※\(\lfloor x \rfloor\)は\(x\)以下の最大の整数を表し，\(\lceil x \rceil\)は\(x\)以上の最大の整数を表します．

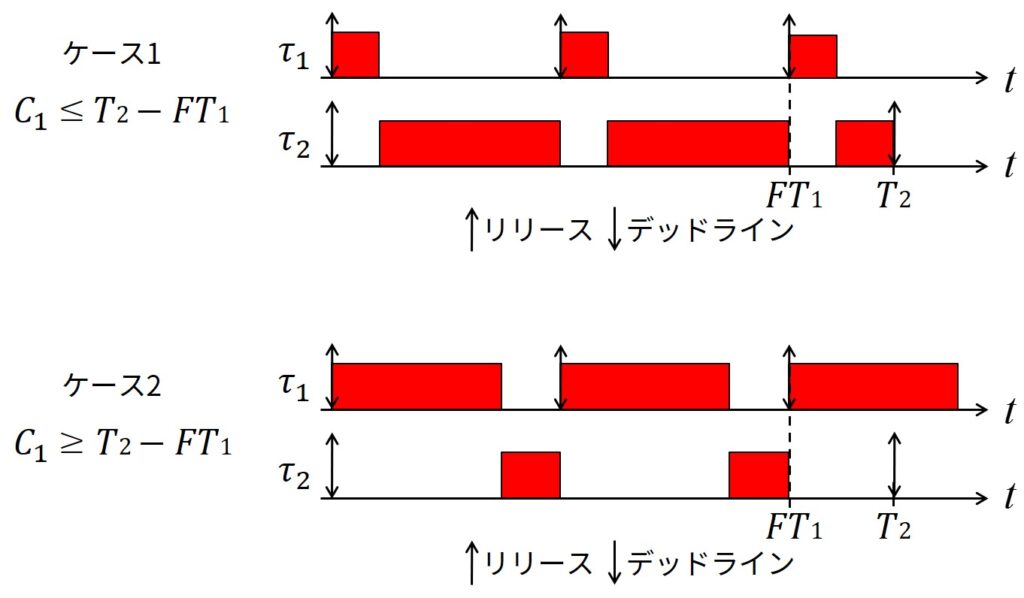
ケース1：\(C_1 \leq T_2 - FT_1\)が成立する場合

（タスク\(\tau_2\)と同期して起動する）タスク\(\tau_1\)の最悪実行時間が，タスク\(\tau_2\)の2番目のジョブのリリースまでに終了する程度に十分短い場合を考えます．

このケースでは，タスクセットは下式を満たす場合にスケジュール可能です．

$$(F+1)C_1 + C_2 \leq T_2 \tag{7.2}$$

これから，式\((7.1)\)は式\((7.2)\)を含むことを示します．

式\((7.1)\)の両辺に\(F\)を掛けると下式になります．

$$FC_1 + FC_2 \leq FT_1$$

\(F \leq 1\)なので，下式に展開できます．

$$FC_1 + C_2 \leq FC_1 + FC_2 \leq FT_1$$

\(C_1\)を上式の一番左と一番右の数式に追加すると以下になります．

$$(F+1)C_1 + C_2 \leq FT_1 + C_1$$

\(C_1 < T_2 - FT_1\)を想定していたので，下式が成立します．

$$(F+1)C_1 + C_2 \leq FT_1 + C_1 \leq T_2$$

したがって，式\((7.2)\)が成立します．

ケース2：\(C_1 \geq T_2 - FT_1\)が成立する場合

（タスク\(\tau_2\)と同期して起動する）タスク\(\tau_1\)の最悪実行時間が，タスク\(\tau_2\)の2番目のジョブのリリースに重なる程度に十分長い場合を考えます．

このケースでは，タスクセットは下式を満たす場合にスケジュール可能です．

$$FC_1 + C_2 \leq FT_1 \tag{7.3}$$

ケース1と同様に式\((7.1)\)は式\((7.3)\)を含むことを示します．

式\((7.1)\)の両辺に\(F\)を掛けると下式になります．

$$FC_1 + FC_2 \leq FT_1$$

\(F \geq 1\)なので，下式に展開できます．

$$FC_1 + C_2 \leq FC_1 + FC_2 \leq FT_1$$

この式は式\((7.3)\)を満たします．

ケース1とケース2のまとめとRMの最適性の算出

基本的には，2つの周期タスク\(\tau_1\)と\(\tau_2\)が\(T_1 < T_2\)を満たす場合，もし任意の優先度割り当てでスケジュール可能であればRMでもスケジュール可能です．

すなわち，RMは最適です．

この結果は簡単に\(n\)個の周期タスクに拡張できます．

RMスケジューリングにおいてCPU利用率のスケジュール可能上限\(U_{lub}\)を算出する方法を示します．

この上限は，まずに2タスクの場合を示し，次に\(n\)タスク（任意の数のタスク）の場合に拡張します．

RMにおける2タスク向け\(U_{LUB}\)の算出

2つの周期タスク\(\tau_1\)と\(\tau_2\)が\(T_1 < T_2\)を満たす場合を考えます．

RMのスケジュール可能上限\(U_{lub}\)を算出するために以下を満たさなければなりません．

• RMでタスクに優先度を割り当てます．すなわち，タスク\(\tau_1\)が最高優先度になります．
• CPUを計算時間でフル活用することで，タスクセットの上限\(U_{ub}\)を算出します．
• 全ての他のタスクのパラメータに関して上限\(U_{ub}\)を最小化します．

以前に，\(F=\lfloor T_2 / T_1 \rfloor\)をタスク\(\tau_2\)周期\(T_2\)に含まれる\(\tau_1\)の周期\(T_1\)の数と置きました．

一般性を失うことなく，最悪実行時間\(C_2\)はCPUをフル活用するように調整します．

前回と同様に，2つのケースを考えます．

ケース1：\(C_1 \leq T_2 - FT_1\)が成立する場合

（タスク\(\tau_2\)と同期して起動する）タスク\(\tau_1\)の最悪実行時間が，タスク\(\tau_2\)の2番目のジョブのリリースまでに終了する程度に十分短い場合を考えます．

このケースでは，\(C_2\)の最大値は下式になります．

$$C_2 = T_2 - C_1 (F + 1)$$

この場合の上限\(U_{ub}\)は下式になります．

\begin{eqnarray}
U_{ub} &=& \frac{C_1}{T_1} + \frac{C_2}{T_2} = \frac{C_1}{T_1} + \frac{T_2 - C_1 (F + 1)}{T_2} \\
&=& 1 + \frac{C_1}{T_1} - \frac{C_1}{T_2}(F + 1) \\
&=& 1 + \frac{C_1}{T_2} \left[ \frac{T_2}{T_1} - (F + 1) \right]
\end{eqnarray}

大括弧の値\([T_2/T_1 - (F+1)]\)は負なので，上限\(U_{ub}\)は\(C_1\)において単調減少になります．

\(C_1 \leq T_2 - FT_1\)なので，上限\(U_{ub}\)の最小値は下式になります．

$$C_1 = T_2 - FT_1$$

ケース2：\(C_1 \geq T_2 - FT_1\)が成立する場合

（タスク\(\tau_2\)と同期して起動する）タスク\(\tau_1\)の最悪実行時間が，タスク\(\tau_2\)の2番目のジョブのリリースに重なる程度に十分長い場合を考えます．

このケースでは，\(C_2\)の最大値は下式になります．

$$C_2 = (T_1 - C_1)F$$

この場合の上限\(U_{ub}\)は下式になります．

\begin{eqnarray}
U_{ub} &=& \frac{C_1}{T_1} + \frac{C_2}{T_2} = \frac{(T_1 - C_1)F}{T_2} \\
&=& \frac{T_1}{T_2}F + \frac{C_1}{T_1} - \frac{C_1}{T_2}F \\
&=& \frac{T_1}{T_2}F + \frac{C_1}{T_2} \left[ \frac{T_2}{T_1} - F \tag{7.4} \right]
\end{eqnarray}

大括弧の値\([T_2/T_1 - F]\)は負なので，上限\(U_{ub}\)は\(C_1\)において単調減少になります．

\(C_1 \geq T_2 - FT_1\)なので，上限\(U_{ub}\)の最小値は下式になります．

$$C_1 = T_2 - FT_1$$

ケース1とケース2のまとめとスケジュール可能上限の算出

したがって，両方のケースで上限\(U_{ub}\)の最小値は下式になります．

$$C_1 = T_2 - FT_1$$

\(C_1\)の最小値は式\((7.4)\)から下式になります．

\begin{eqnarray}
U &=& \frac{T_1}{T_2}F + \frac{C_1}{T_2} \left( \frac{T_2}{T_1} - F \right) \\
&=& \frac{T_1}{T_2}F + \frac{(T_2 - T_1 F)}{T_2} \left( \frac{T_2}{T_1} - F \right) \\
&=& \frac{T_1}{T_2} \left[ F + \left( \frac{T_2}{T_1} - F \right) \left( \frac{T_2}{T_1} - F \right) \right] \tag{7.5}
\end{eqnarray}

表記を簡略化するために，\(G=T_2/T_1 - F \)と置きます．

\begin{eqnarray}
U &=& \frac{T_1}{T_2} (F + G^2) = \frac{(F + G^2)}{T_2 / T_1} \\
&=& \frac{(F + G^2)}{(T_2 / T_1 - F) + F} = \frac{F + G^2}{F + G} \\
&=& \frac{(F + G) - (G - G^2)}{F + G} = 1 - \frac{G (1 - G)}{F + G} \tag{7.6}
\end{eqnarray}

\(0 \leq G < 1\)なので，\(G (1 - G)\)は非負であることがわかります．

\(U\)は\(F\)が大きくなると単調増加します．

結果として，\(U\)の最小値は\(F\)の最小値の時，つまり\(F=1\)の時になります．

\begin{eqnarray}
U &=& \frac{1 + G^2}{1 + G} \tag{7.7}
\end{eqnarray}

\(G\)に対する\(U\)の最小値を算出するために，偏微分します．

※偏微分の分数の公式は下式になりますので，こちらを見ながら式展開を理解して下さい．

$$\left( \frac{\partial f}{\partial x} \right)' = \frac{f'x - x'f}{x^2}$$

それでは，偏微分しましょう．

\begin{eqnarray}
\frac{\partial U}{\partial G} &=& \frac{2G(1 + G) - (1 + G^2)}{(1 + G)^2} \\
&=& \frac{G^2 + 2G - 1}{(1 + G)^2}
\end{eqnarray}

\(G^2 + 2G - 1 = 0\)の時，\(\partial U / \partial G = 0\)になりますので，以下の2つの解があります．

\begin{cases}
G_1 &=& -1 - \sqrt{2} \\
G_2 &=& -1 + \sqrt{2}
\end{cases}

\(0 \leq G < 1\)なので，負の値である\(G = G_1\)は除外されます．

\(U\)のスケジュール上限は\(G=G_2\)の時とわかります．

それでは，式\((7.7)\)に\(G=G_2\)を代入しましょう．

$$U_{lub} = \frac{1 + (\sqrt{2} - 1)^2}{1 + (\sqrt{2} - 1)} = \frac{4 - 2 \sqrt{2}}{\sqrt{2}} = 2 (\sqrt{2} - 1)$$

すなわち，\(U_{lub}\)は下式になります．

$$U_{lub} = 2 (2^{1/2} - 1) \simeq 0.828 \tag{7.8}$$

もし\(T_2\)が\(T_1\)の倍数であれば，\(G=0\)になり，式\((7.7)\)からスケジュール可能上限は1になります．

一般的には，2タスク向けスケジュール可能上限は比率\(k=T_2/T_1\)により計算することができます．

\(F\)において，式\((7.5)\)から下式になります．

$$U = \frac{F + (k - F)^2}{k} = k - 2F + \frac{F (F + 1)}{k} $$

\(k\)に対して\(U\)の最小値を算出するために，偏微分します．

$$\frac{\partial U}{\partial k} = 1 - \frac{F (F + 1)}{k^2}$$

\(k^* = \sqrt{F (F + 1)}\)の時，\(\partial U / \partial k = 0\)になります．

\(F\)において，\(U\)の最小値は下式になります．

$$U^* = 2(\sqrt{F ( F + 1)} - F)$$

下表に\(F\)を関数とした\(k^*\)と\(U^*\)の値を示します．

\(F\)	\(k^*\)	\(U^*\)
\(1\)	\(\sqrt{2}\)	\(0.828\)
\(2\)	\(\sqrt{6}\)	\(0.899\)
\(3\)	\(\sqrt{12}\)	\(0.928\)
\(4\)	\(\sqrt{20}\)	\(0.944\)
\(5\)	\(\sqrt{30}\)	\(0.954\)

下図に\(k\)に対する\(U\)の上限を示します．

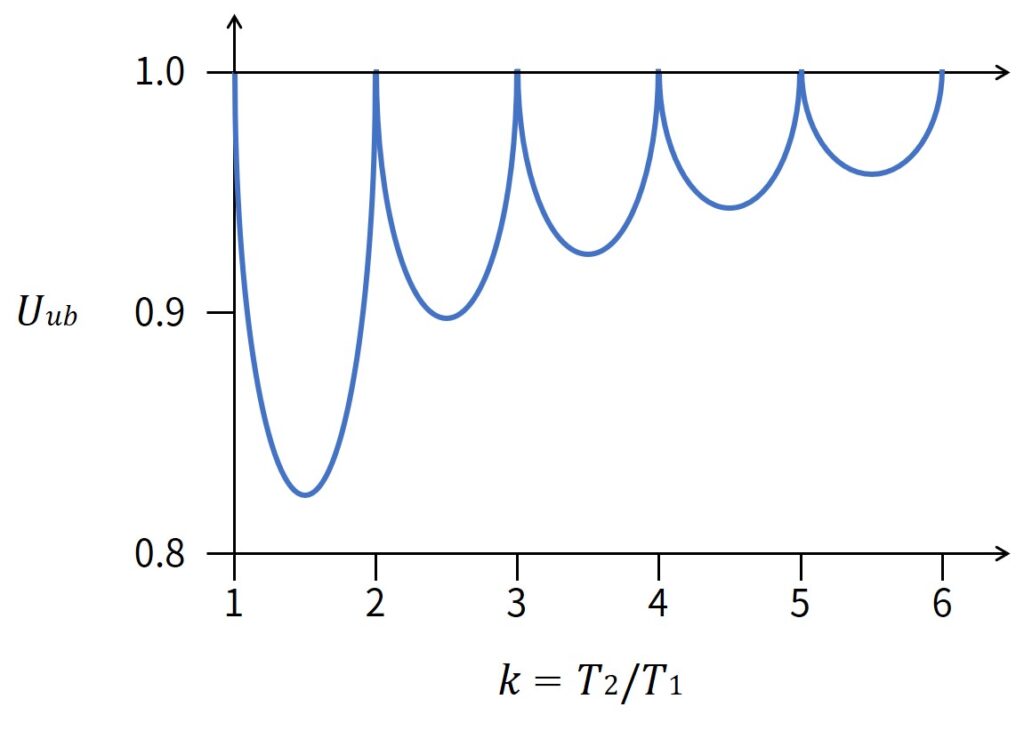
RMにおける\(n\)タスク向け\(U_{LUB}\)の算出

前章での算出で，スケジュール可能上限の条件は下式になります．

\begin{cases}
F &=& 1 \\
C_1 &=& T_2 - FT_1 \\
C_2 &=& (T_1 - C_1) F
\end{cases}

上式は，下式のように書き換えられます．

\begin{cases}
T_1 &<& T_2 < 2T_1 \\
C_1 &=& T_2 - T_1 \\
C_2 &=& 2T_1 - T_2
\end{cases}

任意の\(n\)タスクのセットを一般化するために，CPUをフル活用するタスクセットのスケジュール可能性の最悪条件は下式になります．

\begin{cases}
T_1 &<& T_n < 2T_1 \\
C_1 &=& T_2 - T_1 \\
C_2 &=& T_3 - T_2 \\
... \\
C_{n-1} &=& T_n - T_{n-1} \\
C_n &=& T_1 - (C_1 + C_2 + ... + C_{n-1}) = 2T_1 - T_n
\end{cases}

タスクセットのCPU利用率は下式になります．

$$U = \frac{T_2 - T_1}{T_1} + \frac{T_3 - T_2}{T_2} + ... + \frac{T_n - T_{n-1}}{T_{n-1}} + \frac{2T_1 - T_n}{T_n}$$

\(R_i=T_{i+1}/T_i\)と置くと，下式が算出されます．

$$R_1 R_2 ... R_{n-1} = \frac{T_n}{T_1}$$

CPU利用率は下式のように書き換えられます．

$$U = \sum_{i=1}^{n-1} R_i + \frac{2}{R_1 R_2 ... R_{n-1}} - n$$

\(R_i (i = 1, ..., n - 1)\)に対して\(U\)の最小値を算出するために，偏微分します．

$$\frac{\partial U}{\partial R_k} = 1 - \frac{2}{R_i^2 \left( \prod_{i \neq k}^{n-1} R_i \right)}$$

\(P = R_1 R_2 ... R_{n-1}\)と定義すると，\(U\)は以下の時に最小値になります．

\begin{cases}
R_1 P &=& 2 \\
R_2 P &=& 2 \\
... \\
R_{n-1} P &=& 2
\end{cases}

すなわち，全ての\(R_i\)が同じ値を持つ下式になります．

$$R_1 = R_2 = ... = R_{n-1} = 2^{1/n}$$

上記の値を\(U\)の式に置換すると下式になります．

\begin{eqnarray}
U_{lub} &=& (n - 1) 2^{1/n} + \frac{2}{2^{(1 - 1/n)}} - n \\
&=& n 2^{1/n} - 2^{1/n} + 2^{1/n} - n \\
&=& n (2^{1/n} - 1)
\end{eqnarray}

したがって，周期タスクの任意のセットで，RMスケジューリングのスケジュール可能上限は下式になります．

$$U_{lub} = n (2^{1/n} - 1) \tag{7.9} $$

\(n\)が大きくなるほどスケジュール可能上限\(U_{lub}\)は小さくになります．

下表に\(n=1, 2, 3, ..., 10\)の\(U_{lub}\)を記載します．

\(n\)	\(U_{lub}\)
\(1\)	\(1.000\)
\(2\)	\(0.828\)
\(3\)	\(0.780\)
\(4\)	\(0.757\)
\(5\)	\(0.743\)
\(6\)	\(0.735\)
\(7\)	\(0.729\)
\(8\)	\(0.724\)
\(9\)	\(0.721\)
\(10\)	\(0.718\)

\(n\)が大きくなるとスケジュール可能上限は以下に収束します．

$$U_{lub} = \ln{2} \simeq 0.693$$

上式を\(y = (2^{1/n} - 1)\)で置換すると，\(n = \frac{\ln{2}}{\ln{(y + 1)}}\)により，下式になります．

$$ \lim_{n \to \infty} n (2^{1/n} - 1) = (\ln{2}) \lim_{y \to 0} \frac{y}{(y+1)} $$

ロピタルの定理を使うと下式になります．

$$ \lim_{y \to 0} \frac{y}{\ln{(y+1)}} = \lim_{y \to 0} \frac{1}{1/(y+1)} = \lim_{y \to 0} (y + 1) = 1$$

したがって，スケジュール可能上限は下式になります．

$$ \lim_{n \to \infty} U_{lub} (n) = \ln{2} $$

ハーモニックな周期タスクセットのRMにおける\(n\)タスク向け\(U_{LUB}\)の算出

ハーモニックな周期タスクセットとは，タスクの周期がハーモニックの関係（タスクの長い周期が短い周期の整数倍）になることです．

ハーモニックな周期タスクセットの周期の例は以下になります．

• 周期タスクセット1：1ms，5ms，10ms，50ms，100ms，500ms，1000ms，．．．
• 周期タスクセット2：1ms，2ms，4ms，8ms，16ms，32ms，64ms，128ms，．．．

ハーモニックな周期タスクセットにおけるRMにおける\(n\)タスク向けスケジュール可能上限\(U_{LUB}\)は下式になります．

$$ U_{lub} (n) = 1 $$

なぜスケジュール可能上限が\(U_{lub} (n) = 1\)になるのかを簡単に説明します．

まず，2タスクでハーモニックの関係の場合，\(k = T_2 / T_1\)が必ず整数になります．

先述した「kに対するUの上限」を示す図を見ると，kが整数の場合は\(U_{ub}\)が必ず1になっていることがわかります．

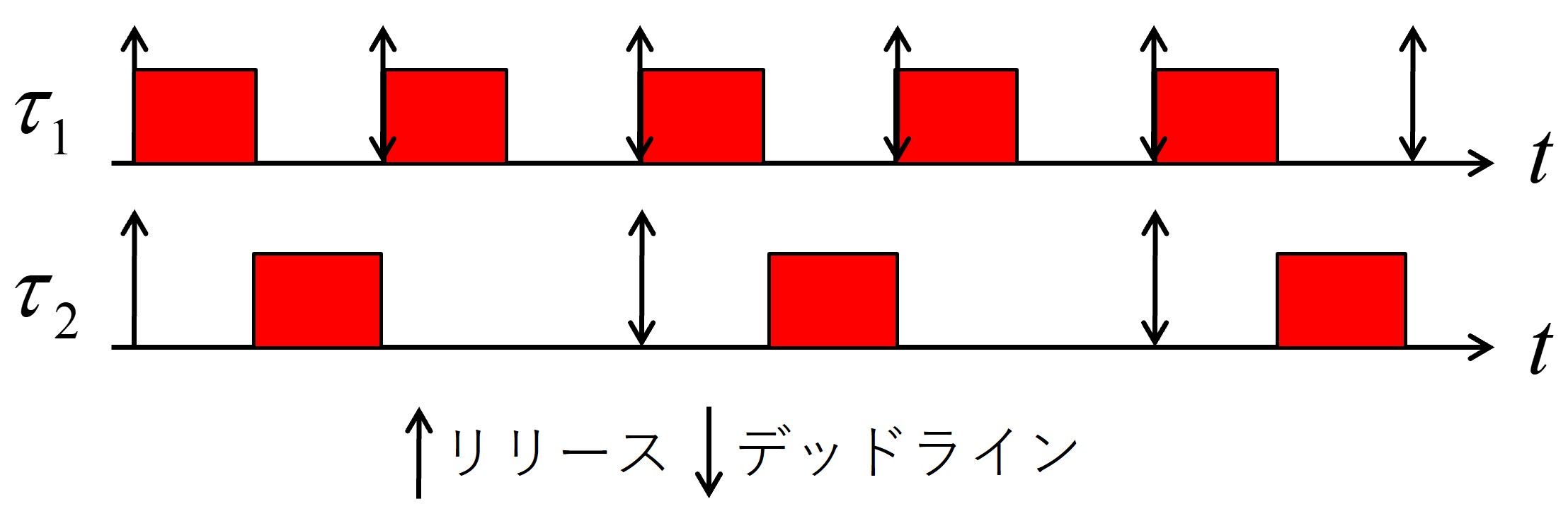
タスク\(\tau_2\)の周期がタスク\(\tau_1\)の周期の2倍のスケジュール例は上図になります．

タスク\(\tau_2\)の周期がタスク\(\tau_1\)の周期の整数倍になるため，タスク\(\tau_2\)はリリース時に実行を開始できません．

また，タスク\(\tau_1\)の実行が終了した後に，必ずタスク\(\tau_2\)は実行を開始します．

つまり，ハーモニックな周期タスクセットの場合は，全タスクの毎周期ごとに必ず同じスケジュールを繰り返します．

もしタスク\(\tau_2\)の実行時間を長くしてCPU利用率が100%になった場合でも，デッドラインミスは発生しません．

上記の関係が\(n\)タスクの場合でも成立するため，ハーモニックな周期タスクセットにおけるRMのスケジュール可能上限は\(U_{lub} (n) = 1\)になります．

Hyperbolic Boundの算出

RMのスケジュール可能性解析は，Hyperbolic Boundと呼ばれる他の方法でも算出できます．

Hyperbolic Boundの解析は，オリジナルのLiuとLaylandの解析と同じ計算量を持ちつつ，オリジナルでスケジュール不可能と判定されたタスクセットをスケジュール可能と判定できます．

タスクの周期に関連してCPU利用率を最小化する代わりに，各々のタスクのCPU利用率を利用することで，より厳密な十分条件のスケジュール可能性判定をすることができます．

以下の定理がRMのスケジュール可能性判定のテストの十分条件になります．

Hyperbolic Boundの定理

定理7.1：\(\Gamma = \{ \tau_1, ..., \tau_n \}\)を\(n\)個の周期タスクを持つタスクセット，各々のタスク\(\tau_i\)のCPU利用率を\(U_i\)と置く．\(\Gamma\)はRMで以下の条件を満たせばスケジュール可能になる．

$$ \prod_{i=1}^n (U_i + 1) \leq 2 \tag{7.10} $$

証明：一般性を失わずに，タスクは周期の短い順にソートされているとします．

すなわち，\(\tau_1\)が最高優先度で\(\tau_n\)が最低優先度になります．

LiuとLaylandの証明では，\(n\)個の周期タスクの最悪の状況は，全てのタスクが同時に起動し（例：\(t = 0\)），周期が以下の関係になることです．

$$ \forall i = 2, ..., n \ \ T_1 < T_i < 2T_1$$

さらには，最悪実行時間が以下の関係になる時に，合計のCPU利用率が最小値になります．

\begin{cases}
C_1 &=& T_2 - T_1 \\
C_2 &=& T_3 - T_2 \\
... \\
C_{n-1} &=& T_n - T_{n-1} \tag{7.11}
\end{cases}

スケジュール可能性判定は下式になります．

$$ \sum_{i=1}^n C_i \leq T_1 \tag{7.12}$$

式\((7-11)\)より，スケジュール可能性判定は下式のように書き換えられます．

$$ C_n \leq 2 T_1 - T_n \tag{7.13}$$

\(R_i=T_{i+1}/T_i\)，\(U_i=C_i/T_i\)と置くと，式\((7.11)\)は下式のように書き換えられます．

\begin{cases}
U_1 &=& R_1 - 1 \\
U_2 &=& R_2 - 1 \\
... \\
U_{n-1} &=& R_{n-1} - 1 \tag{7.14}
\end{cases}

また，以下が成立することを発見しました．

$$ \prod_{i=1}^{n-1} R_i = \frac{T_2}{T_1} \frac{T_3}{T_2} ... \frac{T_n}{T_{n-1}} = \frac{T_n}{T_1} $$

式\((7.13)\)を\(T_n\)で割ると下式になります．

$$ U_n \leq \frac{2T_1}{T_n} - 1$$

CPUをフル活用するタスクセットのスケジュール可能性判定は下式に書き換えられます．

$$ U_n + 1 \leq \frac{2}{\prod_{i=1}^{n-1} R_i} $$

全ての\(i = 1, ..., n\)において\(R_i = U_i + 1\)なので，下式が成立します．

$$ (U_n + 1) \prod_{i=1}^{n-1} (U_i + 1) \leq 2$$

したがって，下式が成立します．

$$ \prod_{i=1}^n (U_i + 1) \leq 2$$

□

Hyperbolic BoundテストとLiuとLaylandのテストの比較

Hyperbolic BoundテストとLiuとLaylandのテストをタスクの利用率の空間「U-space」で比較します．

RMにおけるLiuとLaylandのテストは\(n\)次元の平面で表され，各々の軸は\(U_{lub} (n) = n (2^{1/n} - 1)\)で交差します．

RM表面以下の全てのポイントはRMでスケジュール可能な周期タスクセットを表します．

式\((7.10)\)のHyperbolic Boundは，RMに対する\(n\)次元の双曲線（Hyperbolic）の表面の正接（Tangent）として表現され，\(U_i = 1\)で軸が交差します（これがHyperbolic Boundと呼ばれる理由です）．

下図に\(n=2\)の場合のHyperbolic Boundを示します．

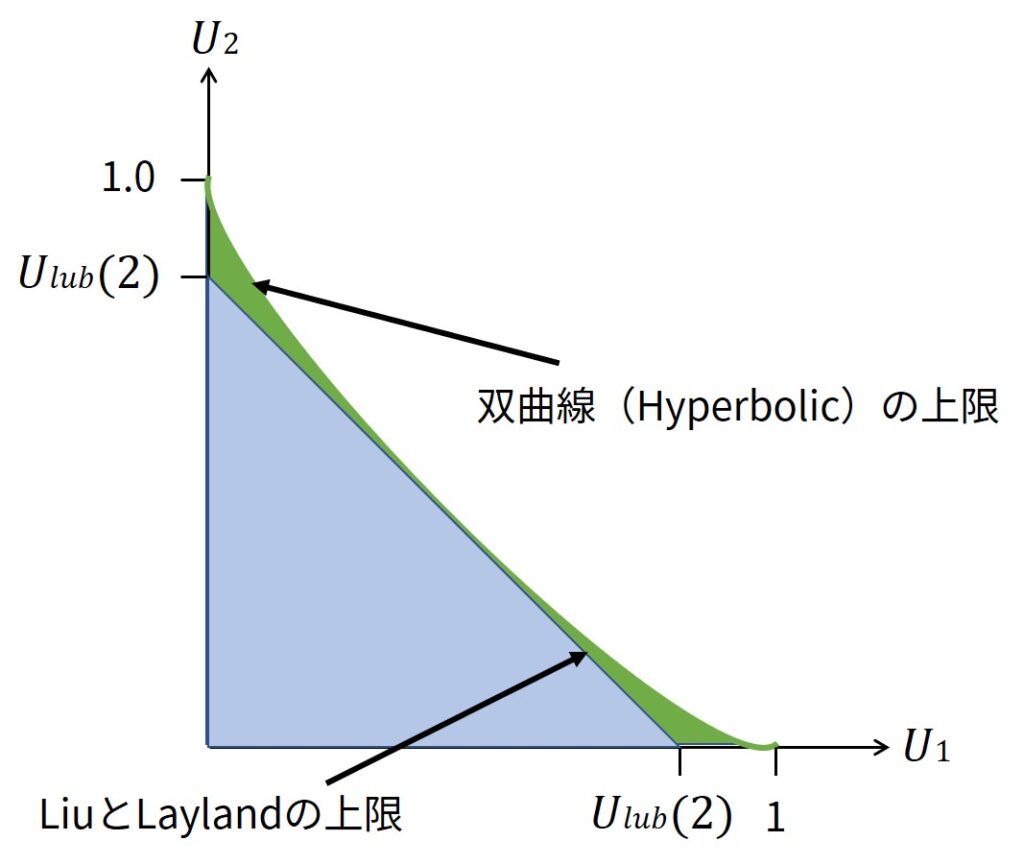
双曲線の漸近線は\(U_i = -1\)になります．

このプロットから，Hyperbolic Bound以下のスケジュール可能な領域は，LiuとLaylandの上限より大きいことがわかります．

Hyperbolic Boundは厳密です．つまり，もし満たせないならば，これらのCPU利用率においてタスクセットがスケジュール不可能です．

したがって，Hyperbolic Boundはタスクセットの情報として各々のタスクのCPU利用率\(U_i\)を知っているという条件では，一番高い可能性があるテストです．

HyperbolicテストのLiuとLaylandのテストに対するスケジュール可能性の増加分は，タスク数が増えるほど大きくなります．

タスク数\(n\)が無限大（∞）になると，スケジュール可能性の増加分は\(\sqrt{2}\)になります．

まとめ

今回は，Rate Monotonic（RM）スケジューリングを解説しました．

具体的には，以下の内容を解説しました．

• RMは周期の短いタスクに高い優先度を割り当て
• RMは最適な固定優先度スケジューリング
• RMのスケジュール可能上限\(U_{lub} = n (2^{1/n} - 1)\)

RMは代表的なリアルタイムスケジューリングなので是非きちんと理解しましょう！

次回は，RMと並んで代表的なスケジューリング「Earliest Deadline First（EDF）」を紹介します．

リアルタイムシステムで使われているリアルタイムOSは，主にC言語で書かれています．

私にC言語の無料相談をしたいあなたは，公式LINE「ChishiroのC言語」の友だち追加をお願い致します．

私のキャパシティもあり，一定数に達したら終了しますので，今すぐ追加しましょう！

独学が難しいあなたは，元東大教員がおすすめするC言語を学べるオンラインプログラミングスクール5社で自分に合うスクールを見つけましょう．後悔はさせません！

次回はこちらからどうぞ．